2.5.2 Методи підвищення точності автоматичного регулювання

До загальних методів підвищення точності відносять:

• підвищення коефіцієнта підсилення розімкнутого кола – є найбільш універсальним і ефективним методом. На практиці це досягається за рахунок введення підсилювачів. Підвищення коефіцієнта призводить до зменшення похибки в усіх типових режимах (коефіцієнт входить в знаменник розрахункових виразів). Проте підвищення обмежується стійкістю системи. При підвищенні коефіцієнта система наближається до межі стійкості. Це призводить до необхідності розробки коректуючи пристроїв;

• підвищення порядку астатизму – формально це зводиться до приведення до нуля перших коефіцієнтів похибок системи. На практиці – здійсненням вводу інтегруючих кіл;

• застосування регулювання за похідною від похибки – здійснюється вводом диференційних ланок.

Під поняттям покращення якості процесу регулювання, розуміють зміну динамічних властивостей системи регулювання з метою отримання необхідного запасу стійкості та швидкодії. При вирішенні задачі підвищення запасу стійкості спочатку намагаються змінити параметри окремих ланок. Якщо не вдається в рамках системи досягти бажаних результатів – змінюють її структуру: вводять коректуючи засоби, дія яких аналогічна введенню в закон регулювання похідних або інтегралів.

Введення похідної в закон регулювання.

П – підсилювач; КО – керуючий орган;

Д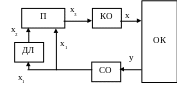 Л – диференційна ланка; СО – сприймаючий орган; ОК – об’єкт керування.

Сигнал на виході диференційної ланки x₂=kdx₁/dt. Сприймаючий орган подає на входи ДЛ та П сигнал x₁=k₁y. На П поступає сумарний сигнал x₃=k₂(x₁ –x₂).

КО діє на ОК x=k₃x₃. Тоді закон регулювання буде:

де k=k₁k₂k₃ – загальний передаточний коефіцієнт.

Таким чином, зміна регулюючої дії x на ОК залежить не тільки від відхилення керуючої величини, але й від швидкості цього відхилення dy/dt, тобто в цей закон регулювання введена похідна.

Введення похідної призводить до зменшення амплітуди та довжини коливань перехідного процесу. Якщо регулятор пропорціональної дії (y=k_px), то до тих пір доки y  0, регулятор зменшує позитивне відхилення. При y  0 регулювання буде діяти в зворотному напрямку.

І з-за інерційності системи напрямок дії регулятора змінюється не в точці b, а на ділянці bc. Спостерігається розкачування системи, що буде тим більше, чим більший коефіцієнт підсилення системи.

Якщо в системі введена диференційна ланки, то при позитивній дії y, dy/dt також має позитивний знак. Сумарна дія x₁+x₂ підсилює дію регулятора на зменшення відхилення у. Зміна вихідної величини має аперіодичний характер – лінія оа’ (штрих-пунктир).

Сигнал за похідною dy/dt збільшує затухання коливань, а сигнал за відхиленням у – зменшує статичну похибку.

Введення інтеграла в закон регулювання.

Дозволяє отримати астатичну систему (=0). Закон регулювання буде:

І нтеграл визначає площу під кривою зміни відхилення величини, що регулюється. Звідси інтегруюча ланка, як корекція, здійснює вплив головним чином в кінці перехідного процесу і ліквідує статичну похибку в усталеному режимі. Введення інтегруючої ланки в коливальну систему, в противагу аперіодичній системі, може призвести до збільшення її коливальності (bc’) і привести до нестійкості .

Для покращення якості регулювання застосовують комбінаційні послідовні коректуючи пристрої, що складаються з диференційної та інтегральної ланок. В цьому випадку диференційна ланка зменшує схильність системи до коливань, а інтегруюча – зменшує статичну похибку. (Іншими словами, похідна покращує процес регулювання в перехідному режимі, а інтеграл – в статичному).