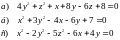- •Вариант I
- •Вариант II
- •А. Исследовать и решить систему уравнений:
- •Найти собственные значения и собственные векторы матрицы:
- •Показать, что векторы образуют базис и найти координаты вектора в этом базисе.
- •Вариант III
- •Вариант IV
- •Вариант V
- •Вариант VI
- •Вариант VII
- •Вариант VIII
- •Вариант IX
- •Вариант X
- •Вариант XI
- •Вариант XII
- •Вариант XIII
- •Вариант XIV
- •Вариант XV
- •Вариант XVI
- •Вариант XVII
- •Вариант XVIII
- •Вариант XIX
- •Вариант XX
Вариант I
а. Исследовать и решить систему уравнений:
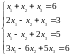
б. Найти
фундаментальную систему решений:

с. Решить
матричное уравнение:
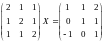
Найти собственные значения и собственные векторы матрицы:
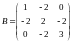
Показать, что векторы
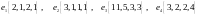 образуют базис и найти координаты
вектора
образуют базис и найти координаты
вектора
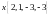 в этом базисе.
в этом базисе.а. Найти ортогональную проекцию вектора
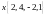 на подпространство, натянутого на
векторы:
на подпространство, натянутого на
векторы:
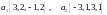 .
.
б. Найти матрицу линейного
преобразования (в базисе, в котором
заданы координаты всех векторов),
переводящего векторы
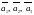 ,
в векторы
,
в векторы
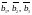 соответственно:
соответственно:
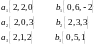
Найти расстояние от вектора до подпространства, натянутого на систему векторов
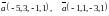 .
.
1. Найти ортогональное преобразование, приводящее квадратичную форму
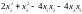 к каноническому виду и написать этот
канонический вид.
к каноническому виду и написать этот
канонический вид.
2. Определить форму, размеры и расположение поверхностей заданных уравнениями:
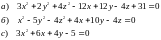
Вариант II
А. Исследовать и решить систему уравнений:
б. Найти
фундаментальную систему решений:
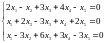
с. Решить
матричное уравнение:
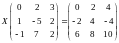
Найти собственные значения и собственные векторы матрицы:
Показать, что векторы образуют базис и найти координаты вектора в этом базисе.
а. Ортогонализовать и дополнить до ортонормированного базис
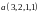 ,
,
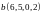 ,
,
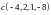 .
.
б. Найти матрицу линейного
преобразования, переводящего векторы
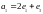 ,
,
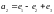 ,
,
 соответственно в векторы
соответственно в векторы
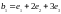 ,
,
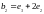 ,
,
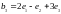 .
.
Найти угол между вектором
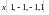 и подпространством, натянутым на векторы
и подпространством, натянутым на векторы
 и
и
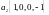 .
.
1. Найти ортогональное преобразование, приводящее квадратичную форму
 к каноническому виду. Выписать
канонический вид формы.
к каноническому виду. Выписать
канонический вид формы.
2. Определить вид, размеры и расположение поверхностей заданных уравнениями:

Вариант III
а. Исследовать и решить систему уравнений:
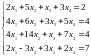
б. Найти
фундаментальную систему решений:
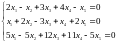
с. Решить
матричное уравнение:
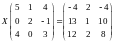
Найти собственные значения и собственные векторы матрицы:
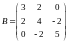
Показать, что векторы образуют базис и найти координаты вектора в этом базисе.
а. Ортогонализовать и дополнить до ортонормированного базис
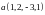 ,
,
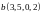 ,
,
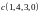 .
.
б. Найти матрицу линейного
преобразования (в базисе, в котором
заданы координаты всех векторов),
переводящего векторы
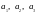 в векторы
в векторы
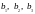 соответственно:
соответственно:
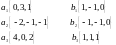
Найти угол между вектором
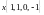 и подпространством, натянутым на векторы
и подпространством, натянутым на векторы
 и
и
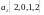 .
.
1. Найти ортогональное преобразование, приводящее квадратичную форму
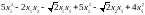 к каноническому виду. Выписать
канонический вид формы.
к каноническому виду. Выписать
канонический вид формы.
2. Определить вид, размеры и расположение поверхностей заданных уравнениями:
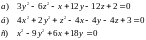
Вариант IV
а. Исследовать и решить систему уравнений:
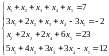
б. Найти
фундаментальную систему решений:
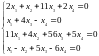
с. Решить
матричное уравнение:
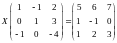
Найти собственные значения и собственные векторы матрицы:
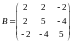
Показать, что векторы образуют базис и найти координаты вектора в этом базисе.
а. Ортогонализовать и дополнить до ортогонального базис
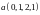 ,
,
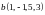 ,
,
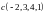 .
.
б. Найти матрицу линейного преобразования (в базисе, в котором заданы координаты всех векторов), переводящего векторы в векторы соответственно:
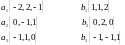
Найти угол между вектором и подпространством, натянутым на векторы
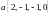 и
и
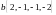 .
.
1. Найти ортогональное преобразование, приводящее квадратичную форму
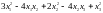 к каноническому виду. Выписать
канонический вид формы.
к каноническому виду. Выписать
канонический вид формы.
2. Определить вид, размеры и расположение поверхностей заданных уравнениями: