22.) Окружность (определение, каноническое ур-ние, ур-ние со смещённым центром, общее).

1.) Окружность - это геометрическое место точек плоскости, равноудалённых от одной и той же точки, называемой центром.

2.) x^2 + y^2 = R^2 - каноническое ур-ние.

3.)

4.) Ax^2 + Ay^2 +D*x + E*y + F = 0 – общее ур-ние окружности.

23.) * Эллипс (определение, каноническое уравнение, характеристики).

23.1.) Эллипс – геометрическое место точек плоскости, сумма расстояний от каждой из которых до двух данных точек F1 и F2, называемых фокусами, есть величина постоянная и равная 2а.

23.2.) Составим ур-ние эллипса:

Введём систему координат XOY так, чтобы фокусы располагались на оси OX и начало координат находилось посередине между ними.

Т.к. фокусы даны => дано расстояние между ними.

Обозначим |F2F1| = 2c , тогда точка F1 (c ; 0 ); F2 (-c ; 0 ).

Возьмём произвольную точку M ( x ; y) принадлежащую эллипсу.

Согласно определению MF1 + MF2 = 2a.

Используя формулу расстояния между двумя точками, получим расстояние: 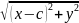+ 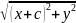= 2a.

Преобразуем полученное ур-ние:

= 2a - | ↑2

x^2 - 2xc + c^2 + y^2 = 4a^2 - 4a + x^2 + 2xc + c^2 + y^2 - Находим подобные и вычёркиваем, остаётся:

4a = 4a^2 + 4xc | : 4

a = a^2 + xc | ↑2

a^2 ( x^2 + 2xc + c^2 + y^2 ) = a^4 + 2a^2 xc + x^2 c^2

a^2 x^2 +2a^2 xc +a^2 c^2 + a^2 y^2 = a^4 + 2a^2 xc + x^2 c^2 - Находим подобные и вычёркиваем, остаётся:

x^2 (a^2 – c^2) + a^2 y^2 = a^2 (a^2 – c^2)

По определению эллипса, величина 2а > 2c.

2a > 2c => a > c => a^2 > c^2

a^2 – c^2 > 0.

Обозначим разность:

a^2 – c^2 = b^2

тогда последнее равенство примет вид:

x^2 * b^2 + y^2 * a^2 = a^2 * b^2 | : a^2 * b^2

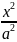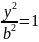+ Конаническое уравнение эллипса.

23.3.)

Характеристики:

a - большая полуось => 2a – большая ось

b - малая полуось => 2b - малая ось

с - полуфокусное расстояние.

При a > b:

Формула связи: b^2 = a^2 – c^2 ;

Фокусы: F1,2 = c ; 0);

Эсцентриситет: Ɛ = 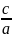< 1 ;

Эксцентриситет эллипса – это отношение его полуфокусного расстояния к длине большой оси:

Ɛ = . 0 < Ɛ < 1

Директриса - это прямые, перпендикулярные фокальной оси эллипса и отстоящие от его центра на расстояние :

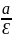x = - правая ; x = - левая.