17.) Выражение смешанного произведения через координаты сомножителей.

Пусть векторы a , b , c заданы в координатном пространстве:

a = (ax , ay , az) ; b = (bx , by , bz) ; c = (cx , cy , cz).

1.) Найдём их смешанное произведение.

Используя условный определитель, получим координаты векторного произведения первых двух векторов:

a x b = = - +

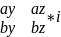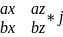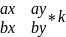
2.) Найдём, как сумму произведений одноимённых координат, скалярное произведение векторов (a x b) и с :

(a x b) * c =

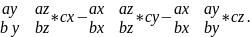
Здесь правая часть есть разложение определителя

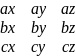по элементам третьего строки, поэтому

a x b * c = .

Cмешанное произведение трёх ненулевых векторов, равно определителю третьего порядка, составленного из координат перемножаемых векторов.

18.) Геометрический смысл смешанного произведения.

Пусть даны три некомпланарных вектора a , b , c , они могут составлять правую или левую тройки векторов.

Найдём их смешанное произведение:

1.) Перемножим векторы a и b векторно, получим новый вектор d, длина которого численно равна, площади параллелограмма, построенного на векторах a и b:

|d| = |a x b| = S.

2.) Умножим вектор d скалярно на вектор с :

d * c = |d| * NPd (c) = S * NPd (c)

т.к. проекция вектора с на направлениe d это h , где h = высота параллелепипеда, построенного на a , b ,c.

т.е. (a x b) * c = Sпар. (- + h).

(a x b) * c = - + V , где V – объём параллелепипеда.

|(a x b) * c| = V.

19.) Применение смешанного произведения.

1’) Установление компланарности векторов:

(a , b , c) = 0

.

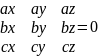2’) Нахождение объёмов параллелепипеда и пирамиды:

Vпарал. = |(a , b , c)|

Vпирам. = 1/6 * |(a , b , c)|.

3’) Определение взаимной ориентации векторов a , b , c – правая, если ( a , b , c) > 0;

a , b , c – левая, если (a , b , c) < 0.

20.) * Различные виды уравнения прямой на плоскости ( общее, с угловым коэффициентом, через заданную точку в данном направлении * через две точки * , в отрезках).

1. Общее уравнение прямой.

Ax + By + C = 0 - общее уравнение прямой , где A^2 + B ^2 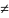0.

Исследование общего ур-ния:

- Пусть С = 0 , тогда Ax + By = 0 определит прямую, проходящую через начало координат, поскольку координаты начала (0,0) удовлетворяют этому уравнению.

- Пусть B = 0, тогда Ax + C = 0 и X = 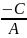. Обозначив 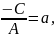получим x = a. Но уравнение x = a задаёт прямую, параллельную оси ОY, следовательно, Ах + C = 0 - уравнение прямой, параллельной оси OY.

- Пусть А = 0, тогда By + C = 0 и y = 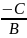. Обозначив 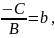получим, y = b. Таким образом, By + C = 0 – уравнение прямой, параллельной оси OX.

- Пусть C = 0 и B = 0, тогда прямая должна проходить через начало координат (C = 0) и одновременно быть параллельной оси Y (B=0), поэтому уравнение Ax = 0 или x = 0 – уравнение оси OY.

- Пусть C = 0 и A = 0, тогда By = 0 или y = 0 –уравнение оси OX.

2.

21.) Задачи на прямую (угол между прямыми, условие параллельности и перпендикулярности , расстояние от точки до прямой).