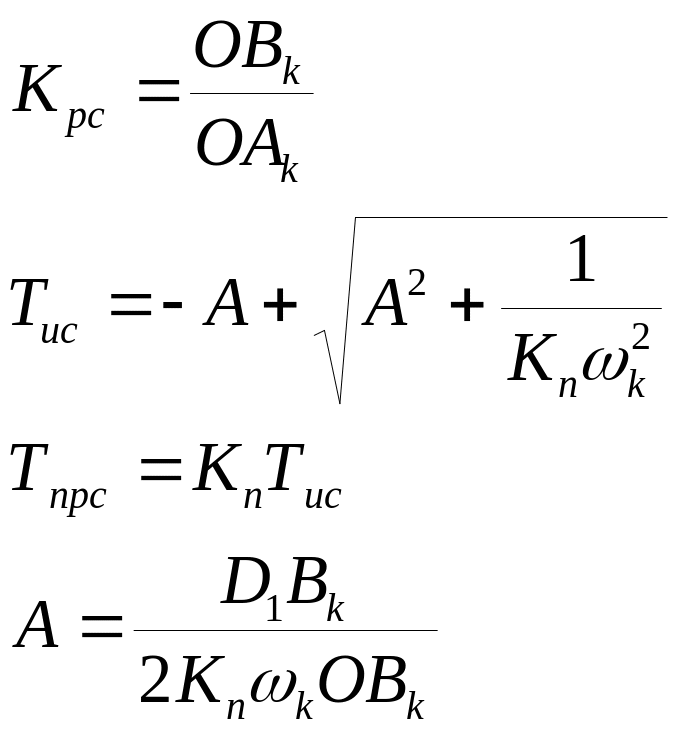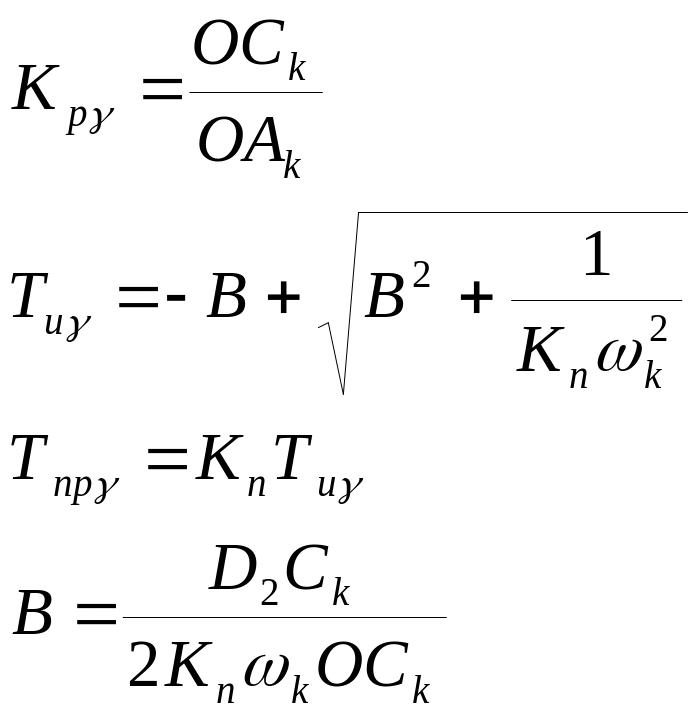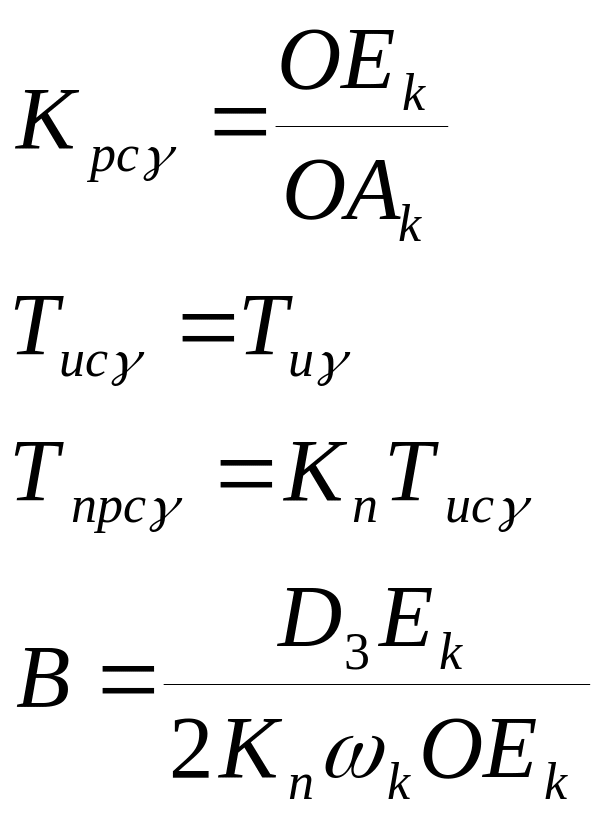- •Содержание
- •Часть 1 Линейные непрерывные аср
- •Устойчивость аср…………………………………………………………………… 66
- •Введение……………………………………………………………………………. 99
- •14.1. Введение……………………………………………………………………………. 104
- •Часть 2
- •Введение. Основные понятия и определения
- •Часть 1 линейные непрерывные аср
- •1. Основные сведения из динамики аср
- •1.1. Переходный процесс в аср
- •1.2 Устойчивость аср
- •1.3. Принцип суперпозиции. Типовые возмущения.
- •2. Применение преобразований лапласа в тау
- •2.2. Основные теоремы преобразования Лапласа
- •2.3. Передаточная функция
- •2.4. Переходный процесс в аср
- •3. Динамические характеристики аср
- •3.1. Комплексная частотная функция
- •4.3. Идеальное дифференцирующее звено
- •4.4. Идеальное интегрирующее звено
- •4.5. Апериодическое звено первого порядка
- •4.6. Реальное дифференцирующее звено
- •4.7. Инерционные звенья второго порядка
- •Типовые соединения звеньев
- •4.10.1. Введение
- •5. Основные свойства типовых объектов регулирования
- •6.1. Закон регулирования
- •10. Устойчивость аср
- •12.2.1. Введение
- •13.1 Введение
- •Регуляторами
- •14.1 Введение
- •Часть 2 Дискретные системы с цифровыми регуляторами
- •Список литературы
10. Устойчивость аср
10.1. Переходный процесс в АСР. Устойчивые и неустойчивые АСР
Общее уравнение динамики линейной АСР записывается в виде
![]()
где
- регулируемая величина;
- возмущающее воздействие.
Общее решение этого уравнения имеет вид:
![]() ,
,
где
-
![]() ый
корень характеристического уравнения
,
ый
корень характеристического уравнения
,
![]() -
ая
постоянная интегрирования.
-
ая
постоянная интегрирования.
Из этого решения очевидно, что ая составляющая переходного процесса будет стремиться к установившемуся значению в том случае, когда действительная часть соответствующего корня отрицательна. Если действительная часть корня положительна, то соответствующая составляющая переходного процесса будет уходить от установившегося значения и весь процесс будет расходящимся.
АСР, переходные процессы в которых затухают с течением времени, называют устойчивыми. АСР с расходящимися переходными процессами относят к неустойчивым.
Все реальные работоспособные системы должны быть устойчивыми.
Необходимое условие устойчивости
Для суждения об устойчивости системы нужно знать знаки действительной части корней характеристического уравнения системы, а для этого нужно решать эти уравнения. В радикалах решаются уравнения первой – четвертой степеней, уравнения пятой и выше степеней решаются только в численном виде по числовым коэффициентам уравнения.В связи с этим появляется необходимость уметь косвенным образом оценивать знаки корней характеристического уравнения.
Можно показать, что необходимым условием отрицательности корней характеристического уравнения системы, т.е. ее устойчивости, является положительность всех коэффициентов уравнения. Для АСР первого и второго порядков это необходимое условие является и достаточным.
Необходимое и достаточное условия устойчивости для АСР третьего и выше порядков определяются критериями устойчивости.
10.3. Критерии устойчивости
Алгебраический критерий устойчивости Гурвица
Для устойчивости замкнутой системы n-го порядка необходимо и достаточно, чтобы были положительными все n определителей, составленных из коэффициентов характеристического уравнения системы, причем определители берутся как главные миноры квадратной матрицы. Квадратная матрица записывается:
в первую строку выписываются коэффициенты уравнения через один, начиная со второго по старшинству;
во вторую строку выписываются коэффициенты уравнения через один, начиная
с первого по старшинству;
в третью и четвертую строки выписываются первая и вторая строки со сдвигом
на один элемент вправо.
На освободившиеся места в строках проставляются нули. Каждая последующая пара строк получается сдвигом на один элемент вправо двух предыдущих. Всего должно быть записано n строк и n столбцов, где n - порядок характеристического уравнения.
Например,
![]()
Квадратная матрица:
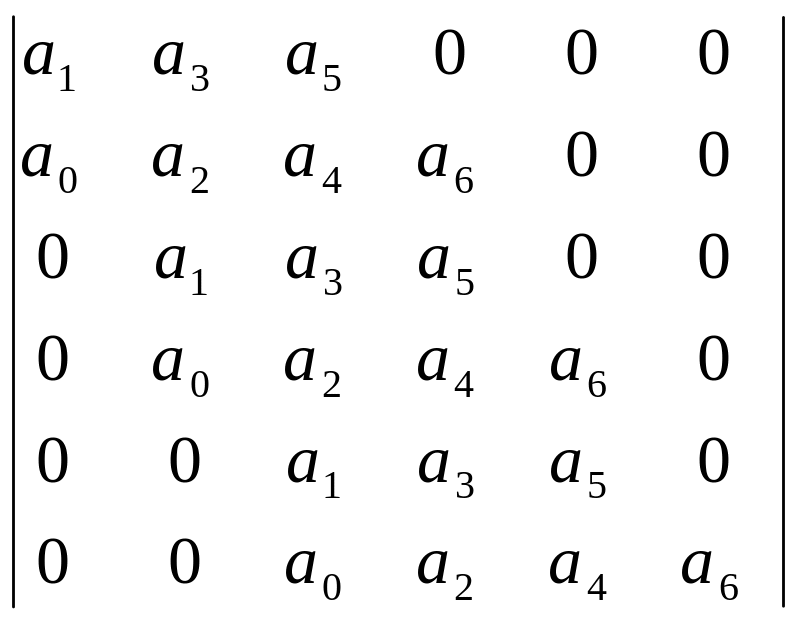
Условие устойчивости:
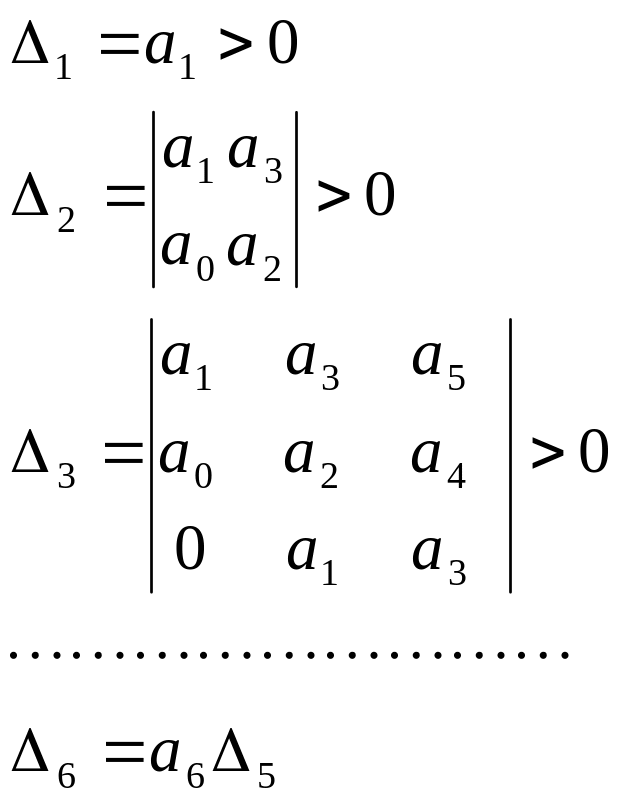
Так как все
коэффициенты должны быть положительными
и
![]() ,
то условие устойчивости записывается
в виде:
,
то условие устойчивости записывается
в виде:
![]()
![]()
![]()
![]()
Если свободный
член равен нулю
![]() , то в уравнении имеется нулевой корень.
, то в уравнении имеется нулевой корень.
Если предпоследний
определитель равен нулю
![]() ,
то в уравнении имеется чисто мнимый
корень.
,
то в уравнении имеется чисто мнимый
корень.
Следовательно, условиями границы устойчивости системы будут
![]() и
и
![]() .
.
10.3.2. Частотный критерий устойчивости Найквиста для статических систем
1. Если разомкнутая система устойчива, т.е. если передаточная функция разомкнутой системы не имеет полюсов в правой полуплоскости, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФХ разомкнутой системы при движении вдоль нее по часовой стрелке не охватывала точку (-1;j0) и не проходила через нее, например рисунок 10.1.
jV(ω)







 -1
ω=∞
-1
ω=∞







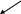 ω=0
u(ω)
ω=0
u(ω)




Рис.10.1.
2. Если разомкнутая
система неустойчива, т.е. если передаточная
функция разомкнутой системы имеет m
полюсов в правой полуплоскости, то для
устойчивости замкнутой системы необходимо
и достаточно, чтобы АФХ разомкнутой
системы при движении вдоль нее против
часовой стрелки охватывала точку (-1;j0)
![]() раз, например рисунок 10.2.
раз, например рисунок 10.2.
jV(ω)
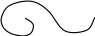




 m=2
ω=0
m=2
ω=0




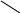
 -1
-1







 u(ω)
u(ω)
ω=∞
Рис.10.2.
10.3.3 Частотный
критерий Найквиста для астатических
систем
![]() -го
порядка астатизма
-го
порядка астатизма
В астатических АСР передаточная функция разомкнутой системы имеет полюсов в начале координат, т.е.
![]()
В этом случае характеристика
![]()
уходит в бесконечность при подходе к нулевой частоте как со стороны положительных, так и со стороны отрицательных значений , например рисунок 10.3.

jV(ω)

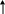 0
0

 ω
+∞
ω
+∞
 Wpc(jω)
Wpc(jω)
 0
u(ω)
0
u(ω)
 ω
-∞
ω
-∞
0
Рис.10.3.
Наличие двух
уходящих в бесконечность ветвей годографа
![]() при
при
![]() и
и
![]() делает АФХ незамкнутой и вносит в связи
с этим неопределенность в области
нулевой частоты.
делает АФХ незамкнутой и вносит в связи
с этим неопределенность в области
нулевой частоты.
Для возможности
применения критерия Найквиста и в этом
случае нужно кривую
замкнуть, устранив тем самым неопределенность
при
![]()
Для этого следует обойти нулевые корни характеристического уравнения, (нулевые полюсы передаточной функции), деформируя мнимую ось плоскости корней полуокружностью малого радиуса ρ (рис.10.4 а,б).






ρ ρ
б)
Рис.10.4.
Если обход осуществлять справа (против часовой стрелки), то нулевой корень следует отнести к левой полуплоскости. Если обход осуществлять слева (по часовой стрелке),
то нулевой корень относится к правой полуплоскости.
Если нулевой полюс
обходить полуокружностью радиуса
![]() (рис. 10.4), то годограф АФХ разомкнутой
системы дополняется полуокружностью
бесконечно большого радиуса R и кривая
АФХ замыкается.
(рис. 10.4), то годограф АФХ разомкнутой
системы дополняется полуокружностью
бесконечно большого радиуса R и кривая
АФХ замыкается.
Обходу нулевого полюса против часовой стрелки соответствует дополнение АФХ разомкнутой системы полуокружностью бесконечно большого радиуса R также против часовой стрелки.
Обходу нулевого полюса по часовой стрелке соответствует дополнение АФХ разомкнутой системы полуокружностью бесконечно большого радиуса R по часовой стрелке.
Если ограничиться
только рассмотрением положительного
диапазона частот (0![]() ),
не учитывая зеркального отображения
для отрицательных частот, то каждому
нулевому полюсу
),
не учитывая зеркального отображения
для отрицательных частот, то каждому
нулевому полюсу
![]() при обходе его четвертью окружности
радиусом
будет соответствовать дополнение
четвертью окружности радиуса
при обходе его четвертью окружности
радиусом
будет соответствовать дополнение
четвертью окружности радиуса
![]() ,
т.е. дугой
,
т.е. дугой
![]() бесконечно большого радиуса.
бесконечно большого радиуса.
Исходя из вышеизложенного, можно сформулировать следующие критерии устойчивости Найквиста для астатических систем:
1. Если передаточная
функция разомкнутой системы имеет
полюсов на мнимой оси или в начале
координат и не имеет полюсов в правой
полуплоскости, то для устойчивости
замкнутой системы необходимо и достаточно,
чтобы АФХ разомкнутой системы с ее
дополнением дугой
![]() бесконечно большого радиуса против
часовой стрелки не охватывала точку
(-1;j0) при движении вдоль нее по часовой
стрелке.
бесконечно большого радиуса против
часовой стрелки не охватывала точку
(-1;j0) при движении вдоль нее по часовой
стрелке.
2. Если передаточная
функция разомкнутой системы имеет
полюсов на мнимой оси или в начале
координат и m полюсов в правой полуплоскости,
то для устойчивости замкнутой системы
необходимо и достаточно, чтобы АФХ
разомкнутой системы с ее дополнением
дугой
бесконечно большого радиуса по часовой
стрелке охватывала точку (-1;j0)
![]() раз при движении вдоль нее против часовой
стрелки.
раз при движении вдоль нее против часовой
стрелки.
10.4. Влияние параметров АСР на ее устойчивость
Критерии устойчивости позволяют при известных параметрах АСР делать заключение о ее устойчивости. С их помощью можно также проследить влияние отдельных параметров на устойчивость, оценить степень устойчивости и тем самым оценить интенсивность затухания переходных процессов в АСР.
Существенное влияние на качество АСР оказывает ее коэффициент передачи. В статических АСР коэффициент передачи определяет величину статической ошибки. Чем больше коэффициент передачи, тем меньше статическая ошибка.
Следовательно, с точки зрения статической точности регулирования нужно увеличивать коэффициент передачи.
Однако, по мере
роста его при прочих равных условиях
ухудшается устойчивость системы. Если
АФХ разомкнутой системы при единичном
коэффициенте передачи (рис. 10.5)
![]() ,
то при
,
то при
![]() АФХ разомкнутой системы
АФХ разомкнутой системы
![]() .
.
jV(ω)
Akp(ωkp)


 -1
ω=∞
ω=0
-1
ω=∞
ω=0

ωkp 0 u(ω)
Wpc1(jω)
Рис.10.5.
По мере увеличения коэффициента передачи модули АФХ увеличиваются, АФХ разомкнутой системы располагается все ближе и ближе к критической точке (-1;j0).
При некотором значении коэффициента передачи АФХ разомкнутой системы пройдет через точку (-1;j0) и АСР выйдет на границу устойчивости. Значение коэффициента передачи разомкнутой АСР, при котором замкнутая система находится на границе устойчивости, при прочих равных условиях, называют критическим или предельным.
Из рисунка 10.5. имеем:
![]()
![]()
где ![]() значение
модуля АФХ разомкнутой системы при
критической частоте, причем под
критической частотой понимают частоту,
при которой АФХ разомкнутой системы
при единичном коэффициенте передачи
пересекает отрицательную вещественную
полуось.
значение
модуля АФХ разомкнутой системы при
критической частоте, причем под
критической частотой понимают частоту,
при которой АФХ разомкнутой системы
при единичном коэффициенте передачи
пересекает отрицательную вещественную
полуось.
АСР, состоящую из устойчивых звеньев, в замкнутом состоянии всегда можно сделать устойчивой надлежащим подбором параметров системы, например, ее коэффициента передачи.
При этом в достаточной мере могут быть удовлетворены и другие требования к качеству системы. Системы регулирования, которые можно сделать устойчивыми только подбором ее параметров без изменения структуры, называют структурно-устойчивыми системами.
АСР, которые не могут быть сделаны устойчивыми путем только изменения значений параметров системы, называют структурно-неустойчивыми. Для придания устойчивости структурно-неустойчивым АСР необходимо изменять их структуру путем введения корректирующих устройств. Корректирующие устройства могут быть последовательными, параллельными и в виде обратных связей. Последовательные и параллельные корректирующие устройства реализуют дифференцирующими звеньями.
В качестве корректирующих устройств в виде обратной связи применяют жесткие и упругие обратные связи.
1. Идеальная жесткая обратная связь
![]()
![]()
Жесткая обратная связь с инерционностью первого порядка
![]()
![]()
![]()
3. Жесткая обратная связь с инерционностью второго порядка
![]()
![]()
4. Упругая обратная связь с инерционностью первого порядка
![]()
![]()
![]()
где Ти - постоянная времени звена обратной связи, называемая временем изодрома.
11. ОЦЕНКА КАЧЕСТВА АСР
11.1. Прямые показатели качества переходных процессов в замкнутой АСР
Работоспособность любой замкнутой АСР определяется ее устойчивостью, что в свою очередь предопределяется структурой системы.
Переходные же
процессы зависят не только от структуры
системы и ее параметров, но и от характера
воздействий, приложенных к ней. В связи
с этим для оценки качества регулирования
и динамических свойств АСР вводят
типовые воздействия, к которым относят
единичные скачкообразную
![]() и импульсную
и импульсную
![]() функции; воздействие, изменяющееся с
постоянной скоростью или постоянным
ускорением; гармоническое воздействие.
функции; воздействие, изменяющееся с
постоянной скоростью или постоянным
ускорением; гармоническое воздействие.
Из приведенных типовых воздействий чаще применяют единичную скачкообразную функции . При этом используют прямые показатели качества
(рис. 11.1):

 y y
y y

 y1
y3
∆H
y1
y3
∆H





 y1
y3
∆H
y1
y3
∆H


 y2
y2
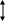
 yyct=y(∞)
∆H 0
t
yyct=y(∞)
∆H 0
t


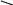


 y2
y2
0 t
 tp
tp
tp
tp

а) статическая АСР б) астатическая АСР
Рис.11.1.
максимальное отклонение
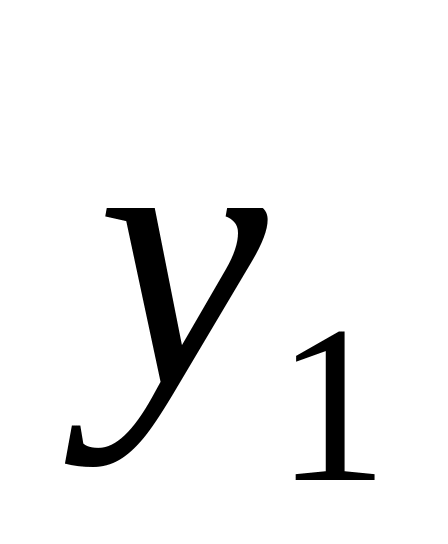 регулируемой величины (динамическая
ошибка
регулируемой величины (динамическая
ошибка
регулирования) (рис. 11.1. а,б)
статическая ошибка
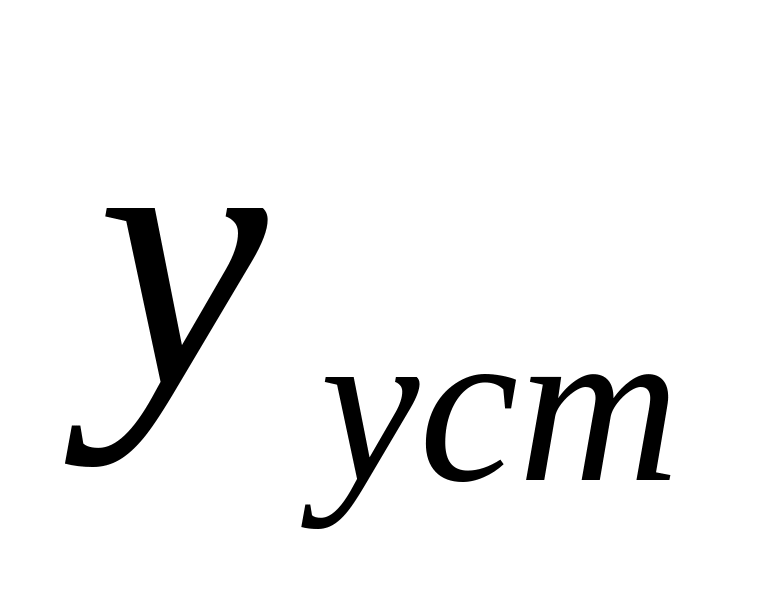 в установившемся режиме для статических
АСР
в установившемся режиме для статических
АСР
(рис. 11.1 а)
- перерегулирование
![]()
для статических (рис.11.1 а)
и
![]()
для астатических АСР (рис.11.1 б).
-
зона нечувствительности
![]() (рис.11.1 а,б)
(рис.11.1 а,б)
-
время регулирования
![]() (рис.11.1 а,б)
(рис.11.1 а,б)
- степень затухания
![]()
для колебательных процессов (рис.11.1 а,б)
Степенью затухания называют отношение разности двух соседних одинаково направленных амплитуд колебаний к первой из них.
Следовательно, качество процессов регулирования можно оценить путем решения дифференциального уравнения системы и построения графика переходного процесса.
Однако, решение в аналитическом виде возможно только в случае линейных дифференциальных уравнений с постоянными коэффициентами и сопряжено с трудностями определения корней характеристического уравнения.
Вследствие этого широко применяют косвенные оценки качества АСР, к числу которых относят корневые, интегральные и частотные показатели.
Корневые показатели качества АСР
Корневые показатели определяются расположением корней характеристического уравнения замкнутой системы в комплексной плоскости, при этом ориентируются на корень, наиболее близкий к мнимой оси.
В соответствии с этим различают: степень апериодической и степень колебательной устойчивости. Степенью апериодической устойчивости называют абсолютную величину действительного корня, расположенного наиболее близко к мнимой оси (, рис. 11.2 а). Степенью колебательной устойчивости называют отношение вещественной части наиболее близкого к мнимой оси комплексного корня к коэффициенту при его мнимой части (m, рис. 11.2 б),
jω jω




![]() ω
ω
![]()

η 0 α α 0 α

а) б)
Рис.11.2.
т.е. тангенс угла (), образованного верхней мнимой полуосью комплексной плоскости и прямой, проведенной из начала координат через ближайший к мнимой оси комплексный корень. Степень колебательной устойчивости однозначно определяет величину степени затухания:
![]()
11.3. Интегральные критерии качества АСР
Простейшей линейной интегральной оценкой для апериодических процессов является интеграл
![]()
где
![]() -
значение регулируемой величины
(отклонение ее от номинального значения,
принимаемого равным нулю) для астатических
АСР
-
значение регулируемой величины
(отклонение ее от номинального значения,
принимаемого равным нулю) для астатических
АСР
(рис. 11.3 а)
и
![]() -
отклонение текущего значения регулируемой
величины от ее
-
отклонение текущего значения регулируемой
величины от ее
нового установившегося значения для статических систем
(рис. 11.3 б)
 y
y
y
y
∆y ∆y S







 S
S


 ∆y(t)
∆y(t)


 yустyст
yустyст
y(t),∆y(t) y(t)

0 t 0 t
а) астатическая АСР б) статическая АСР
Рис.11.3.
В
устойчивой системе
![]() при
(рис. 11.3 а,б) и этот интеграл будет конечен.
Линейная интегральная оценка является
неприемлемой для оценки колебательных
процессов, так как в этих случаях может
оказаться, что интегральная оценка
будет минимальной при больших
знакопеременных отклонениях регулируемой
величины (рис. 11.4 а,б). В связи с этим для
оценки качества колебательных процессов
применяют квадратичный интегральный
критерий
при
(рис. 11.3 а,б) и этот интеграл будет конечен.
Линейная интегральная оценка является
неприемлемой для оценки колебательных
процессов, так как в этих случаях может
оказаться, что интегральная оценка
будет минимальной при больших
знакопеременных отклонениях регулируемой
величины (рис. 11.4 а,б). В связи с этим для
оценки качества колебательных процессов
применяют квадратичный интегральный
критерий
![]() ,
,
где ![]() - отклонение текущего значения регулируемой
величины от ее нового установившегося
значения в конце процесса регулирования
(рис. 11.4 а,б) – динамическая ошибка. (Для
астатических АСР
- отклонение текущего значения регулируемой
величины от ее нового установившегося
значения в конце процесса регулирования
(рис. 11.4 а,б) – динамическая ошибка. (Для
астатических АСР
![]() ).
).
 y
y
y
y
 ∆y ∆y
∆y ∆y
S S








 ∆y(t)
∆y(t)
 y(t)
∆y(t)
yуст=y(∞)
y(t)
∆y(t)
yуст=y(∞)
 y(t)
y(t)
0 t 0 t
а) астатическая АСР б) статическая АСР
Рис.11.4.
Квадратичный интегральный критерий не зависит от знаков отклонения регулируемой величины и тем самым однозначно определяет как величины отклонений, так и длительность процесса регулирования.
Для обеспечения надлежащего качества переходных процессов, т.е. качества АСР, необходимо стремиться к минимизации интегральных оценок.
Их вычисление можно осуществить различными математическими приемами. Так, линейная интегральная оценка легко определяется с помощью преобразований Лапласа, квадратичная - с помощью формулы Релея - Парсеваля на основе частотных спектров входной и выходной функций.
При использовании ЭВМ удобно применить один из численных методов интегрирования функций.
11.4. Типовые процессы регулирования
11.4.1. Апериодический процесс с минимальным временем регулирования
Показателями
качества (рис. 11.5 ) являются отклонения
![]() регулируемой величины (динамическая
ошибка для астатической АСР и статическая
ошибка для статической АСР) и время
регулирования
регулируемой величины (динамическая
ошибка для астатической АСР и статическая
ошибка для статической АСР) и время
регулирования
![]() .
.

 y
y
y
y





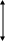

y1(t)=y1 y1(t)=y1(=yуст=y(∞))

0 t 0 t
 tp
tp
tp
tp

а) астатическая АСР б) статическая АСР
Рис.11.5.
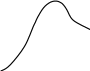
11.4.2. Процесс регулирования с 20%-ым перерегулированием
1. Статическая АСР
За время
регулирования
![]() отклонение регулируемой величины
достигает установившегося значения, а
затем превышает его на 20% (рис. 11.6 а)
отклонение регулируемой величины
достигает установившегося значения, а
затем превышает его на 20% (рис. 11.6 а)

 y
y
y
y
0.2y1
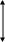


y1(t)=yуст=y(∞) y1(t)=у1
 t
t
t
t
 0
0
0.2y1
0
0
0.2y1
 tp
МИН
tрМИН
tp
МИН
tрМИН

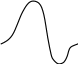
а) статическая АСР б) астатическая АСР
Рис.11.6.
2. Астатическая АСР
За время регулирования отклонение регулируемой величины достигает прежнего (нулевого) значения, а затем достигает отрицательного максимума и опять возвращается к исходному значению. Вторая амплитуда отклонения составляет 20% динамической ошибки (рис. 11.6 б).
11.4.3. Процесс регулирования с минимальным квадратичным интегральным критерием
Процесс характеризуется наибольшими перерегулированием (40÷45)%, временем регулирования, регулирующим воздействием, но наименьшими величинами амплитуд колебаний регулируемой величины (рис.11.7).
 y
y



![]()












 y1
y1








 y3
y5
y3
y5





 0
y2
y4
t
0
y2
y4
t
tр

Рис.11.7.
11.5. Частотные критерии качества АСР
11.5.1. Запас устойчивости по модулю и фазе
Запасом
устойчивости по модулю (с) называют
длину отрезка, равную расстоянию от
точки пересечения АФХ разомкнутой
системы с отрицательной вещественной
полуосью комплексной плоскости до точки
с координатами (-1;![]() )
(рис.11.8).
)
(рис.11.8).
 jV(ω)
jV(ω)

c

 -1
-1


 0
ω=∞ u(ω)
0
ω=∞ u(ω)
 Wpc(jω)
ω
Wpc(jω)
ω
0
Рис.11.8.
Запасом устойчивости по фазе () называют угол, образованный отрицательной вещественной полуосью комплексной плоскости и вектором АФХ разомкнутой системы,
модуль которого равен единице.
11.5.2. Частотный показатель колебательности
Степень удаления АФХ разомкнутой системы от критической точки (-1; ) может быть оценена также величиной максимума АЧХ замкнутой системы.
Допустим, что АФХ разомкнутой системы имеет вид, показанный на рисунке 11.9.
 jV(ω)
jV(ω)
-1


 B
ωi
0
ω=∞ u(ω)
B
ωi
0
ω=∞ u(ω)
Аi ω
Wpc(jω) 0
Рис.11.9.
АЧХ
замкнутой системы определяется через
![]() как:
как:
![]()
В
соответствии с рисунком 11.9 для
![]() -ой
частоты можно записать:
-ой
частоты можно записать:
![]() ,
,
![]() ,
,
Если в
АСР имеется интегрирующее звено, то
модуль АФХРС уходит в бесконечность
при
![]() ,
например, рисунок 11.9. В этом случае
отношение длин отрезков ОАi
и ВАi
при
равно
единице. Если система статическая, то
это отношение при
близко к единице
,
например, рисунок 11.9. В этом случае
отношение длин отрезков ОАi
и ВАi
при
равно
единице. Если система статическая, то
это отношение при
близко к единице

При
повышении частоты точка
![]() перемещается вверх по характеристике.
При этом, если АФХРС располагается
достаточно далеко от точки (-1;
),
то длина отрезка ВАi
будет
все время больше длины отрезка ОАi
и при
перемещается вверх по характеристике.
При этом, если АФХРС располагается
достаточно далеко от точки (-1;
),
то длина отрезка ВАi
будет
все время больше длины отрезка ОАi
и при
![]() стремится
к единице. Одновременно длина отрезка
ОАi,
уменьшаясь, стремится к нулю. Поэтому
при изменении частоты
стремится
к единице. Одновременно длина отрезка
ОАi,
уменьшаясь, стремится к нулю. Поэтому
при изменении частоты
![]() АЧХЗС монотонно убывает от единицы до
нуля
АЧХЗС монотонно убывает от единицы до
нуля
(рис. 11 10, кривая 1).
Если
АФХРС расположена близко к точке (-1;
),
то длина отрезка ВАi
при
некоторых значениях частот меньше длины
отрезка ОАi.
Поэтому в некотором диапазоне частот
![]() .
АЧХЗС возрастает от единицы до некоторого
максимума, затем (вследствие того, что
ОАi
.
АЧХЗС возрастает от единицы до некоторого
максимума, затем (вследствие того, что
ОАi![]() при
,
а ВАi
при
,
а ВАi![]() )
стремится к нулю (рис. 11.10, кривая 2 ).
)
стремится к нулю (рис. 11.10, кривая 2 ).
Чем
ближе АФХРС к точке (-1;
),
тем больше максимум АЧХЗС, и, если АФХРС
проходит через точку (-1;
),
то
![]() ,
т.е. в точке, соответствующей
,
т.е. в точке, соответствующей
![]() АЧХЗС терпит разрыв (рис. 11.10, кривая 3).
АЧХЗС терпит разрыв (рис. 11.10, кривая 3).


 A3
A3
 3
3


 2
2
1 1
 0
ω
0
ω
ωрез
Рис.11.10.
Таким образом, чем больше максимум АЧХЗС, тем ближе АФХРС к точке (-1; ), т.е. тем меньше запас устойчивости замкнутой АСР. Частоту, соответствующую максимуму АЧХЗС, называют резонансной .
Величину максимума АЧХЗС называют частотным показателем колебательности (М). Между показателем колебательности М, запасом устойчивости по модулю С и запасом устойчивости по фазе имеются однозначные зависимости:
![]()
![]() .
.
РАСЧЕТ НАСТРОЕК ЛИНЕЙНЫХ НЕПРЕРЫВНЫХ ОДНОКОНТУРНЫХ АСР
12.1 Определение оптимальных настроек линейных одноконтурных АСР
по АФХ объекта регулирования.
12.1.1. Условие оптимальности
Линейная АСР может рассматриваться как частотный фильтр, через который проходят входные воздействия прежде, чем попасть на ее выход .
Идеальной системой регулирования называют систему, которая обладает абсолютными фильтрующими свойствами, т.е. систему, АЧХ которой по каналу возмущающего воздействия равна нулю во всем диапазоне частот . С точки зрения наилучшего реагирования на управляющее воздействие АЧХ системы по каналу этого воздействия должна быть равна единице.
В соответствии с этим можно записать:
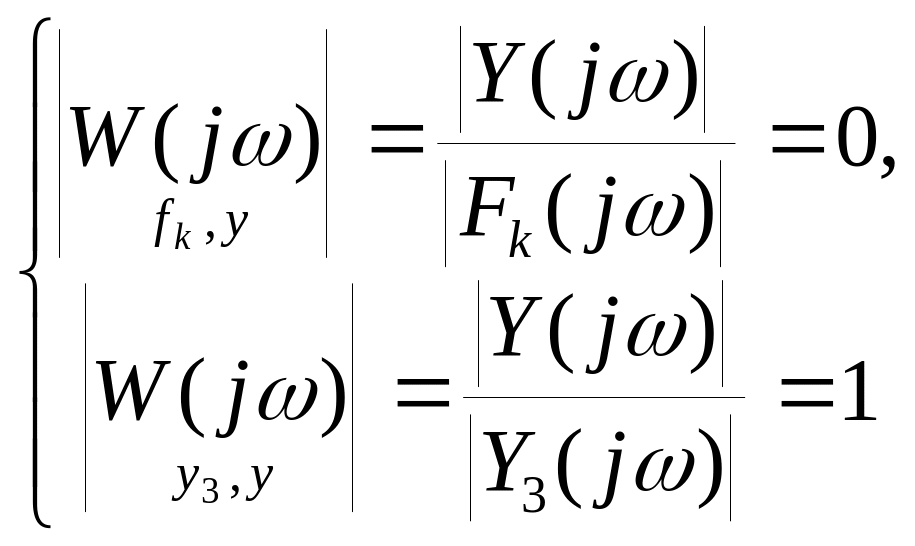
В реальных АСР эти условия выполнены быть не могут. Задача выбора параметров настройки и заключается в том, чтобы в наибольшей степени приблизить АЧХ системы к приведенным характеристикам. Эта задача является типичной задачей теории приближения функций. Так как в большинстве АСР возмущающие воздействия имеют наибольшую интенсивность в области низких частот, а реальные элементы, из которых состоят системы регулирования, обладают некоторой инерционностью, то в целом АСР являются низкочастотными фильтрами.
Поэтому в качестве приближения целесообразно выбрать такой метод, который гарантировал бы наилучшее приближение в окрестности точки с нулевой частотой. Поставленному требованию достаточно хорошо удовлетворяет метод приближения путем разложения функции в ряд Тейлора.
![]()
Отклонение частотной характеристики от нуля тем меньше, чем больше членов ряда обращаются в нули.
Отсюда, условия оптимальности запишутся в виде:


Исходя из этих условий, для различных законов регулирования получены условия оптимальности, приведенные в таблице 12.1.
Таблица12.1.
Закон Регулирования |
Параметры настройки |
Условие оптимальности |
П
И
ПИ
ПИД |
|
,
|
12.1.2. Графо - аналитический расчет настроек АСР по показателю колебательности
Условие обеспечения заданного значения показателя колебательности
В качестве меры устойчивости системы используют максимум амплитудно - частотной характеристики системы по каналу управляющего воздействия, т.е. показатель колебательности (М). Чем больше максимум АЧХЗС, тем ближе АФХРС к критической точке (-1; ) комплексной плоскости и, следовательно, тем меньше запас устойчивости имеет система.
Чтобы система имела некоторый заданный запас устойчивости, т.е. чтобы максимум АЧХЗС не превышал некоторого значения Мзад, необходимо, чтобы АФХРС не заходила во внутрь области, ограниченной окружностью радиуса
![]()
с центром на отрицательной вещественной полуоси на расстоянии
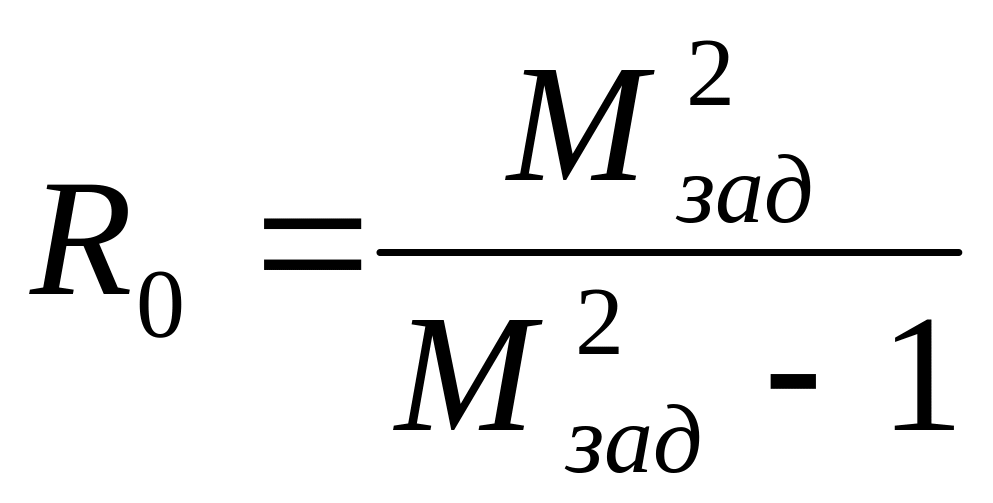
от начала координат (рис. 12.1 а)
 jV(ω)
jV(ω)
jV(ω)
jV(ω)
rзад rзад



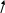

 Mзад
M<Mзад
Mзад
M=Mзад
Mзад
M<Mзад
Mзад
M=Mзад


0 u(ω) 0 u(ω)
R0 R0



Wpc(jω)
а) б)
Рис.12.1.
При равенстве показателя колебательности его заданному значению АФХРС должна касаться этой окружности (рис. 12.1.б).
Проведем прямую ОА, касающуюся окружности заданного индекса Мзад
(рис. 12.2).
Из рисунка 12.2 имеет:
![]()
Подставляя
сюда значения
![]() и
и
![]() ,
получим:
,
получим:
![]()
![]()
 jV(ω)
jV(ω)
R0
Mзад rз





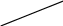 01
ß
0
u(ω)
01
ß
0
u(ω)
A
Рис.12.2.
Это означает, что
независимо от масштаба графика окружность
с индексом Мзад
всегда остается касательной к прямой
ОА, проведенной из начала координат под
углом
![]() к отрицательной вещественной полуоси.
Следовательно, при величине коэффициента
передачи регулятора, соответствующей
заданному запасу устойчивости системы,
окружность с индексом Мзад
должна касаться одновременно АФХРС
(рис. 12.1 б) и прямой, проведенной под
углом
к отрицательной вещественной полуоси
из начала координат комплексной плоскости
(рис. 12.2).
к отрицательной вещественной полуоси.
Следовательно, при величине коэффициента
передачи регулятора, соответствующей
заданному запасу устойчивости системы,
окружность с индексом Мзад
должна касаться одновременно АФХРС
(рис. 12.1 б) и прямой, проведенной под
углом
к отрицательной вещественной полуоси
из начала координат комплексной плоскости
(рис. 12.2).
Введя АФХРС при единичном коэффициенте передачи регулятора, несложными геометрическими построениями можно показать, что:
![]() ,
,
где
![]() -
радиус окружности, касающейся одновременно
АФХРС
и прямой, проведенной под углом
-
радиус окружности, касающейся одновременно
АФХРС
и прямой, проведенной под углом
к отрицательной вещественной полуоси из начала координат комплексной плоскости.
Отсюда вытекает следующий порядок расчета оптимальных настроек регуляторов.
12.1.2.2. АСР с П - регулятором
Вычерчивают АФХРС
 при Кр=1
(единичном коэффициенте передачи), т.е.
при Кр=1
(единичном коэффициенте передачи), т.е.
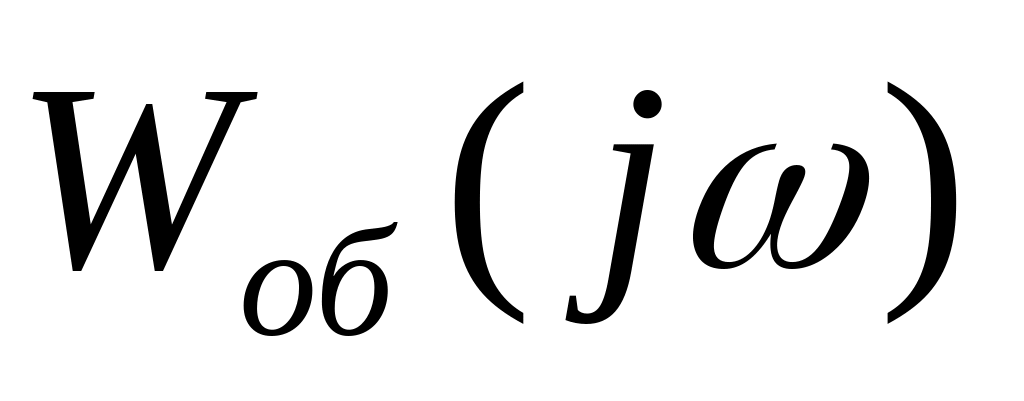 (рис.12.3)
(рис.12.3)
jV(ω)
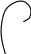

 Mзад
r
Mзад
r

01 ß 0 u(ω)
A
Wpc(jω)
Рис.12.3.
Из начала координат проводят прямую под углом
к отрицательной вещественной полуоси.
Чертят окружность с центром на вещественной отрицательной полуоси, касающуюся одновременно АФХ объекта регулирования и этой прямой.
По замеренному значению радиуса окружности находят значение оптимального коэффициента передачи
12.1.2.3. АСР с И - регулятором
1. Для удобства графических построений АФХ И - регулятора представляют в виде:
![]()
где
![]() - условный коэффициент
передачи И - регулятора;
- условный коэффициент
передачи И - регулятора;
![]() - условная постоянная
времени И - регулятора
- условная постоянная
времени И - регулятора
2. По АФХ объекта (статического) строят АФХРС при =1 и некотором значении постоянной , величину которой можно выбирать любой, удобной для построения характеристики.
![]()
Для построения этой характеристики нужно каждый вектор , предварительно разделенный по модулю на ,повернуть на 90º по часовой стрелке (рис. 12 4).
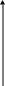 jV(ω)
jV(ω)




 Аоб(ωi)
0
φоб(ωi)
u(ω)
Аоб(ωi)
0
φоб(ωi)
u(ω)
Tpωi 900
 Aоб(ωi)
Aоб(ωi)
ωi
ωi
Рис.12.4.
Проводят прямую под углом
к отрицательной вещественной полуоси и чертят окружность с центром на этой полуоси, касающуюся одновременно этой прямой и характеристики . Величина , обеспечивающая необходимую величину Мзад, определяется как:
![]()
Следовательно,
![]()
![]()
12.1.2.4. АСР с ПИ - регулятором
Разомкнутая АСР с ПИ - регулятором описывается передаточной функцией
![]()
При Кр=1
![]()
Отсюда
![]()
Это означает, что
включение ПИ - регулятора приводит к
добавлению к векторам
этих же векторов, повернутых на 90º по
часовой стрелке и измененных по модулю
в
![]() раз (рис. 12.5.a.).
раз (рис. 12.5.a.).
 jV(ω)
jV(ω)
jV(ω)
jV(ω)
 kp=1
kp=1














![]() φоб(ωi)
r3
r2
φоб(ωi)
r3
r2





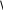 u(ω)
o3
o2
0
u(ω)
u(ω)
o3
o2
0
u(ω)

 0
φрс(ωi)
ß
0
φрс(ωi)
ß

 900
Aоб(ωi)
900
Aоб(ωi)
 Apc(ωi)
Tи=а
Apc(ωi)
Tи=а
∆A(ωi) Tи=с Tи=b
 α
α
 ωi
ωi
a) б)
Рис.12.5.
Отсюда следует, что АФХРС при Кр=1 может быть построена графически при наличии графика или рассчитана аналитически.
Из рисунка 12.5 а имеем:

откуда
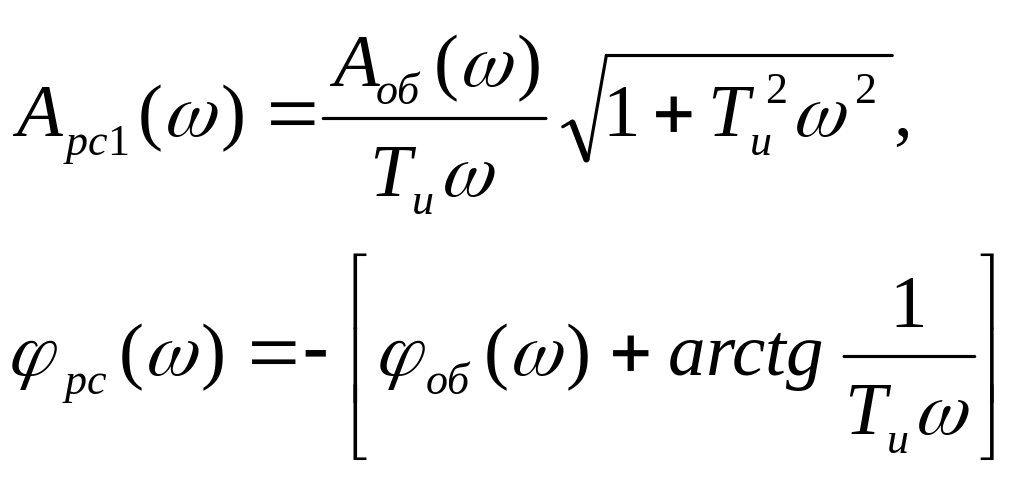
Здесь
![]() берется по абсолютному значению. Далее
расчет настроек производят в порядке:
берется по абсолютному значению. Далее
расчет настроек производят в порядке:
Тем или иным способом строят семейство АФХРС при Кр=1 и некотором
фиксированном значении времени изодрома Ти, (т.е. временем изодрома Ти
задаются).
Проводят прямую из начала координат под углом к отрицательной вещественной полуоси и строят окружности, касающиеся одновременно этой прямой и характеристик для различных значений Ти (рис.12.5 б).
Вычисляют оптимальные значения коэффициента передачи регулятора по
найденным значениям радиусов соответствующих окружностей
![]()
По результатам расчета в плоскости параметров Кр-Ти строят границу заданного
показателя колебательности (рис. 12.6)
 kp
kp





 М<Mзад
М=Mзад
М<Mзад
М=Mзад



 кр
опт
кр
опт

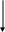




 М>Mзад
М>Mзад
0 Ти опт Tи
Рис.12.6.
Оптимальной
настройке будет соответствовать точка
в той области, для которой
![]() .
Этому условию удовлетворяет точка
касания касательной, проведенной из
начала координат к границе заданного
показателя колебательности (к границе
устойчивости, заданной показателем
колебательности М).
.
Этому условию удовлетворяет точка
касания касательной, проведенной из
начала координат к границе заданного
показателя колебательности (к границе
устойчивости, заданной показателем
колебательности М).
12.1.2.5 АСР с ПИД - регулятором
Для определения оптимальных настроек ПИД - регулятора строится семейство АФХРС для единичного коэффициента передачи регулятора и различных значений времени изодрома при фиксированном оптимальном значении отношения времени предварения ко времени изодрома
![]()
Передаточная функция разомкнутой системы с ПИД - регулятором имеет вид:
![]()
При Кр=1
![]() ,
,
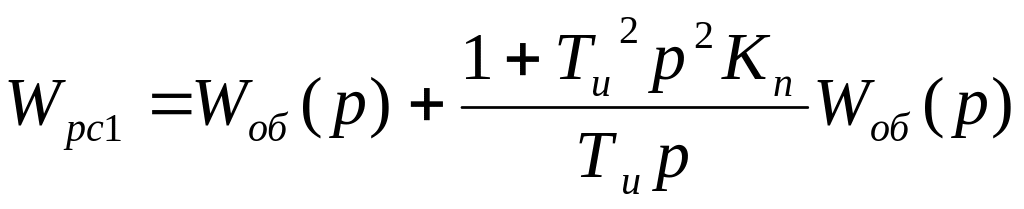 ,
,
![]()
Подставив
![]() ,
получим:
,
получим:
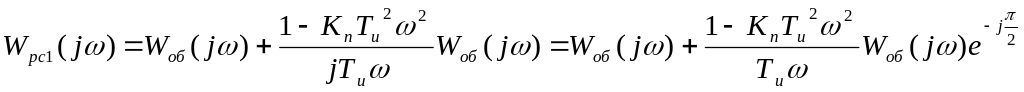
Следовательно,
включение ПИД - регулятора приводит к
добавлению к векторам
этих же
векторов, повернутых на 90º по часовой
стрелке и измененных по модулю в
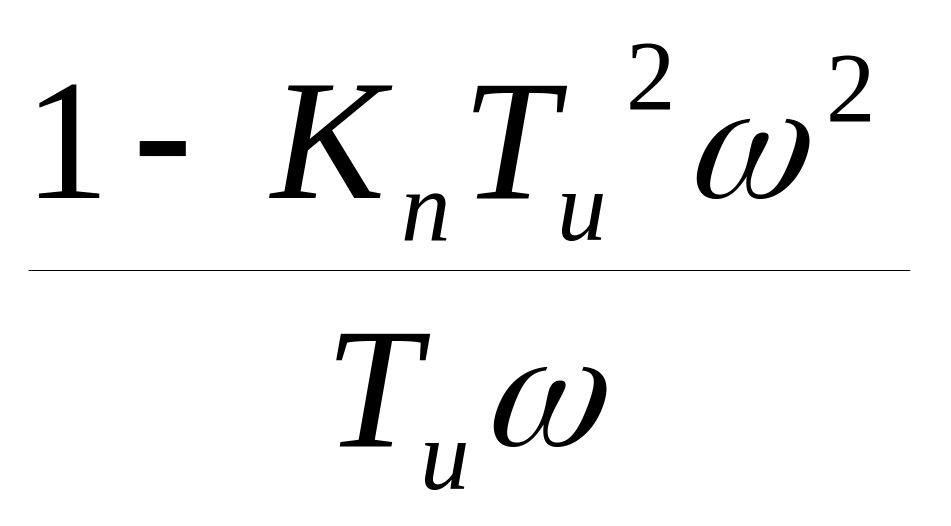 раз (рис. 12.7)
раз (рис. 12.7)
jV(ω)
φоб(ωi)
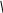 u(ω)
u(ω)
0 φрс(ωi)
 ωi
900
Aоб(ωi)
ωi
900
Aоб(ωi)
 Apc1(ωi)
Apc1(ωi)
 ωi
ωi

 α
α
ωi
![]()
Рис.12.7.
В соответствии с рисунком 12.7
![]() ,
,
![]() ,
,
![]() .
.
Подставив значение
![]() ,находим:
,находим:
![]()
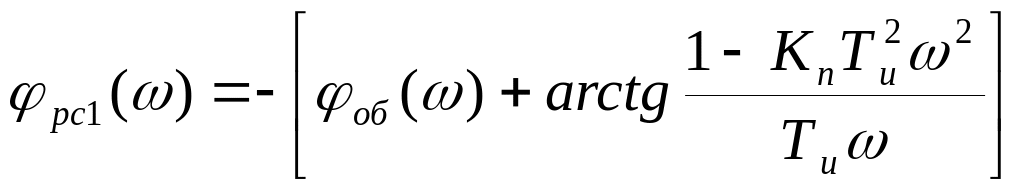
Далее расчет настроек ПИД регулятора аналогичен расчету настроек ПИ - регулятора.
12.1.2.6. Расчет приближенных настроек П и ПИ - регуляторов с помощью АФХОР
Из рассмотренной методики расчета оптимальных настроек АСР вытекает, что основное значение для расчета имеет участок АФХОР, расположенный вблизи ее пересечения с отрицательной вещественной полуосью комплексной плоскости.
Это обстоятельство позволяет осуществить приближенную настройку регулятора, предполагая, что в окрестности частоты, соответствующей точке пересечения характеристики с отрицательной вещественной полуосью, АФХОР мало отличается от характеристики интегрирующего звена с запаздыванием.
На этом основании для случая М=1,62 (что соответствует =0,75 ) получены упрощенные расчетные соотношения для П и ПИ - регуляторов, приведенные в таблице 12.2.
Таблица 12.2
-
Приближенная настройка
П – регулятора
ПИ – регулятора
Кропт
Кропт
Тиопт
Для астатических объектов
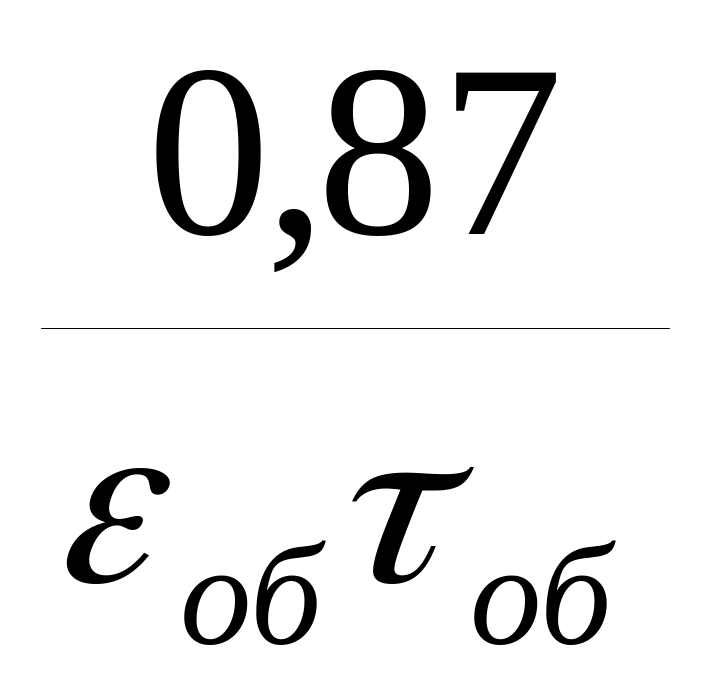

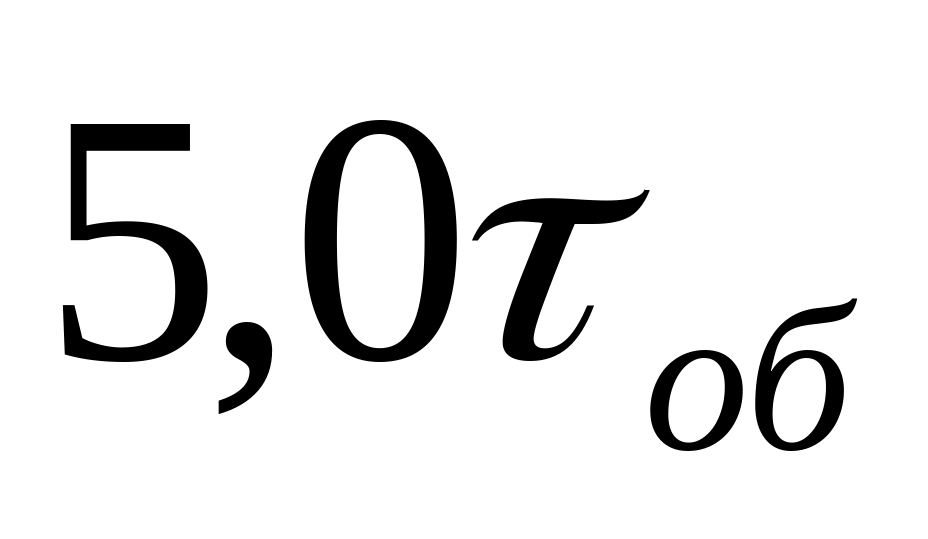
Для астатических и статических объектов
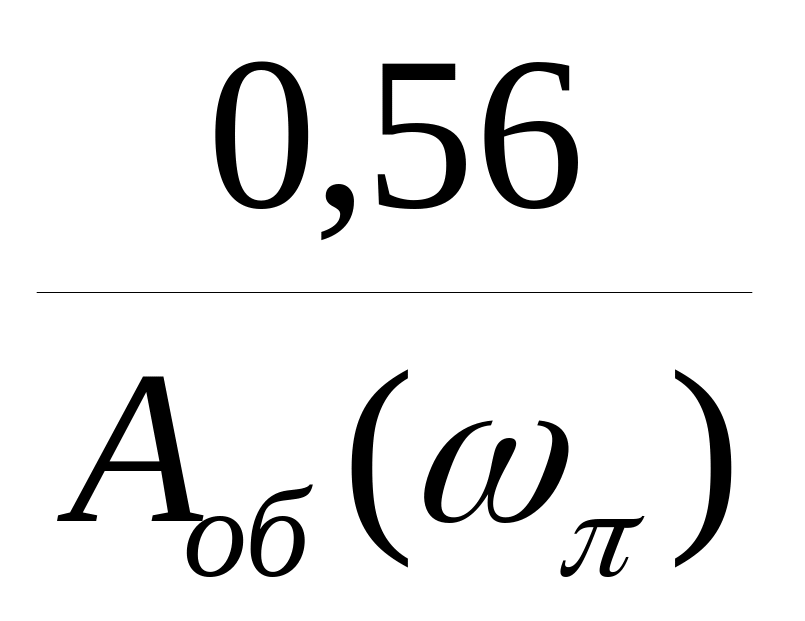

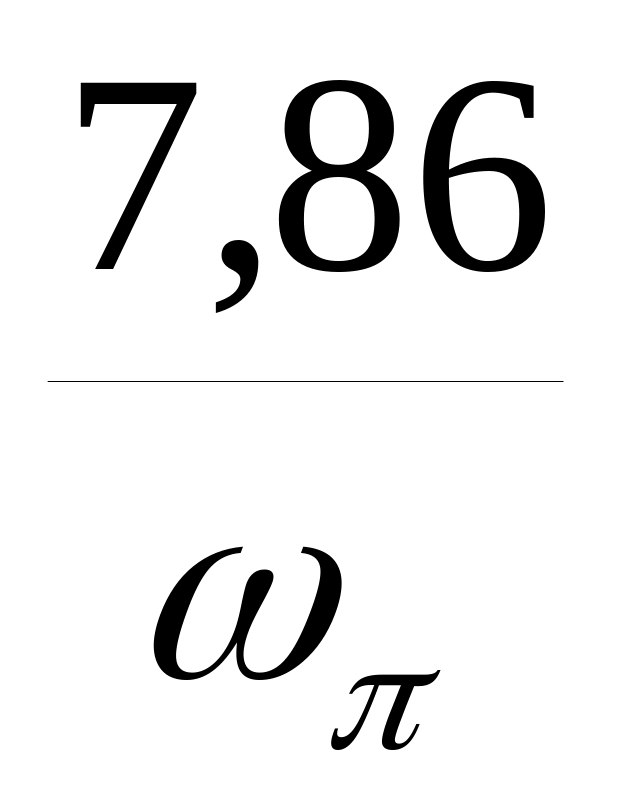
В таблице 12.2 обозначены:
![]() -
частота, при которой
-
частота, при которой
![]() ,
т.е. частота, при которой
пересекает
отрицательную вещественную полуось
комплексной плоскости;
,
т.е. частота, при которой
пересекает
отрицательную вещественную полуось
комплексной плоскости;
![]() -
модуль вектора
,
фаза которого
,
т.е. модуль вектора
,
соответствующего точке пересечения
с отрицательной вещественной полуосью
;
-
модуль вектора
,
фаза которого
,
т.е. модуль вектора
,
соответствующего точке пересечения
с отрицательной вещественной полуосью
;
- время запаздывания в объекте;
![]() - коэффициент
передачи астатического объекта
регулирования.
- коэффициент
передачи астатического объекта
регулирования.
Графо - аналитический расчет настроек АСР по запасу устойчивости, по модулю и фазе.
12.1.3.1. АСР с П и И - регуляторами
Если АФХ объекта имеет вид, показанный на рисунке 12.8. а,б, а необходимый запас устойчивости по модулю С и фазе , то можно записать следующее соотношение для П - регулятора (рис. 12.8 а).

 jV(ω)
jV(ω)
jV(ω)
jV(ω)

С С






 -1
А2
-1
-1
А2
-1
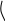
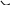

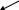 Д4
Д1
0
u(ω)
Д4
Д1
0
ω1
u(ω)
Д4
Д1
0
u(ω)
Д4
Д1
0
ω1
u(ω)

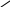

 А1
900
А1
900
Д2 Д3 Д2 Д3 ω2 А1

 Wоб(jω)
A2
Wоб(jω)
Wоб(jω)
A2
Wоб(jω)
а) П – регулятор б) И - регулятор
Рис.12.8.
![]()
![]()
![]()
Для И - регулятора (рис. 12.8 б)
![]()
![]() ;
;
![]()
где
![]() - коэффициент
передачи регулятора, обеспечивающий
запас устойчивости по модулю С;
- коэффициент
передачи регулятора, обеспечивающий
запас устойчивости по модулю С;
![]() - коэффициент
передачи регулятора, обеспечивающий
запас устойчивости по фазе ;
- коэффициент
передачи регулятора, обеспечивающий
запас устойчивости по фазе ;
![]() - коэффициент
передачи регулятора, обеспечивающий
запас устойчивости по модулю С и фазе
.
- коэффициент
передачи регулятора, обеспечивающий
запас устойчивости по модулю С и фазе
.
Эти соотношения позволяют найти параметры настройки П и И - регуляторов
(табл. 12.3)
Таблица 12.3
регулятор |
Параметры настройки П и И - регуляторов, при которых АСР выходит на границу заданного запаса устойчивости |
||
по модулю С |
по фазе |
по модулю С и фазе |
|
П
И |
|
|
|
12.1.3.2. АСР с ПИ - регулятором
Включение ПИ -
регулятора приводит к тому, что к каждому
вектору
![]() добавляется вектор
,
повернутый на 90º по часовой стрелке и
измененный по модулю в
добавляется вектор
,
повернутый на 90º по часовой стрелке и
измененный по модулю в
![]() раз (рис. 12.9).
раз (рис. 12.9).
Из рисунка 12.9 а
следует, что модуль
![]() АФХРС является гипотенузой
АФХРС является гипотенузой
![]() .
Гипотенуза любого прямоугольного
треугольника является диаметром
окружности, в которую вписан этот
треугольник. Это дает возможность найти
интересующие нас параметры настройки
Кр
и Ти с
помощью следующих построений.
.
Гипотенуза любого прямоугольного
треугольника является диаметром
окружности, в которую вписан этот
треугольник. Это дает возможность найти
интересующие нас параметры настройки
Кр
и Ти с
помощью следующих построений.
jV(ω)
 φpc(ωk)
φpc(ωk)



 0
Aоб(ωк)
u(ω)
0
Aоб(ωк)
u(ω)
 kpAоб(ωк)
kpAоб(ωк)
Ak
 Apc(ωk)
Apc(ωk)
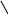 900
900
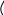

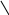 Bk
Bk

 Дк
Дк
![]()
Рис.12.9.
Запас устойчивости по модулю С (рис. 12.10).
Из рисунка 12.10 следует:
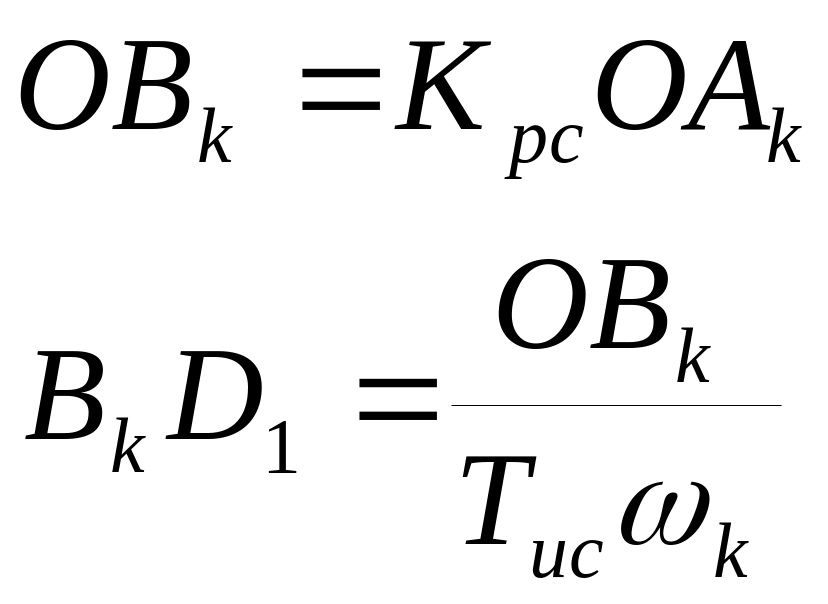
jV(ω)
С

 -1
0
-1
0

 Д4
Д1
u(ω)
Д4
Д1
u(ω)
Bk Аk
Wоб(jω)
Рис.12.10.
Отсюда
![]() ;
;
![]()
2. Запас устойчивости по фазе (рис. 12.11)
jV(ω)

 -1
-1


 Д4
0
u(ω)
Д4
0
u(ω)

 Д2
Ak
Д2
Ak
Ck Wоб(jω)
Рис.12.11.
В соответствии с рисунком 12.11
![]() ,
,
![]() ,
,
Отсюда
![]() ,
,
![]()
3. Запас устойчивости по модулю С и фазе (рис. 12.12)
jV(ω)
С
 -1
-1



 Д4
Д1
0
u(ω)
Д4
Д1
0
u(ω)

 Ak
Ak
Д2 Д3
Ek Wоб(jω)
Рис.12.12.
Из рисунка 12.12 имеем
![]() ,
,
![]()
Следовательно
![]() ;
;![]()
Расчетные соотношения сведены в таблицу 12.4.
Таблица 12.4
Параметры настройки ПИ – регулятора, при которых АСР выходит на границу заданного запаса устойчивости |
||
по модулю С |
по фазе |
по модулю С и фазе |
|
|
|
4. Далее по данным табл. 12.4 чертятся кривые границ заданного запаса устойчивости в плоскости параметров Кр-Ти, проводятся касательные к ним из начала координат и находятся оптимальные значения настроечных параметров Кропт и Тиопт (рис.12.13).
 Кр
Кр



![]()


 Крс
Крс
![]()

 Кр
Кр



 Крс
Крс
![]()
 0
Ти
0
Ти
![]()
![]()
![]()
Рис.12.13.
12.1.3.3. АСР с ПИД - регулятором
Включение
ПИД - регулятора приводит к добавлению
к векторам![]() векторов
,
повернутых на 90º по часовой стрелке и
измененных по модулю в
векторов
,
повернутых на 90º по часовой стрелке и
измененных по модулю в
![]() раз (рис. 12.14).
раз (рис. 12.14).
jV(ω)
φpc(ωk)
0 Aоб(ωк) u(ω)
kpAоб(ωк)
Ak
Apc(ωk)
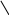 900
900
Bk

Дк
![]()
Рис.12.14.
Это позволяет находить настроечные параметры ПИД - регулятора с помощью графических построений (табл. 12.5), аналогичных случаю АСР с ПИ - регулятором.
Таблица 12.5
Параметры настройки ПИД - регулятора, при которых АСР выход на границу заданного запаса устойчивости |
||
по модулю С |
по фазе |
по модулю С и фазе |
С -1 0 Д1 Ак Вк Wоб(jω)
|
-1 0 Ak Д2 Ск Wоб(jω)
|
-1 С 0 Ак Д3 Ек Wоб(jω)
|
Построив по данным таблицы 12.5 границы заданного запаса устойчивости в плоскости параметров Кр-Ти (рис. 12.13),находят оптимальные значения настроек ПИД - регулятора.
Определение оптимальных настроек АСР с помощью расширенных АФХОР
Расширенная АФХ
При анализе
устойчивости с помощью критерия Найквиста
на к омплексную переменную передаточной
функции накладывалось ограничение
![]() .
.
Введем расширенное ограничение
![]()
где
![]() - степень колебательной устойчивости.
Этим поставлено условие, чтобы корни
характеристического уравнения АСР
располагались внутри контура АОВ
- степень колебательной устойчивости.
Этим поставлено условие, чтобы корни
характеристического уравнения АСР
располагались внутри контура АОВ
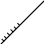
(рис. 12.15) комплексной плоскости или чтобы комплексная переменная Р передаточной функции изменялась по закону
![]()
jV(ω)
 B
B






![]()

 ωk
ωk

0 u(ω)
αk

A
Рис.12.15.
Частный случай передаточной функции, когда комплексная переменная ,
называют расширенной частотной функцией. Она может быть получена как отношение вынужденного движения на выходе из системы ко входному затухающему синусоидальному воздействию
![]()
При изменении получим расширенную АФХ.
В случаях ограничения с использованием критерия Найквиста находилась область устойчивого регулирования в плоскости параметров регулятора.
При ограничении совокупность настроечных параметров регулятора, соответствующая контуру АОВ (рис.12.15) в комплексной плоскости корней, образует внутри области устойчивости в плоскости параметров Кр-Ти линию равного затухания (т.е. линию заданной степени колебательной устойчивости).
Таким образом, расчет АСР на заданную степень затухания можно произвести, используя расширенную АФХ.
Расширенную АФХ записывают в виде:
![]() ,
,
где
![]() - расширенные вещественная, мнимая,
амплитудная и фазовая частотные
характеристики.
- расширенные вещественная, мнимая,
амплитудная и фазовая частотные
характеристики.
12.1.4.2. Расчетные соотношения
По аналогии с
условием границы устойчивости
![]() можно записать условие границы запаса
устойчивости в виде:
можно записать условие границы запаса
устойчивости в виде:
![]() ,
,
где
![]() -
расширенная АФХ разомкнутой АСР.
-
расширенная АФХ разомкнутой АСР.
Это равенство
означает наличие затухающих колебаний
с определенной степенью затухания
![]() .
.
Расширенная АФХРС может быть представлена в виде произведений соответствующих характеристик регулятора и объекта
![]()
Отсюда
![]()
или
![]()
и
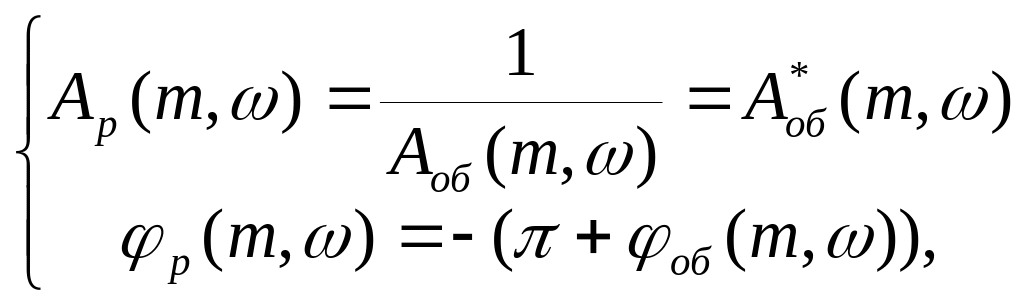
где
![]() -
расширенные АЧХ регулятора и объекта;
-
расширенные АЧХ регулятора и объекта;
![]() - расширенные ФЧХ
регулятора и объекта;
- расширенные ФЧХ
регулятора и объекта;
![]() - обратная расширенная АЧХ объекта;
- обратная расширенная АЧХ объекта;
![]() берется здесь по
абсолютному значению.
берется здесь по
абсолютному значению.
Решением системы уравнений относительно настроечных параметров
![]() ;
;
![]() ;
;
![]() (где
(где
![]() )
)
получены расчетные уравнения для определения настроек различных регуляторов.
Например, для ПИ - регуляторов
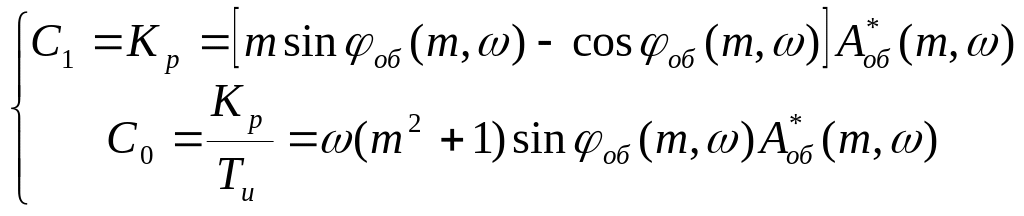
или
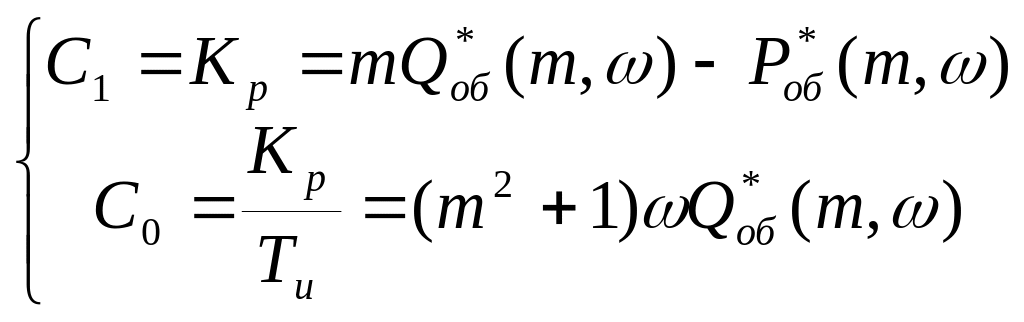
Здесь
![]() и
и
![]() - обратные расширенные вещественная и
мнимая частотные характеристики объекта
регулирования.
- обратные расширенные вещественная и
мнимая частотные характеристики объекта
регулирования.
Расчетные соотношения можно выразить и через обычные расширенные АФХ.
Подставив
![]()
и
![]() )
)
в уравнение границы заданного запаса устойчивости (через m)
![]() ,
,
получим расчетное уравнение в виде
![]()
![]()
Например, для ПИ – регулятора с передаточной функцией
![]()
![]()
подстановкой
![]() получим
получим

Отсюда
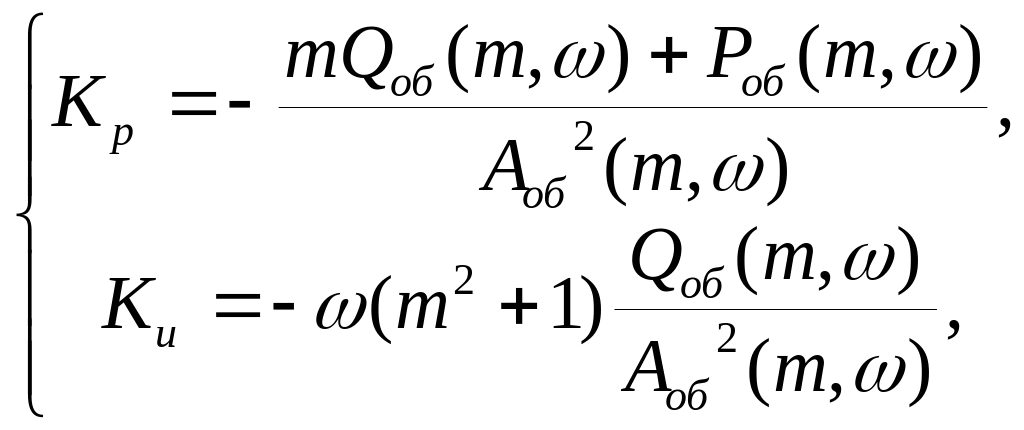
где
![]()
12.1.4.3. Порядок расчета
Из приведенных расчетных соотношений вытекает следующий порядок расчета настроек АСР:
Из передаточной функции
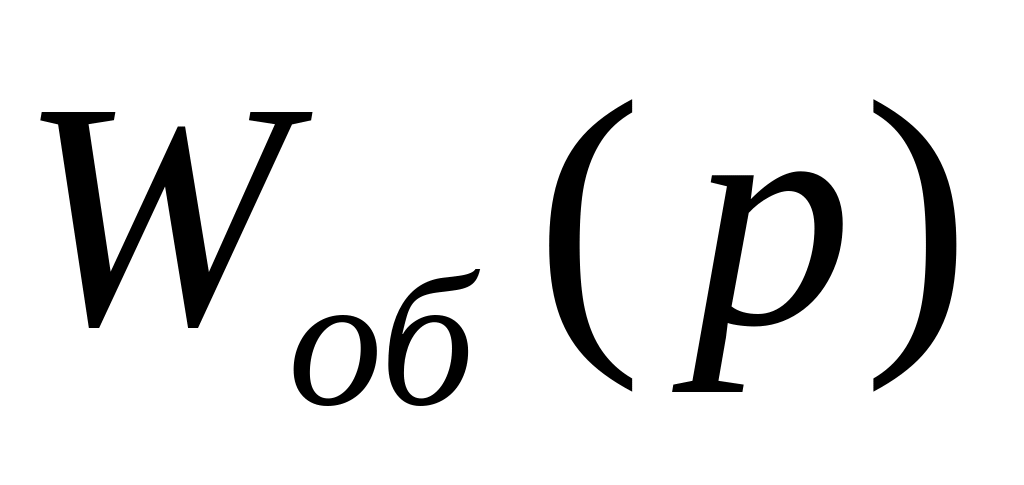 подстановкой
получают расширенные частотные
характеристики объекта:
подстановкой
получают расширенные частотные
характеристики объекта:
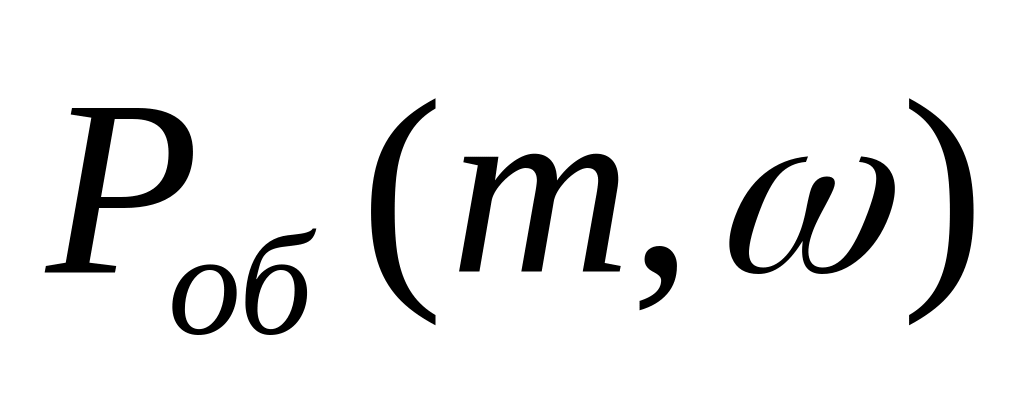 ,
,
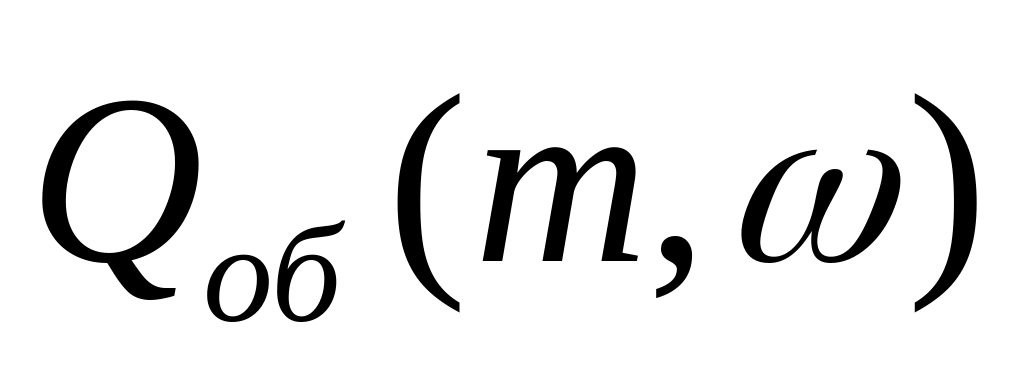 ,
,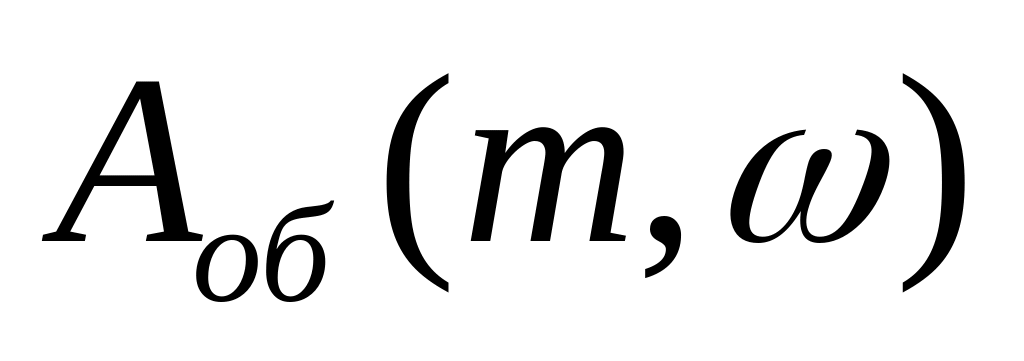 ,
,
, , , .
Подставляя в эти уравнения численные значения параметров объекта и выбранную величину m, получают
![]() ;
;
![]() .
.
В последние уравнения подставляют численные значения частоты от нуля до значения, при которым С0 становится отрицательной величиной.
Строят в координатах С0-С1 линию равной степени затухания

 в
виде совмещенного графика зависимостей
и
.Все
значения пар С0,С1,
соответствующие отдельным точкам линии
равной степени затухания (рис. 12.16),
обеспечивают заданную степень затухания
в
виде совмещенного графика зависимостей
и
.Все
значения пар С0,С1,
соответствующие отдельным точкам линии
равной степени затухания (рис. 12.16),
обеспечивают заданную степень затухания
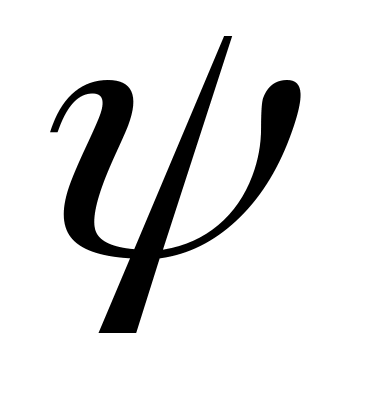 (заданную величину m)
(заданную величину m)
С0
ω1



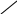 ω2
Ψзад=const
ω2
Ψзад=const
 ω0
ω0
ω3 Ψ<Ψзад

ω5
0 С1
Рис.12.16.
Выбор оптимальных значений С0 и С1.
Из рисунка 12.16 видно, что одну и ту же степень затухания можно получить при различном сочетании параметров настройки регулятора.
Однако, другие показатели качества регулирования (максимальное динамическое отклонение, степень перерегулирования, длительность переходного процесса ) при этом будут различными. На основе многочисленных расчетов переходных процессов для различных пар С0,С1 и экспериментальным путем установлено, что оптимальному процессу соответствует точка на кривой , лежащая "немного" правее и ниже максимума этой кривой.
Для более определенного выбора точки на кривой , соответствующей оптимальной настройке регулятора, следует на этом же графике линии построить кривую квадратичной интегральной оценки
![]()
Для этого значение интеграла следует представить в виде конечной суммы через амплитудно-частотный спектр переходного процесса
 ,
,
где
![]() -
АЧХ замкнутой АСР по каналу рассматриваемого
возмущения относительно регулируемой
величины;
-
АЧХ замкнутой АСР по каналу рассматриваемого
возмущения относительно регулируемой
величины;
![]() - частота среза.
- частота среза.
При этом значения интегрального критерия достаточно рассчитать для тех нескольких пар параметров, которые расположены на максимуме и справа от максимума кривой . Минимум этого интеграла и определит точку на кривой , соответствующую оптимальной паре настроек С0 и С1 (рис. 12.17).
 C0
C0
Ψзад=const


I

 Cопт
Cопт
Iмин


C1
Рис.12.17.
12.2. Переходные процессы (процессы регулирования) в замкнутой АСР