Решение.

1. Найдем D(y) из условия

D(y)=[0;1].

2. Найдем y’.

3. Решим уравнение - критическая точка.

Критические точки , в которых y’ не существуют не рассматриваем, т.к. они являются концами отрезка и будут рассматриваться отдельно.

4. 

5. 

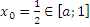
6. Найдем значения функции y на отрезке [0;1].

Ответ:

п.7 наибольшее и наименьшее значение функции f(x) на интервале.

Рассмотрим функцию y=f(x), определенную и дифференцируемую на (a;b), и найдем наибольшее или наименьшее значение функции на этом интервале.

Решение задачи основано на теореме: если дифференцируемая на (a;b) функция y=f(x) имеет на (a;b) единственный экстремум, то в случае, когда этот экстремум – максимум, y_max–наибольшее, а в случае минимума, y_min – наименьшее значение функции на интервале (a;b).

Пример. Найти наименьшее значение функции на интервале

Решение.

1. Найдем y’.

2. Решим уравнение

Получим

3. На интервале содержится единственная критическая точка

4. Построим на оси ОХ данный интервал и критическую точку

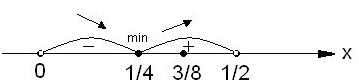
И определим знак y’ на каждом из двух полученных интервалов.

а) пусть в точке

б) пусть в точке

5. Так как в точке меняет знак с "-" на "+", то в точке функция имеет минимум.

6. Так как этот минимум является единственным минимумом на интервале , то в точке функция достигает наименьшего значения на этом интервале.

7. 

Ответ: .

п.8. Применение производной к нахождению оптимальных решений практических задач.

Пусть решение некоторой практической задачи сводится к нахождению наибольшего или наименьшего значений некоторой функции:

, (1)

аргументы которой x и y связаны дополнительным условием:

(2)

Для решения задачи, из равенства (2) находим значение и подставим его в (1). Получим функцию одной переменной

Из условия задачи или по виду функции Z находим D(Z). Если D(Z)=[a; b], то далее исследование проводится так, как в п.6. Если D(Z)=(a; b), дальнейшее исследование проводится так, как в п.7.

Функция (1) и условие (2) составляются по условию задачи.

Замечание 1. В некоторых случаях функцию (1) сразу можно получить в виде (4) без дополнительного условия (2).

Замечание 2. Аргументы функции (1) (x;y) могут обозначаться любыми буквами.

Пример. В прямоугольный треугольник с катетами a и b вписать прямоугольник наибольшей площади, имеющий общий прямой угол.

Решение.

Р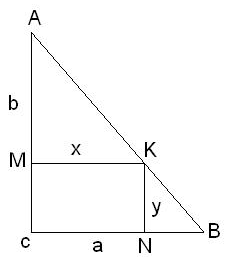 ассмотрим АВС , в котором С = , CB = a; AC = b. Пусть CMKN – вписанный прямоугольник. Найдем стороны прямоугольника наибольшей площади.

1) Пусть MK=x; KN=y.

Тогда площадь прямоугольника S=xy.

Найдем значения x и y, при которых S принимает наибольшее значение.

2) Найдем зависимость между x и y, исходя из того что четырехугольник вписан в данный треугольник. Так как AMK KNB, то

. Поэтому

3) Найдем y из этого выражения. Поделим почленно левую часть на у. Получим

Отсюда b(a – x) = ay или y = (a – x).

4) Подставим в функцию S = xy полученное значение у. Будем иметь функцию

5) Из чертежа видно, что x∈ [0;a] и нужно найти наибольшее значение функции S на отрезке [0;a].

6) Найдем

7) Найдем критические точки из уравнения S'=0 или . Отсюда

8)

9) Найдем значения функции на концах отрезка S(0)=0; S(a)=0/

Ответ: вписанный прямоугольник имеет наибольшую площадь