Министерство Образования Российской Федерации Северо-Кавказский горно-металлургический институт

(Государственный Технологический Университет)

Кафедра математики

Методические указания к типовому расчету по теме:

“Приложения дифференциального исчисления”

(для студентов ФИТ)

Владикавказ 2011

Составители: проф. Григорович Г.А.

Ст.пр. Дзеранова М.Т.

Ст.пр. Дадтеева А.М.

Асс. Соколова О.А.

Аннотация.

Данные методические указания должны помочь студентам ФИТ выполнить типовой расчет по одной из важнейших тем математического анализа “Приложения дифференциального исчисления”. Рассматриваются приложения производной к вычислению пределов функций, исследованию функции и построению ее графиков, нахождению оптимальных решений геометрических и физических задач.

Работа состоит из 2-х частей. В первой части приводятся краткие сведения из теории и решаются типовые задачи, аналогичные задачам, предлагаемым в дальнейшем для самостоятельного решения. Во второй части даются 30 вариантов задач для самостоятельного решения.

Введение

Предлагаемые методические указания должны помочь студентам ФИТ и ФЭТ выполнить типовой расчет по теме «Приложение производной». Этот раздел математического анализа исключительно важен в математическом образовании инженера, так как готовит теоретическую базу для решения многих технических задач.

Методические указания содержат необходимый теоретический материал и 30 вариантов индивидуальных заданий, каждый из которых состоит из 7 задач.

При составлении индивидуальных заданий учитывался современный взгляд на проблему и методику ее изучения. Так, например, в задании №6 студентам предлагается не только найти наибольшее и наименьшее значение функции на данном отрезке, но и на интервале, в некоторых случаях отрезок находится из дополнительных условий. Кроме того, предлагаются задачи с конкретным практическим содержанием.

Методические указания предназначены для студентов ФИТ и ФЭТ, но могут быть использованы при изучении темы «Приложение производных» на других факультетах, если несколько сократить число предлагаемых заданий в каждом варианте.

§1. Некоторые сведения из теории

п.1. Вычисление пределов с помощью производных.

Использование производных для вычисления пределов основано на теореме Лопиталя.

Теорема

Если f(x) и 𝜑(x) – функции, дифференцируемые в некоторой окрестности точки x₀ (за исключением, быть может, самой точки x₀) и при x→ x₀ обе эти функции одновременно стремятся к нулю или ∞, то, если существует

С помощью этой теоремы раскрываются неопределенности вида или .

Пример 1.

Ответ: 5.

Иногда теорему Лопиталя приходится применять несколько раз.

Пример 2.

Ответ: 0.

С помощью теоремы Лопиталя можно раскрывать не только неопределенности вида и , но и неопределенности других видов. Для этого с помощью тождественных преобразований данная неопределенность сводится к неопределенности вида или .

Пример 3.

Ответ: 1.

п.2. Исследование функции с помощью первой производной.

С помощью первой производной дифференцируемой функции y= f(x)можно находить:

1) промежутки возрастания и убывания функции;

2) точки максимума, минимума, а также максимальные и минимальные значения функции.

Чтобы решить эти задачи нужно:

1) найти область определения функции D(y);

2) найти производную y’= f’(x) и разложить ее на множители;

3) найти критические точки, т.е. точки, в которых f’(x)=0 или не существует;

4) нанести на числовую ось D(y) и критические точки функции, принадлежащие D(y);

5) определить знак y’ на каждом из полученных интервалов;

6) определить промежутки возрастания и убывания функции по правилу:

если при ∀ x∈(a; b) y’ >0, то f(x) возрастает на этом интервале; если же при ∀ x∈(a; b) y’<0, то f(x) убывает на данном интервале;

7) найти точки экстремумов функции по правилу:

если при переходе через критическую точку x₀ слева направо y’ меняет знак с “+” на “-“, то в т. x₀ - максимум, если y’меняет знак с “-“ на “+”, то в точке x₀ – минимум, если же y’ в точке x₀ не меняет знак, то экстремума в этой точке нет;

8) если нужно, найти значения функции в точках минимума и максимума y_max и y_min.

Замечание.

Область определения функции находится по следующим правилам.

1. Функция y= определена, если определены функции 𝜑(x) и f(x) и f(x)≠0

2. Функция определена, если определена функция f(x)и f(x)≥0

3. Функция определена, если определена функция f(x)и f(x)>0

4. Функция (А>0)определена, если определена функция 𝜑(x) и

5. Функция y = 𝜑(x)^f(x) определена, если определены функции 𝜑(x) и f(x )и

6. Функции y= arcsin f(x) и y=arcos f(x) определены, если определена функция f(x) и -1≤ f(x)≤ 1.

Пример.

Найдите промежутки возрастания, убывания и экстремумы функции

Решение.

1. Найдем D(y )из условия x– 2 ≥0, т.е. x≥2. Таким образом, D(y) = [2; +∞).

2. Упростим данную функцию и найдем ее производную:

3. Найдем критические точки, т.е. точки в которых

D= 16 + 84 = 100 = 10²

;

4. Нанесем на числовую ось D(y) и точку ∈ D(y)

5. Разложим производную на множители

И найдем знак y’ на каждом из полученных интервалов D(y), выбирая произвольные значения × на каждом из полученных интервалов и определяя знак у` в выбранной точке.

При

При = 3

6. Найдем промежутки возрастания и убывания функции

Так как при y’ < 0, то функция y убывает на

Так как при y’>0, то функция y возрастает на .

7. Так как при переходе через критическую точку слева направо производная меняет знак с “-“ на “+”, то — точка минимума данной функции.

8. 

Ответ: 1) — промежуток убывания; 2) — промежуток возрастания; 3) .

п.3. Исследование функции с помощью производной второго порядка.

С помощью производной второго порядка функции y = f(x)можно найти промежутки выпуклости, вогнутости и точки перегиба графика функции.

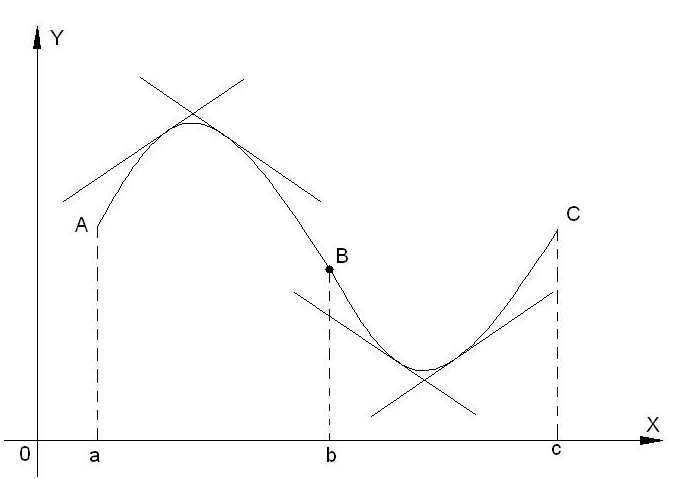
Определение 1. График функции y = f(x) называется выпуклым на (a;b), если он расположен ниже любой касательной, проведенной к нему на этом интервале.

Определение 2. График функции y = f(x)называется вогнутым на интервале (b;c), если он расположен выше любой касательной, проведенной к нему на этом интервале.

Определение 3. Точка x=b, отделяющая промежуток выпуклости от промежутка вогнутости называется точкой перегиба графика функции.

Правило.

Чтобы найти промежутки выпуклости, вогнутости и точки перегиба дважды дифференцируемой функции y = f(x) нужно:

1. Найти D(y);

2. Найти

3. Найти

4. Найти критические точки второго порядка, т.е. точки, в которых или не существует;

5. Нанести на числовую ось D(y) и критические точки второго порядка попадающие в D(y);

6. Найти знак на каждом из полученных интервалов;

7. Определить промежутки выпуклости и вогнутости, воспользовавшись теоремой.

Теорема 1.

Если функция y = f(x) дважды дифференцируема на (a;b) и при всех x∈ (a;b) f’’(x) <0 (f’’(x) >0),то график функции f(x) является выпуклым (вогнутым) на (a;b).

8. Найти точки перегиба графика функции пользуясь следующей теоремой.

Теорема 2.

Если функция y = f(x) дважды дифференцируема в окрестностях точки x₀ (за исключением, быть может, самой точки x₀) и при переходе через эту точку слева направо y’’меняет знак, то x₀ – точка перегиба графика функции.

Пример. Найти промежутки выпуклости, вогнутости и точки перегиба графика функции

Решение.

1. 

2. 

3. 

Окончательно получаем

4. Находим критические точки второго порядка, решая уравнение y’’=0

т.к. e^x≠0, то

— критические точки второго порядка.

Запишем

5. Нанесем на числовую ось D(y)=R и точки x₁ = -1 и x₂ = -3

6. Определим знаки y’’ на каждом из полученных интервалов, вычисляя значение у'' в точке соответствующего интервала

а) т.к. при , то при x∈ (-∞; -3) y’’>0.

б) т.к. при то при x∈ (-3;-1) y’’<0.

в) т.к. при то при x∈(-1; +∞) y’’>0.

7. По теореме 1 график функции является выпуклым на (-3;-1) и вогнутым на (-∞; -3) и (-1; +∞).

8. По теореме 2 точки x₁=-3 и x₂=-1 —точки перегиба графика функции.

Ответ: график является выпуклым при x∈(-3;-1) и вогнутым при x∈(-∞; -3) и (-1; +∞); точки x₁=-3 и x₂=-1 —точки перегиба.

п.4. Асимптоты графика функции.

В некоторых случаях, удаляясь от начала координат, график функции y=f(x), неограниченно приближается к некоторой прямой.

Эта прямая называется асимптотой графика функции. Асимптоты бывают вертикальными и наклонными.

1. Вертикальные асимптоты.

Если x=x₀ – точка бесконечного разрыва функции y=f(x), то прямая x=x₀ – вертикальная асимптота.

б) Наклонные асимптоты.

Наклонные асимптоты бывают правыми и левыми. К правой асимптоте неограниченно приближается график функции при его удалении от начала координат вправо.

К левой асимптоте график функции неограниченно приближается при его удалении от начала координат влево.

Правая асимптота имеет уравнение

где k и b–действительные числа, которые находятся по формулам:

Левая асимптота имеет уравнение

где k и b–действительные числа, которые находятся по формулам:

Если в уравнение (1) или (4) k=0, то соответствующая асимптота называется правой или левой горизонтальной асимптотой. Она имеет уравнение у=b

Пример 1. Найти асимптоты графика функции