3. Расчет методом «Контурных токов»

Произвольно задаемся направлением контурных токов в ячейках исходной схемы. Удобнее все токи указать в одном направлении – по часовой стрелке (рис. 4).

Составляем для каждого контура-ячейки уравнение по второму закону Кирхгофа, обходя контур по часовой стрелке.

Уравнение для первого контура:

–E₁ + E₂ = I_к1 · (R₁ + R₀₁ + R₂ + R₀₂ + R₄) – I_к2 · (R₁ + R₀₁) – I_к3 · R₄; (1.13)

уравнение для второго контура:

E₁ – E₃ = I_к2 · (R₁ + R₀₁ + R₃ + R₀₃ + R₅) – I_к1 · (R₁ + R₀₁) – I_к3 · R₅; (1.14)

уравнение для третьего контура:

0 = I_к3 · (R₄ + R₅ + R₆) – I_к1 · R₄ – I_к2 · R₅. (1.15)

Решаем составленные уравнения совместно как систему:

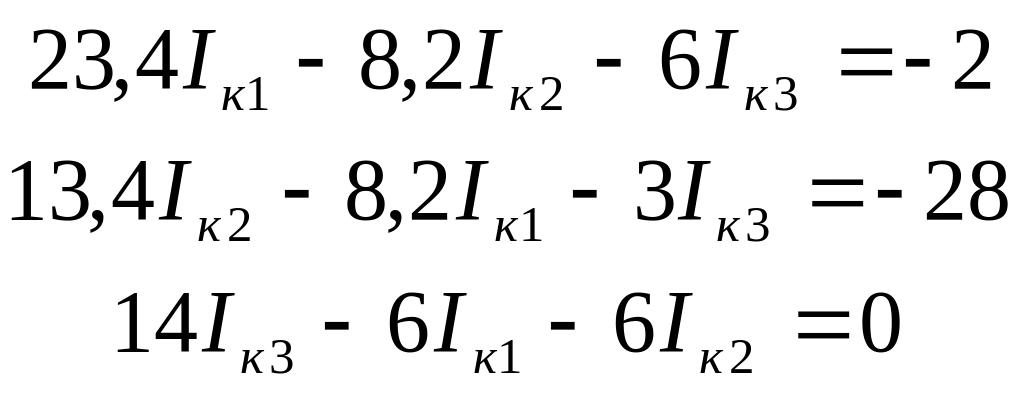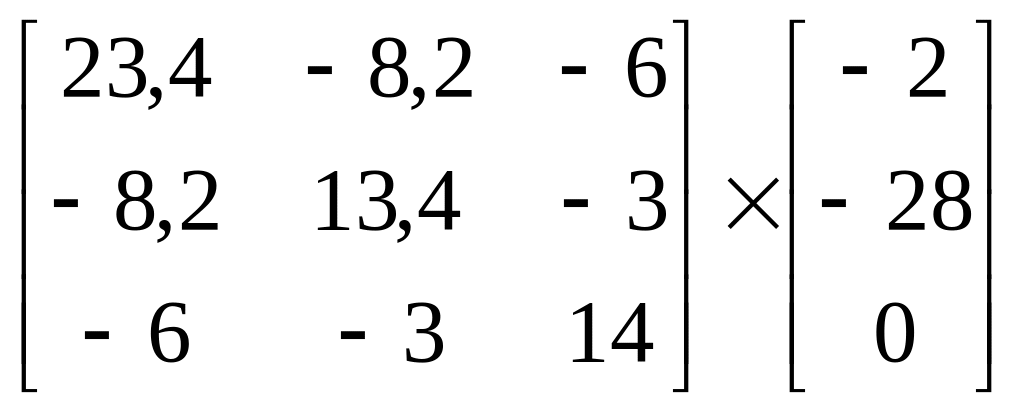=> (1.16)

Получаем значения контурных токов:

I_к1 = –1,65 А;

I_к2 = –3,42 А;

I_к3 = –1,44 А.

Если контурный ток оказался отрицательным, значит, его направление противоположно выбранному на схеме.

Токи во внутренних ветвях схемы I₁, I₄, I₅ определяются как сумма или разность соответствующих контурных токов. Если контурные токи в ветви совпадают по направлению, берется их сумма; если не совпадают, берется их разность:

I₁ = I_к2 – I_к1 = 3,42 – 1,65 = 1,77 А; (1.17)

I₄ = I_к1 – I_к3 = 1,65 – 1,44 = 0,21 А; (1.18)

I₅ = I_к2 – I_к3 = 3,42 – 1,44 = 1,98 А. (1.19)

Токи во внешних ветвях схемы I₂, I₃, I₆ равны соответствующим контурным токам:

I₂ = I_к1 = 1,65 А;

I₃ = I_к2 = 3,42 А;

I₆ = I_к3 = 1,44 А.

4. Баланс мощностей электрической цепи

При балансе мощностей алгебраическая сумма мощностей всех источников энергии должна быть равна алгебраической сумме мощностей всех приемников электрической энергии:

. (1.20)

Электрическая мощность P определяется по формуле:

. (1.21)

Для источника ЭДС, направление которой совпадает с направлением тока, мощность считается положительной:

. (1.22)

Если направления ЭДС и тока противоположны, то:

. (1.23 )

Для приемников электрической энергии, в частности для резисторов, мощность можно определить через величину сопротивления, заменив по закону Ома :

. (1.24)

Составим баланс мощностей:

,

,

(1.25)

Разность: 0,29.

5. Расчет потенциалов точек электрической цепи

Для расчета потенциалов точек внешнего контура данной электрической цепи выберем исходную точку О, от которой начнем расчет.

Таким образом, φ_О = 0. Относительно этой точки в направлении протекания тока рассчитываем потенциалы всех точек контура.

Если на участке между двумя точками включен источник питания, работающий в режиме генератора, то потенциал последующей точки будет больше потенциала предыдущей на величину напряжения этого источника:

φ_А = φ_О + (E₃ – I₃ · R₀₃) = 0 + (36 – 3,42 · 0.2) = 35,31 В. (1.26)

Если на участке между точками включен приемник электрической энергии, то потенциал последующей точки будет меньше потенциала предыдущей на величину падения напряжения этом участке:

φ_Б = φ_А – I₃ · R₃ = 35,31 – 3,42 · 2 = 28,47 В. (1.27)

Запишем уравнения потенциалов остальных точек цепи:

φ_В = φ_Б – I₆ · R₆ = 28,47 – 1,44 · 5 = 21,27 В; (1.28)

φ_Г = φ_В – (E₂ + I₂ · R₀₂) = 21,27 – (6 + 1,65 · 0.2) = 14,94 В; (1.29)

φ_Д = φ_Г – I₂ · R₂ = 14,94 – 1,65 · 9 = 0,09 В. (1.30)

Так как на участке между точками Д и О нет ни источников, ни приемников электрической энергии, то φ_Д = φ_О = 0.

Потенциальная диаграмма представляет собой график зависимости потенциалов точек цепи от величины сопротивлений участков между этими точками (рис. 5).

Потенциальная диаграмма строится в масштабе. По горизонтальной оси откладываются величины сопротивлений последовательно друг за другом по обходу контура. По вертикальной оси откладываются потенциалы точек.