13. Плоскорадиальный фильтрационный поток идеального газа по закону Дарси.

Плоскорадиальный фильтрационный поток имеет место в круговом пласте радиуса R_k, в центре которого имеется совершенная скважина радиусом r_c. Характеристики плоскорадиального фильтрационного потока:

1) Распределение пластового давления в потоке несжимаемой жидкости определяется:

(1)

А функция Лейбензона по формуле:

(2)

Подставив в (2) выражение функции Лейбензона P’=(_атP²)/2P_ат +С, получим закон распределения пласт. давления в плоскорадиальном фильтрационном потоке идеального газа: (3)

Сравнение кривых распределения давления в пласте в случаях установившейся плоскорадиальной фильтрации газа и несжимаемой жидкости при одинаковых граничных условиях показывает, что в газовом потоке имеет место резкое падение давления вблизи скважины и весьма малое вдали от нее.

2) Изменение градиента давления в зависимости от координаты r при плоскорадиальной фильтрации, несжимаемой жидкости описывается формулой

dP/dr=(P_k-P_c)/[r ln(R_k/r_c)] (4).

Градиент функции Лейбензона:

dP’/dr=(P_k’-P_c’)/[r ln(R_k/r_c)] (5).

Переходя от функции Лейбензона к давлению, получим

Следовательно, градиент давления вблизи забоя резко возрастает как за счет уменьшения r, так и за счет падения давления.

3) Дебит газовой скважины находим, подставив в формулу Дюпюи вместо объемного расхода несжимаемой жидкости Q массовый расход газа Qm и вместо давления P запишем функцию Лейбензона P’, тогда ;

Индикаторная линия при фильтрации газа имеет прямолинейный характер и строится в коор-тах Q_ат и Р²_к-Р²_с :

4) Скорость фильтрации газа (несжимаемой жидкости) определяется по формуле

В плоскорадиальном потоке газа также будет изменятся массовая скорость фильтрации, т.е.

Запишем это так:

5) Определим средневзвешенное по объему порового пространства пластовое давление в плоскорадиальном потоке газа.

Это давление определяется по формуле: , где V_п=mh(P_k²-P_c²) и dV_п=2rhmdr.

Давление в пласте определяется по формуле (3).

Подставим эти выражения в подинтегральное выражение:

Интегрируя данное выражение после преобразований получим следующее (*):

Если по формуле (*) провести расчеты для различных значений Р_к, Р_с, R_к, r_c, тоРР_к. Физически это объясняется значительной крутизной воронки депрессий.

14. Плоскорадиальный фильтрационный поток идеального газа по двучленному закону фильтрации.

Вблизи высокодебитных газовых скважин происходит нарушение закона Дарси, поэтому расчеты, связанные с разработкой газовых месторождений, а также с исследованием скважин проводят обычно по двучленному закону фильтрации. Считая фильтрацию плоскорадиальной, имеем уравнение:

(1)

Выразим скорость фильтрации при =_атP/Р_ат и Q_m=_атQ_ат:

W= Q_m/w=_атQ_ат/[_ат(Р/P_ат)2rh] = Q_атP_ат /2rhР (2).

Подставим (2) в (1), после разделения переменных получим (3):

1) Проинтегрируем (3) от забоя (Р_с, r_c) до произвольной точки пласта (P,r): получим

2) Интегрируя (3) от забоя до контура питания (P_k,R_k) и пренебрегая величинами 1/R_k по сравнению с 1/r_c, получим уравнение притока газа к скважине:

Обозначим ,

получим Р²_к – Р²_с = АQ_ат+BQ²_ат (4)

А и В – коэффициенты фильтрационных сопротивлений, определяются опытным путем по данным исследования скважин при установившихся режимах. При этом газовая скважина исследуется на 5-6 режимах, на каждом режиме измеряется дебит и определяется забойное давление. Затем скважину закрывают и давление в остановленной скважине принимают за контурное давление Р. После этого можно найти значения А и В. По результатам исследований строят индикаторную линию. Она представляет собой параболу, выпуклую к оси дебитов:

На практике удобнее применять (4) в виде :

(Р²_к – Р²_с)/ Q_ат = А+BQ_ат (5)

График этого уравнения, построенный в координатах Q_ат и (Р²_к – Р²_с)/ Q_ат, представляет собой прямую, для которой А-отрезок, отсекаемый на оси ординат, В-tg угла наклона прямой к оси абсцисс.

Уравнение притока газа к скважине (4) широко используется в расчетах при проектировании разработки газовых месторождений. По известному значению А определяют коллекторские свойства пласта.

15. Плоскорадиальный фильтрационный поток реального газа по закону Дарси.

Если пластовое давление ≥ 10 Мпа, а депрессия слишком мала, т.е. Р_с/Р_к  0,9, то уравнение состояния газа значительно отклоняется от уравнения состояния идеального газа и плотность определяется по формуле =_атz(P_ат)P/Р_атz(P). Для высоких пластовых давлений необходимо учитывать зависимость вязкости от давления =₀ exp [-a_ (P₀-P)] или при малых изменениях давления =₀ [1-a_(P₀-P)], где ₀ – вязкость при фиксированном давлении Р₀, a_ - коэффициент определяемый экспериментально и зависящий от свойства нефти и газа.

Если выполняется закон Дарси и фильтрация устанавливается, то справедливы ф-лы:

W_x= - kP/x; W_y= - kP/y; W_z= - (k /)(P/z + g).

В этом случае функция Лейбензона (обозн.’ро’большая):

Найдем дебит скважины при плоскорадиальном движении, используя аналогию между установившейся фильтрацией несжимаемой жидкости и газа напишем выражение для дебита, заменяя в формуле Дюпюи объемный дебит массовым, а величину k/ заменяем значениями функции Лейбензона, тогда

Перейдем к дебиту приведенному к атмосферному давлению (1):

По графикам зависимости z(P) и (P) определяем значения z(P_с)= z_с и z(P_к)= z_к, аналогично (P_с)= _с и (P_к)= _к. Заменим  и z постоянными z=(z_c+z_k)/2, =(_c+_k)/2, тогда ф-ла (1) примет вид:

Можно вычислить Р и приведенный дебит Q_ат по формуле (1), подставляя z=z₀ exp(-a_z(P₀-P)) и =₀exp(-a_(P₀-P)) где z=z(P)-величина, учитывающая сверхсжимаемость системы, а =(Р)- изменение вязкости.

16. Фильтрационный поток реального газа

по двучленному закону фильтрации к несовершенной скважине.

Уравнение притока реального газа по двучленному закону фильтрации к совершенной скважине

Для расчета дебитов газовых скважин несовершенных по степени и характеру вскрытия при нарушении закона Дарси можно предложить следующую схему. Круговой пласт, в центре которого находится скважина, делится на 3-и области.

1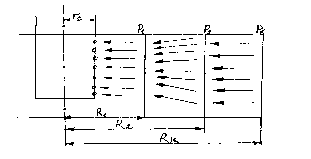 -ая область с R₁=(2-3)r_c. Из-за больших скоростей вблизи перфорационных отверстий нарушается закон Дарси, т.е. несовершенство по характеру вскрытия.

2-ая область – кольцевое пространство R₁<r<R₂, где R₂h. В этом случае линия тока искривляется из-за несовершенства скважины по степени вскрытия. Здесь справедлив двучленный закон фильтрации.

3-я область R₂<r<R_к - действует закон Дарси и течение жидкости плоскорадиальное.

Обозначим давления на границах областей через Р₁ и Р₂ можно записать для 3-ей области – ур-е(1):

Во 2-ой области h пласта переменна и изменяется от b при r=R₁ до h при r=R₂. Т.е. h(r)=+r, где  и  - определяются из условий h=b при r=R₁ и h(r)=h при r=R₂. Проинтегрируем ур-е

Получим ф-лу (2):

,

С₁ и C’₁ – коэффициенты, характеризующие несовершенство скважины по степени вскрытия, где

С₁=(1/ h)lnh + (1-h) ln(h/ R₁) /h, где h=b/h.

C’₁≈[(1/h²)-1](1/h), где b>>R₁.

В 1-ой области фильтрация происходит по двучленному закону, плоскорадиальное движение нарушается из-за перфорационных отверстий. Несовершенство по характеру вскрытия учитывается коэффициентами С₂ и С’₂, а распределение давления определяется по формуле (3):

,

С₂ определяется по графикам Щурова В.И., а для C’₂ формула C’₂  h²/3N²R³₀, где N – суммарное число перфорационных отверстий, R₀ – глубина проникновения перфорационной пули в пласт. Складывая почленно уравнения (1), (2), (3) получаем уравнение притока газа к несовершенной скважине:

,

Из этого уравнения можно выделить коэффициенты фильтрационных сопротивлений А и В:

17. Неустановившееся движение упругой жидкости в пористой среде.

Под упругим запасом жидкости в пласте понимается количество жидкости, которое можно извлечь из пласта при снижении давления в нем за счет объемной упругости пласта и насыщающих его жидкостей. Выделим элемент объема пласта V_о. Пусть V_ож – есть объем жидкости, насыщающий элемент пласта V_о при начальном давлении _о. Упругий запас жидкости будем определять по объему, замеряемому при начальном пластовом давлении. Обозначим через Δ Vз – изменение упругого запаса жидкости внутри объема пласта V_о при изменении давления во всех точках на величину Δp. Тогда Δ Vз определяется по формуле:

Δ Vз = _ж V_ож Δ p + _с V_о Δ p (1)

Учитывая, что начальный объем жидкости, насыщающий элемент объема пласта V_о, равен полному объему пор в этом элементе пласта, имеем:

V_ож = m V_о (2),

где m – коэффициент пористости, тогда равенство (1) с учетом (2) запишется:

Δ Vз = (m _ж + _с )V_о Δp (3) или Δ Vз = ^ V_о Δp (4),

где ^ = m _ж + _с (5) – коэффициент упругоемкости пласта. На основании (4) коэффициент упругоемкости пласта ^ численно равен изменению упругого запаса жидкости в единице объема пласта при изменении пластового давления в нем на единицу. Если (3) или (4) относить к разрабатываемому в условиях замкнутого упругого режима нефтяному месторождению, то под V_о следует понимать объем пласта, в котором к данному моменту времени давление изменилось на величину Δp, при этом: Δp = p_к – p , (6)

где p_к – начальное пластовое давление, а p - средне взвешенное по объему возмущенной части пласта V_о давление. Дифференцируя (4), имеем:

d (Δ Vз) = ^ d (V_о Δp).

С другой стороны, изменение упругого запаса жидкости в пласте за время dt равно объему отобранной жидкости, т.е.

d(ΔVз) = Q(t)dt , где Q(t) – дебит всех скважин, эксплуатирующих данную нефтяную залежь. Приравняв последние равенства, получаем дифференциальное уравнение истощения нефтяной залежи в условиях замкнутого упругого режима: Q(t)dt = ^ d (V_о Δp) (7).

Дифференциальное уравнение неустановившейся фильтрации упругой жидкости

Рассмотрим дифференциальное уравнение неустановившегося движения сжимаемой жидкости по закону Дарси, в деформируемой пористой среде при к=const (прониц.),=const (дин.вязкость):

(8)

P’- ф-я Лейбензона(‘ро’ большая).

Используем уравнение состояния упругой жидкости и упругой пористой среды:

= _о [1 + _ж (p – p_о)], m = m _о[1 + _c (p – p_о)],

_c – сжимаемость.

Перемножив эти уравнения, получим:

m=m_о _о +(m_о _о _ж + _о_c )(p–p_о)+_о _ж_c(p–p_о)² (9)

Последним слагаемым можно пренебречь ввиду его малости. Тогда, учитывая (5), имеем:

m = m_о _о [1 + ^(p – p_о) / m_о].

Дифференцируя это выражение по t, находим:

(10)

В этом случае функция Лейбензона (обозн. ‘ро’большая) для упругой жидкости имеет вид:

P’=(_о/^)+_о (p–p_о)= _о p + C ₁ (11)

Дифференцируя (11) дважды по координатам и складывая их, получаем:

² P’ = _о ² p (12)

В уравнение (8) подставим (10) и (12), имеем ур-е (13) :

где:  =k^/ - коэф-т пьезопроводности (вместо ‘хи’ надо писать ‘каппа’!!! ). Уравнение (13) является основным дифференциальным уравнением упругого режима фильтрации, которое называется уравнением пьезопроводности. Заметим, что коэффициент  - характеризует скорость перераспределения пластового давления при неустановившейся фильтрации упругой жидкости в упругой пористой среде. 0,1≤≤5 (м/с²)