4. Стационарное движение несжимаемой жидкости в пористой среде. Вывод дифференциального уравнения.

Полагаем пористую среду недеформируемой, т. е.  = const, μ = const (динамический коэф-т вязкости), K= const (коэф-т проницаемости) и m = const. При этом уравнение неразрывности примет вид:

Уравнение установившегося движения жидкости по закону Дарси имеет вид

Продифференцируем (2) по x, y, z соответственно:

Подставляя (3) в (1) получим

Используя оператор Гамильтона:

² Р = 0 или div grad P = 0 (5).

Уравнение (4) является дифференциальным уравнением установившейся фильтрации несжимаемой жидкости по закону Дарси в недеформируемой пористой среде. Это уравнение называют уравнением Лапласа. Удобнее ввести функцию

Ф (x, y, z) = К(Р+gz)/, называемую потенциалом скорости фильтрации. Тогда (2) примет вид:

Продифференцировав (6) и подставив в (1) получим

Т.е. потенциал скорости фильтрации, как и давление, удовлетворяет ур-ию Лапласа.

Заметим, что функции Р(x, y, z) и Ф(x, y, z), удовлетворяющие уравнению Лапласа, являются непрерывными, имеющими непрерывные частные производные второго порядка и называются гармоническими.

Р₁, Р₂, … ,Р_n – являются решениями уравнения (4), тогда функция Р = С_iP_i

(i = 1, … , n) также является решением уравнения Лапласа

5. Одномерные фильтрационные потоки несжимаемой жидкости в однородных пластах. Плоскорадиальный фильтрационный поток.

К одномерным относятся следующие фильтрационные потоки:

1) Прямолинейно параллельный фильтрационный поток.

2) Плоскорадиальный фильтрационный поток

3) Радиально-сферический фильтрационный поток.

Плоскорадиальный фильтрационный поток. Уравнение Лапласа в данном случае имеет вид: Это уравнение представим в цилиндрических координатах r и . Вследствие осевой симметрии характеристики потока не зависят от угла  и являются функциями только координаты r. Пусть ось цилиндра, радиус которого больше радиуса скважины r>r_с, совпадает с осью z. Тогда для плоскорадиального потока произвольная трубка тока с центральным углом  и площадью фильтрационной поверхности (r) = rh имеет следующий вид: (рис.1)

рис.1

r =R_k – S, dS = -dr. Тогда в соответствии с законом Дарси

Поскольку dQ/dr = 0 и имеем

Это и есть дифференциальное уравнение Лапласа в полярных координатах для установившегося плоскорадиального фильтрационного потока несжимаемой жидкости по закону Дарси. Проинтегрировав (1) получаем общее решение Р = С₁ lnr + C₂ (3), C₁ и C₂ находят из граничных условий Р = Р_с при r = r_с; Р = Р_к при r = R_k (4) Подставляя (4) в (3) находим давление Р_с = С₁ lnr_с + C₂ ; Р_к = С₁ lnR_k + C₂  C₁ = (P_k – P_c)/ln(R_k/r_c)

Подставляя С₁ и С₂ в (3) получим закон распределения давления в плоскорадиальном потоке:

Градиент давления dP/dr=C₁/r. С учетом C₁ = (P_k – P_c)/ln(R_k/r_c) получим:

Тогда скорость фильтрации и дебит скважины соответственно определяются по формулам

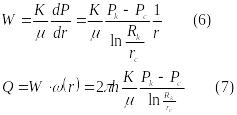Формулу (7) называют формулой Дюпюи, которая позволяет определить дебит скважины. Закон движения частиц жидкостей вдоль их траектории найдем из соотношения скорости фильтрации и средней скорости движения жидкости.

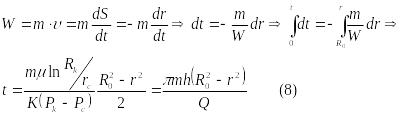
Где R₀ – начальное положение частицы жидкости в момент времени t = 0, r – текущее положение частицы жидкости в момент времени t. Время отбора Т всей жидкости из кругового пласта радиусом R_k получим, если в (8) подставим вместо R₀ = R_k; r = r_c : T = mh(R²_k – r²_c)/Q (9).

Вычислим средневзвешенное по объему порового пространства пластовое давление . Объем пор:

; ,

получим

Т. о. характеристики установившегося плоскорадиального потока несжимаемой жидкости в однородном пласте определяются по формулам (5) – (10).