Раздел VII. МоделиРование и теоретические основы разработки н/г месторождений.

1. Пористая среда и ее фильтрационная характеристика.

2. Скорость фильтрации. Закон Дарси. Границы применимости. Нелинейные законы фильтрации.

3. Моделирование процессов разработки. (Уравнения неразрывности, движения и состояния). Начальные и граничные условия.

4. Стационарное движение несжимаемой жидкости в пористой среде. Вывод дифференциального уравнения.

5. Одномерные фильтрационные потоки несжимаемой жидкости в однородных пластах. Плоскорадиальный фильтрационный поток.

6. Одномерные фильтрационные потоки несжимаемой жидкости в однородных пластах. Радиально-сферический установившийся фильтрационный поток.

7. Одномерные фильтрационные потоки несжимаемой жидкости при нелинейных законах фильтрации. Плоскорадиальный фильтрационный поток несжимаемой жидкости.

8. Исследование фильтрационных течений несжимаемой жидкости в неоднородных пластах. Плоскорадиальный фильтрационный поток несжимаемой жидкости. (Слоисто-неоднородный пласт, зонально-неоднородный пласт).

9. Интерференция скважин. Метод суперпозиции. Приток жидкости к группе скважин в пласте с удаленным контуром питания.

10. Интерференция скважин. Приток жидкости к скважине в пласт с прямолинейным контуром питания.

11. Приток к несовершенным скважинам.

12. Дифференциальные уравнения установившейся фильтрации упругой жидкости и газа по закону Дарси. Функция Лейбензона. Аналогия установившейся фильтрации сжимаемого флюида с фильтрацией несжимаемой жидкости. Установившаяся фильтрация упругой жидкости.

13. Плоскорадиальный фильтрационный поток идеального газа по закону Дарси.

14. Плоскорадиальный фильтрационный поток идеального газа по двучленному закону фильтрации.

15. Плоскорадиальный фильтрационный поток реального газа по двучленному закону Дарси.

16. Фильтрационный поток реального газа по двучленному закону фильтрации к несовершенной скважине.

17. Неустановившееся движение упругой жидкости в пористой среде. Подсчет упругого запаса жидкости в пласте. Дифференциальное уравнение неустановившейся фильтрации упругой жидкости.

18. Плоскорадиальный фильтрационный поток упругой жидкости.

ГЕОЛОГИЧЕСКОЕ МОДЕЛИРОВАНИЕ

19. Основные этапы построения геологической модели

20. Перечислить и дать определение фильтрационно-емкостных свойств по скважинам, необходимым для создания геологической модели

21. Методы интерполяции, используемые при построении различных карт свойств в модели

22. Перечислить и дать описание основных секций, заполняемых при создании геологической модели (на примере Irap RMS)

23. Методика ремасштабирования геологической модели, дать описание используемых алгоритмов осреднения

24. Подсчет запасов объемным методом в трехмерной геологической модели

ГИДРОДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ

25. Основные параметры, необходимые для создания гидродинамической модели

26. Определение трех видов проницаемости, задаваемых в модели. Использование кривых относительных фазовых проницаемостей при гидродинамических расчетах (в системе нефть-вода)

27. Физические свойства воды и нефти, определяемые в гидродинамической модели

28. Методика расчета ОФП в условиях отсутствия лабораторных исследований (Брукс-Корей)

29. Фетодика расчета ОФП в условиях отсутствия лабораторных исследований (Бурдайн)

30. Основные секции гидродинамической модели на примере Tempest MORE

1. Пористая среда и ее фильтрационные характеристики

Природные жидкости (нефть, газ и подземные воды) находятся в основном в пустотах, т.е. в порах и трещинах осадочных горных пород. Движение жидкостей, газов и их смесей через твердые тела по связанным между собой порам или трещинам называется фильтрацией. Пористая среда -множество твердых частиц тесно прилегающих друг к другу, сцементированных или несцементированных, пространство между которыми может быть заполнено жидкостью или газом. Пористая среда и насыщающие ее флюиды образуют сплошную среду, т.е. заполняют любой выделенный элементарный объем непрерывно.

Одной из важнейших характеристик пористой среды является пористость, измеряемая коэффициентом пористости Коэффициент пористости есть отношение объема пор (V_пор) в некотором элементе пористой среды ко всему объему V данного элемента и обозначается m, т. е. .

Н аряду с пористостью вводится понятие просветности, под которой понимается отношение площади просветов (_п ) в некотором сечении пористой среды по всей площади этого сечения (). Просветность измеряется коэффициентом просветности и обозначается через n, т.е

Коэффициент пористости одинаков для геометрически подобных сред, он не характеризует размеры пор и структуру порового пространства, поэтому для описания пористой среды вводят средний размер порового канала d или отдельного зерна пористого скелета. В теории фильтрации различают идеальные и фиктивные грунты. Под идеальным грунтом понимается модель пористой среды, поровые каналы которой представляют собой пучок тонких цилиндрических трубок капилляров с параллельными осями. Фиктивным грунтом называется модель пористой среды, состоящая из шариков одинакового диаметра. Простейшим геометрическим параметром, характеризующий размер порового пространства является эффективный диаметр частиц грунта d_эф, который определяется в результате механического анализа грунта.

2. Cкорость фильтрации. Закон Дарси. Границы применимости. Нелинейные законы фильтрации.

О сновной характеристикой фильтрационного движения является вектор скорости фильтрации w (вектор), который опр-ся след. образом(рис.1): Выберем произвольную точку М пористого пласта, через которую фильтруется жидкость, и проведем через нее элементарную площадку , через выделенную площадку в единицу времени протекает масса жидкости Q_m (элементарный массовый расход), тогда проекция вектора w на направление нормали n к выделенной площади дает: ,где  - плотность жидкости.

[w=1 м/с]. Действительное течение флюида в каждом живом течении пласта  осуществляется через суммарную площадь активных пор _n, поэтому имеем 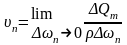(2).

Сравнивая последнее р-во с р-вом (1) и используя равенство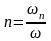 , а также условия р-ва пористости m и просветности n находим: 0<m<1 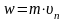 (3). Из р-ва (3) следует, что скорость фильтрации  меньше действительной средней скорости V течения флюидов. Основным соотношением теории фильтрации является закон фильтрации, названный именем Дарси, устанавливающий связь между вектором скорости фильтрации и полем давлений, которое вызывает фильтрационные течения: 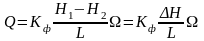(4), где Q –объемный расход жидкости через песчаный фильтр, длина которого L, а площадь поперечного сечения . Н = Н₁ – Н₂ – разность напоров воды над фильтром и у его основания, K_ф – коэффициент фильтрации (пропорциональности), зависящий как от структуры пористой среды, так и от свойств фильтрующейся жидкости.

При исследовании нефти, газа и их смеси формула Дарси записывается в виде 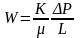(5), где  - динамическая вязкость. Р– приведенное давление, , К –коэффициент проницаемости, который не зависит от свойств жидкости и является динамической характеристикой только пористой среды. Из формулы (5) следует, что [К] =м².

Основные причины отклонения от закона Дарси:

1.Отклонения, связанные с проявлением инерционных сил, при высоких скоростях фильтрации (верхняя граница применимости закона Дарси) 2.Отклонения при достаточно малых скоростях фильтрации, вызванные проявлением не Ньютоновских реологических свойств жидкостей ее взаимодействием с твердым скелетом пористой среды (нижняя граница применимости)

1. Верхняя граница применимости закона Дарси.

Ее связывают с некоторым критическим значением числа Рейнольдса Re_кр. Число Рейнольдса определяется по формуле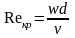 (6).Где d –некоторый характерный линейный размер пористой среды, =/ - кинематическая вязкость флюидов.

Для оценки границы применимости закона Дарси используется параметр Дарси, определяемый по формуле: 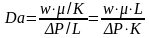(7)

Из формулы видно, что если справедлив закон Дарси, то Da=1 (8) Т.о равенство должно выполняться при условии, когда Re<Re_кр. При числах Re>Re_кр закон Дарси перестает быть справедливым. Для простейшего случая прямолинейно – параллельного течения двучленный закон фильтрации (9) имеет вид: Где -дополнительная const пористой среды, определяемая экспериментально, (/к)w - характеризует потери давления вследствие вязкости жидкости, (/к)w² – характеризует инерционную составляющую сопротивления движению жидкости, связанных с криволинейностью поровых каналов. Еще нелинейный закон фильтрации записывают в виде одночленной степенной формулы: (10), где 1<n2, с- параметр, определяется опытным путем.

2. Нижняя граница применимости закона Дарси

При малых скоростях течения природа нелинейности закона фильтрации иная, чем в области больших скоростей фильтрации. Она связана с проявлением неньютоновских свойств фильтрующих флюидов, а также других физико-химических эффектов. Наиболее простой нелинейный закон фильтрации неньютоновских жидкостей в основе которого лежит модель фильтрации с предельным градиентом имеет вид: (11),

где  - начальный градиент давления, по достижении которого начинается движение жидкости. При меньших значениях градиента движение отсутствует.