Течение однофазного потока в трубах

Движение однофазного потока (жидкость или пар при докритиче- ском давлении, теплоноситель при сверхкритическом давлении) описыва­ется уравнениями неразрывности (8.2), (8.3), движения (8.11), (8.12), (8.14), энергии (8.16), (8.18), (8.20), состояния, а также заданными начальными и граничными условиями.

Для использования уравнений состояния, показывающих зависи­мость р, v, с_р, ц и других параметров воды от температуры и давления потока, необходимо знать структуру потока, распределение температуры, давления и скорости потока по длине и сечению трубы. При проведении тепловых и гидравлических расчетов принимается, что давление в потоке по сечению постоянно, т. е. изменяется только по длине трубы.

Структура однофазного потока жидкости характеризуется непрерыв­ным гладким изменением плотности ее по сечению и длине трубы, а также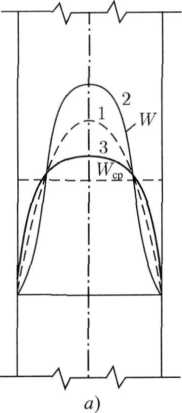

Р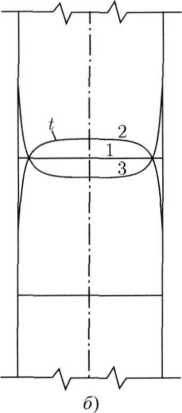 ис. 8.3. Распределение скорости (а) и температуры (б) однофазной жидкости в тру­бе: 1 — изотермическое движение; 2 — охлаждение жидкости; 3 — нагревание жид­кости.

во времени. При этом поля температуры и скорости потока тоже непрерыв­ны и гладки в пространстве и времени (рис. 8.3). В любой момент времени отдельная частица движущейся жидкости имеет определенную по величине и направлению скорость.

В одномерном приближении описания движения жидкости в трубе (по оси трубы) принимается, что температура и скорость потока постоянны по радиусу трубы (в ее сечении) и переменны по ее длине. Следовательно, температура и скорость потока усредняются по сечению трубы. При этом характеристика жидкости и потока также принимаются постоянными по сечению потока.

Характеристики течения однофазного потока в стационарных условиях

Из уравнений неразрывности (8.5) по известному расходу массы жид­кости G можно определить массовую скорость потока pw, кг/(м² сек):

Эта величина постоянна по длине трубы (при ее постоянном сече­нии /). Зная в каком-либо сечении трубы плотность жидкости р_ж, можно определить среднюю скорость ш_ж в этом сечении:

% = (рю)/р_ж. (8.26)

Для определения плотности жидкости р_ж по уравнению состояния р =

• pip, t) или р = р(р, К) необходимо рассчитать среднюю энтальпию по­тока /*_ж в данном сечении по известной величине энтальпии /ц_х на входе в трубу или ее участок. При этом используется уравнение (8.21):

К = h_BX + ■ I. (8.27)

pw - f

Давление р_ж в рассматриваемом сечении определяется по давлению на входе в трубу р_вх и перепаду давления на участке Др (8.14):

Рж ⁼ Рвх ^— Др.

Полученные значения р_ж, Н_ж используются для определения в данном сечении v, с_р, р, А и т. д.

При расчете перепада давления Др на участке длиной I необходимо знать среднеинтегральные значения плотности р_ср и удельного объема v_cp жидкости:

i I

(8.28)

Практически, средние значения плотности и объема воды и пара при докритическом давлении и водного теплоносителя вне зоны большой теп­лоемкости при сверхкритическом давлении можно определять по средней энтальпии потока Л_ср:

h_Cp = {h„ + h_K)/2,

где h_H, h_K — энтальпия потока в начале и конце участка, кДж/кг.

Средние значения плотности и объема в зоне большой теплоемкости (h = 1600 -г 2600 кДж/кг) определяется по формулам:

Рк^к ~ Pn^H ,Q _{ofl ч}

Рср = —т г ; (8.29,а)

h_K~h„

'Ун^-н /о то

v_Cp = —г ; > (8.29,6)

h_K Ни

^гДе р_к, р_н, ?;_к, у_н определяются по h_K и h„.