2.3. Уточнение корней методом касательных (метод Ньютона)

Метод касательных, связанный с именем Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Предположим, что функция f(x), имеющая корень v на отрезке [a,b], дифференцируема на этом отрезке, и её производная f’(x) не обращается на нем в нуль.

Возьмём произвольную точку x₀ отрезка [a,b] и запишем в ней уравнение касательной к графику функции f(x):

y=f(x₀)+ f’(x₀) (x- x₀).

Полагая в этом уравнении y=0, находим абсциссу x₁ точки пересечения касательной с осью Ox:

Повторим проделанную процедуру: напишем уравнение касательной к графику функции y=f(x) при x=x₁ и найдём для неё точку пересечения x₂ с осью Ох:

Продолжая этот процесс, получим последовательность {x_n}, определенную с помощью рекуррентной формулы

( 0)

Процесс вычисления продолжается до тех пор, пока не будет выполнено условие: |x_n+1 - x_n| < . При выполнении этого неравенства итерационный процесс уточнения корня следует прекратить и в качестве искомого приближенного значения корня x^* взять x^*= x_n+1. Реализация алгоритма метода касательных представлена на блок-схеме в прил. 3.

Геометрически с помощью этого метода предлагаем построить касательную к кривой y=f(x) в выбранной точке x=x_n, найти точку пересечения её с осью абсцисс и принять эту точку за очередное приближение к корню (рис.9).

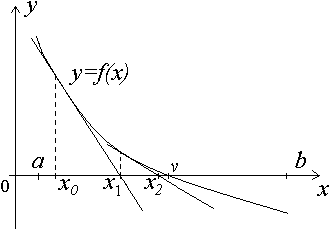
Рис. 9. Геометрическая иллюстрация метода касательных (метода Ньютона)

Очевидно, что этот метод обеспечивает сходящийся процесс приближений лишь при выполнении некоторых условий и при их нарушении либо дает расходящийся процесс (рис.10), либо приводит к другому корню (рис.11).

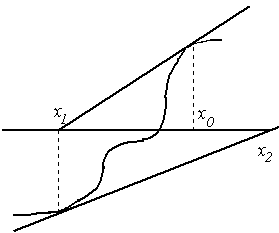
Рис. 10. Расходящийся процесс Рис. 11. Приближение к другому корню

Теорема (о сходимости метода касательных). Пусть функция f(x) дважды непрерывно дифференцируема на [a,b], причем её производные удовлетворяют неравенствам

| f ’(x)|m>0, | f ’’(x)|M, x[a,b].

Предположим, что корень x=v уравнения (1) является внутренней точкой отрезка [a,b], т.е. a<v<b. Тогда, найдется такое : 0<min(v-a,b-v), что при любом выборе начального приближения на отрезке [v-,v+][a,b] существует бесконечная итерационная последовательность (6) и эта последовательность сходится к корню v.

Обычно, на практике, за начальное приближение x₀ принимается такое значение из отрезка [a,b], для которого выполняется следующее условие:

f(x0) f ’’(x)>0.

( 0)

Чаще всего выбирают х₀=a или x₀=b в зависимости от того, для какой из этих точек выполняется условие (7).

Метод Ньютона эффективен для решения тех уравнений, для которых значение модуля производной |f'(x)| близ корня достаточно велико, т.е. график функции y=f(x) в окрестностях данного корня имеет большую крутизну.

Метод Ньютона является наиболее быстрым среди численных методов вычисления корня функционального уравнения. На практике необходимая точность достигается буквально после выполнения нескольких (не более 10) итераций.