2

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ»

Утверждено на заседании кафедры высшей математики 11.06.2011 г.

«Решение нелинейных уравнений средствами Microsoft Excel»

Методические указания и упражнения (для бакалавров 1-го курса)

Ростов-на-Дону

2011

УДК 621

Решение нелинейных уравнений средствами Microsoft Excel: методическое указания и упражнения(для бакалавров 1-го курса). – Ростов н/Д : Рост. гос. строит. ун-т, 2011. – 54 с.

Рассмотрены наиболее часто встречающиеся численные методы решения нелинейных уравнений: 1) метод половинного деления (дихотомии); 2) метод хорд; 3) метод касательных (метод Ньютона); 4) метод простых итераций, их реализация на Visual Basic for Application (VBA).

Лабораторные работы должны подготовить студентов к последующим этапам учебной деятельности – умению решать инженерные задачи с помощью персональных компьютеров. Задания содержат задачи по методам вычислений, с которыми сталкивается специалист, занимающийся конструкторской и расчетной деятельностью.

Электронная версия методических указаний находится в библиотеке, ауд. 224.

УДК 621

Составитель: канд. физ.-мат. наук, доц. В.В.Шамраева

Рецензент: канд. физ.-мат. наук, доц. Г.А.Власков

Редактор Т.М. Климчук

Доп. план 2011 г., поз. 189

Подписано в печать 12.07.11. Формат 6084/16. Бумага писчая. Ризограф.

Уч.-изд.л. 4,3. Тираж 20 экз. Заказ 391

Редакционно-издательский центр

Ростовского государственного строительного университета

344022, Ростов-на-Дону, ул. Социалистическая, 162.

Ó Ростовский государственный строительный университет, 2011 Введение

Рассматривается решение нелинейного уравнения

f(x)=0.

( 0)

Ясно, что любое нелинейное уравнение можно свести к виду (1).

Определение 1. Корнем уравнения (1) называется такое значение x=v аргумента, при котором это уравнение обращается в тождество, т.е. f(v)=0.

Корни уравнения (1) могут быть действительными и комплексными. В дальнейшем будет идти речь только о вычислении действительных корней. Геометрически корень уравнения (1) представляет собой абсциссу точки пересечения, точки касания или другой общей точки графика функции y=f(x) и оси Ox (рис. 1).

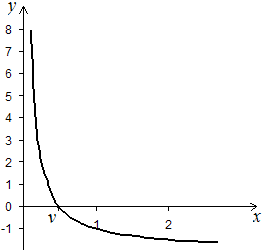
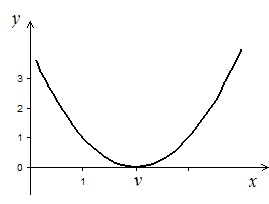
a) б) в)

Рис. 1. x=v – корень уравнения f(x)=0:

а) x=v – абсцисса точки пересечения графика функции y=f(x) и оси Ox;

б) x=v – абсцисса точки касания графика функции y=f(x) и оси Ox;

в) x=v – иной случай

Определение 2. Если функция f(x) имеет вид многочлена, то уравнение (1) называется алгебраическим.

Линейное, квадратное и биквадратное уравнения являются примерами алгебраических уравнений.

Приведём некоторые свойства алгебраических уравнений:

1. Всякое алгебраическое уравнение имеет по крайней мере один корень (действительный или комплексный).

2. Всякое алгебраическое уравнение n-й степени имеет не более n корней.

3. Всякое алгебраическое уравнение с действительными коэффициентами может иметь лишь четное число комплексных корней.

4. Всякое алгебраическое уравнение нечётной степени с действительными коэффициентами имеет по крайней мере один действительный корень.

Определение 3. Если f(x) включает в себя тригонометрические или экспоненциальные функции, то (1) называется трансцендентным, например xlg x = 1 или cos x = x³.

Решение квадратных и биквадратных уравнений, наипростейших тригонометрических и степенных, известно. Для кубических уравнений вводятся формулы Кардано. В общем же случае надежд на простое аналитическое решение нет. Более того, доказано, что даже алгебраическое уравнение выше четвертой степени неразрешимо в элементарных функциях. Итак, не всякое уравнение может быть решено точно. Однако в прикладных задачах это не является необходимым. К примеру, при изготовлении деталей многих точных механизмов допустимое отклонение от нормы измеряется тысячными долями миллиметра, или при измерении диаметра трубы газопровода допускается погрешность до 1 мм. Задачу отыскания корней можно считать практически решенной, если мы сумеем определить корни с заданной точностью .

В общем виде задача заключается в следующем:

Во-первых, установить, имеет ли уравнение (1) действительные корни, и если имеет, то сколько. Во-вторых, определить значение действительного корня уравнения (1) или точно (если это возможно и если имеет смысл), или с погрешностью, не превосходящей заданного, достаточно малого >0. Иными словами, если v[a,b] - истинное значение корня уравнения (1), т.е. f(v)=0, то требуется определить такое число x^*, что | x^*-v|<.

Методы решения нелинейных уравнений делятся на прямые и итерационные. Первые позволяют найти решение непосредственно с помощью формул и всегда обеспечивают получение точного решения x=v (примером такого рода является формула корней квадратного уравнения). В итерационных методах процедура решения задается в виде многократного применения некоторого алгоритма. Полученное решение x^* всегда является приближенным, хотя может быть сколь угодно близким к точному решению v. Итерационные методы наиболее универсальны и удобны для реализации на ЭВМ.

Основными, наиболее употребляемыми, итерационными методами решения нелинейных уравнений являются: 1) метод половинного деления (дихотомии); 2) метод хорд (метод секущих); 3) метод касательных (метод Ньютона); 4) метод простых итераций.

Алгоритм реализации любого итерационного метода состоит из двух частей:

1. отделение корней – отыскание некоторого приближенного значения корня или содержащего его отрезка (при этом выделяются области, содержащие только один корень, и рассматривается вопрос о кратности корней);

2. уточнение корня – построение итерационного процесса, позволяющего уточнить значение корня.

Что касается отделения корней, тут нет формальных методов, отрезки определяются или табуляцией, или исходя из физического смысла, или аналитическими методами. Уточнение корня выполняется различными итерационными методами, суть которых в последовательном уточнении начального приближения корня x₀ – x₁, x₂, … , x_n. Если значение x_i, i=1,2, … с ростом n приближается к истинному значению корня v, то процесс сходится. Выходом из итерационного процесса являются условия: |f(x_n)|<  и | x_n - x_n-1 |< . Всюду далее будем предполагать достаточным выполнения одного из этих условий. Это означает, что все функции в следующих далее лабораторных работах являются не слишком «крутыми» и не слишком «пологими» вблизи истинного корня.