
- •5.1 Общие понятия дифференциальных уравнений
- •5.2 Алгоритм решения дифференциальных уравнений с разделяющимися переменными
- •5.3 Алгоритм решения однородных дифференциальных уравнений 1-го порядка.
- •5.4 Алгоритм решения дифференциальных уравнений 1-го порядка, приводящихся к однородным дифференциальным уравнениям
- •5.5 Алгоритм решения линейных дифференциальных уравнений 1-го порядка
- •5.6 Алгоритм решения уравнений Бернулли
- •5.7 Алгоритм решения уравнений в полных дифференциалах
- •5.8 Линейные дифференциальные уравнения. Определения и общие свойства
- •5.9 Линейные однородные уравнения второго порядка с постоянными коэффициентами.
- •5.10 Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. ( специальная правая часть ).
5.8 Линейные дифференциальные уравнения. Определения и общие свойства
Дифференциальное
уравнение n
– го порядка называется линейным, если
оно является уравнением первой степени
относительно совокупности искомой
функции у
и её производных
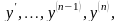 т.е. имеет вид
т.е. имеет вид
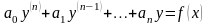 ,
(1)
,
(1)
где
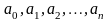 и f(x)
– заданные функции от х
или постоянные, причем
и f(x)
– заданные функции от х
или постоянные, причем
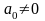 для всех значений х
из той области, в которой мы рассматриваем
уравнение (1).
для всех значений х
из той области, в которой мы рассматриваем
уравнение (1).
Если
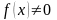 ,
то уравнение называется линейным
неоднородным
или уравнением
с правой
частью. Если
же
,
то уравнение называется линейным
неоднородным
или уравнением
с правой
частью. Если
же
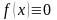 ,
то уравнение имеет вид
,
то уравнение имеет вид
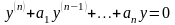 (2)
(2)
и называется
линейным однородным. Левая часть этого
уравнения является однородной функцией
первой степени относительно
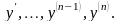
Основные свойства линейных однородных уравнений.
Теорема 1. Если y1 и y2 – два частных решения линейного однородного уравнения второго порядка
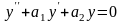 (3)
(3)
то y1 + y2 есть также решение этого уравнения.
Теорема 2. если y1 есть решение уравнения (3) и С – постоянная, то Су1 есть также решение уравнения (3).
Определение 2.
Два решения уравнения (3) y1
и y2
называются
линейно
независимыми
на отрезке
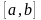 ,
если их отношение на этом отрезке не
является постоянным, т.е. если
,
если их отношение на этом отрезке не
является постоянным, т.е. если
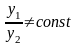 .
В противном случае решения называются
линейно
зависимыми.
.
В противном случае решения называются
линейно
зависимыми.
Определение 3. Если y1 и y2 суть функции от х, то определитель
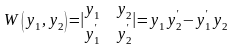
называется определителем Вронского или вронскианом данных функций.
Определитель Вронского имеет много различных свойств. Нам для доказательства теоремы об общем решении уравнения (3) потребуется следующее свойство:
Теорема 3.
Если определитель Вронского
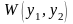 ,
составленный для решений y1
и y2
линейного однородного уравнения (3), не
равен нулю при каком-нибудь значении
x=x0
на отрезке
,
где коэффициенты уравнения непрерывны,
то он не обращается в нуль ни при каком
значении х
на этом отрезке.
,
составленный для решений y1
и y2
линейного однородного уравнения (3), не
равен нулю при каком-нибудь значении
x=x0
на отрезке
,
где коэффициенты уравнения непрерывны,
то он не обращается в нуль ни при каком
значении х
на этом отрезке.
Теорема 4. Если y1 и y2 – два линейно независимых решения уравнения (3), то
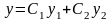 (5)
(5)
где С1 и С2 – произвольные постоянные, есть его общее решение.
5.9 Линейные однородные уравнения второго порядка с постоянными коэффициентами.
Имеем линейное однородное уравнение второго порядка
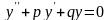 (7)
(7)
где p и q – постоянные действительные числа. Чтобы найти общий интеграл этого уравнения, достаточно, как было показано выше, найти два линейно независимых частных решения.
Будем искать частные решения в виде
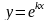 ,
где k
– const;
(8)
,
где k
– const;
(8)
тогда
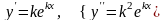 .
.
Подставляя полученные
выражения производных в уравнение (7),
находим:
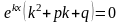 .
.
Так как
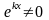 ,
то, значит,
,
то, значит,
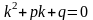 .
(9)
.
(9)
Следовательно,
если k
будет удовлетворять уравнению (7), то
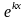 будет решением уравнения (7). Уравнение
(9) называется характеристическим
уравнением по
отношению к уравнению (7).
будет решением уравнения (7). Уравнение
(9) называется характеристическим
уравнением по
отношению к уравнению (7).
Характеристическое
уравнение есть квадратное уравнение,
имеющее два корня:
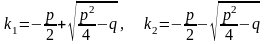 .
.
Возможны следующие случаи:
1)
 k1
и k2
– действительные и притом не равные
между собой числа
k1
и k2
– действительные и притом не равные
между собой числа
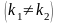 ;
;
2) k1
и k2
– действительные равные числа
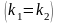 .
.
3) k1 и k2 – комплексные числа;
1) Корни характеристического уравнения действительны и различны: .
Следовательно,
общий интеграл имеет вид
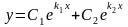 .
.
Корни характеристического уравнения действительны и равные: .
Поэтому общим
интегралом будет функция
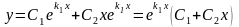 .
.
3) Корни характеристического уравнения комплексные. Так как комплексные корни входят попарно сопряженными, то обозначим:
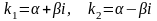
Следовательно, общее уравнение (7) в случае комплексных корней характеристического уравнения имеет вид
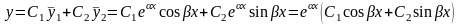 .
.
