
- •5.1 Общие понятия дифференциальных уравнений
- •5.2 Алгоритм решения дифференциальных уравнений с разделяющимися переменными
- •5.3 Алгоритм решения однородных дифференциальных уравнений 1-го порядка.
- •5.4 Алгоритм решения дифференциальных уравнений 1-го порядка, приводящихся к однородным дифференциальным уравнениям
- •5.5 Алгоритм решения линейных дифференциальных уравнений 1-го порядка
- •5.6 Алгоритм решения уравнений Бернулли
- •5.7 Алгоритм решения уравнений в полных дифференциалах
- •5.8 Линейные дифференциальные уравнения. Определения и общие свойства
- •5.9 Линейные однородные уравнения второго порядка с постоянными коэффициентами.
- •5.10 Линейные неоднородные уравнения второго порядка с постоянными коэффициентами. ( специальная правая часть ).
5.1 Общие понятия дифференциальных уравнений
Уравнение, содержащее хотя бы одну из производных у', у'', у''',… неизвестной функции у = у(х), называется дифференциальным уравнением для этой функции. Сама функция у и её аргумент х могут входить, а могут и не входить в дифференциальное уравнение. Порядок старшей производной, входящей в дифференциальное уравнение, называется порядком этого уравнения.
Таким образом, F(х; у; у') = 0 - общий вид дифференциального уравнения первого порядка;
F(х; у; у'; у'') = 0- общий вид дифференциального уравнения второго порядка, и т.д.
Решением (частным решением) дифференциального уравнения на некотором промежутке [a; b] оси ох называется функция, удовлетворяющая для всех х є [a;b] дифференциальному уравнению, то есть обращающая его в тождество (верное числовое равенство 0=0). Графики частных решений у = f(х) дифференциального уравнения называется его интегральными кривыми.
Решить дифференциальное уравнение (любого порядка) – это значит найти все его частные решения, то есть найти все функции у = f(х), удовлетворяющие этому уравнению. Формула, содержащая все (или почти все) частные решения дифференциального уравнения, называется его общим решением. Частные решения, не содержащиеся в общем решении, называются особыми решениями дифференциального уравнения.
5.2 Алгоритм решения дифференциальных уравнений с разделяющимися переменными
Это – дифференциальные уравнения вида
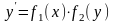 (6)
(6)
Решение таких уравнений производится по следующей схеме.
Сначала находим такие числовые значения
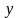 ,
при которых
,
при которых
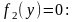
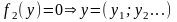 (7)
(7)
Функции
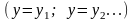 являются, очевидно, частными решениями
уравнения (6), ибо при подстановке каждой
из них в это уравнение получим тождество
0=0.
являются, очевидно, частными решениями
уравнения (6), ибо при подстановке каждой
из них в это уравнение получим тождество
0=0.
2) Теперь находим
все остальные решения
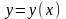 уравнения (6), для которых
уравнения (6), для которых
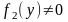 .
Делаем это по схеме:
.
Делаем это по схеме:
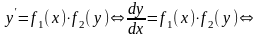
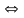 |
разделим выражения с х
и у
(разделим переменные х
и у))
|
|
разделим выражения с х
и у
(разделим переменные х
и у))
|
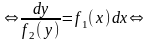 |
интегрируем обе части |
|
интегрируем обе части |
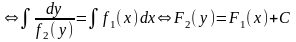 (8)
(8)
Полученное равенство
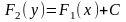 представляет собой общее решение
уравнения (6) в неявном виде (его общий
интеграл). Если в нем можно выразить
,
приводим его к явному виду
представляет собой общее решение
уравнения (6) в неявном виде (его общий
интеграл). Если в нем можно выразить
,
приводим его к явному виду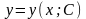 .
.
5.3 Алгоритм решения однородных дифференциальных уравнений 1-го порядка.
Это – дифференциальные уравнения вида
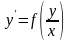 (9)
(9)
Такие уравнения
сводятся к уравнениям (6) с разделяющимися
переменными после введения новой
известной функции
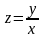 .
Действительно, пусть
.
Действительно, пусть
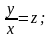 тогда
тогда
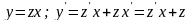 (10)
(10)
С учетом равенств (10) уравнение (9) примет вид:
 (11)
(11)
А это - уравнение
вида
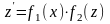 при
при
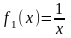 и
и
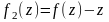 ,
то есть уравнение с разделяющимися
переменными для новой неизвестной
функции
,
то есть уравнение с разделяющимися
переменными для новой неизвестной
функции
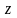 .
Найдя все его решения
.
Найдя все его решения
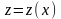 ,
затем по формуле
,
затем по формуле
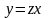 найдем и все решения
исходного
уравнения (9).
найдем и все решения
исходного
уравнения (9).
5.4 Алгоритм решения дифференциальных уравнений 1-го порядка, приводящихся к однородным дифференциальным уравнениям
Если дифференциальное
уравнение первого порядка F(х;
у; у') = 0 задано
вместе с начальным для него условием
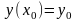 ,
то говорят,
что для этого уравнения задана задача
Коши:
,
то говорят,
что для этого уравнения задана задача
Коши:
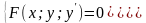 (1)
(1)
Решить её - это
значит найти те частные решения
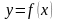 дифференциального уравнения F(х;
у; у') = 0 ,
которые еще удовлетворяют и заданному
начальному условию
.
дифференциального уравнения F(х;
у; у') = 0 ,
которые еще удовлетворяют и заданному
начальному условию
.
Схема решения задачи Коши (1) такова:
1. Решаем
дифференциальное уравнение F(х;
у; у') = 0 и
находим все его решения. То есть находим
общее решение (общий интеграл)
и возможные особые решения
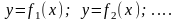 .
.
2. Подставляем начальные значения х = х0 и у = у0 в общее решение и находим соответствующее значение (значения) константы С:
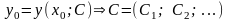 (2)
(2)
3. Подставляем каждое из найденных значений С в общее решение и получаем частные решения
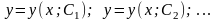 ,
,
являющиеся решением задачи Коши. Это те решения этой задачи, которые выделяются из общего решения дифференцированного уравнения F(х; у; у') = 0.
4. Проверяем, нет ли среди особых решений дифференциального уравнения F(х; у; у') = 0 таких, которые удовлетворяют начальному условию у(х0) = у0. Если такие найдутся, они тоже будут решениями задачи Коши (1).
