Анализ роста модельных деревьев методом аналитического дифференцирования после воздействия хозяйственных мероприятий
Метод аналитического дифференцирования позволяет анализировать рост древесных пород как интегрального показателя воздействия среды обитания на растение, в любом возрасте, после любых лесохозяйственных мероприятий, которыми могут быть все виды уходов за главной породой, рубки главного пользования, воздействие на плодородие почвы. Влияние антропогенных факторов (рекреация, промышленное и транспортное загрязнение воздуха и почвы) на рост деревьев также может быть выявлено на основании данной методики.
Использование дифференцирования в анализе роста было предложено доцентом кафедры лесоводства МарГТУ Е.И.Успенским и его дипломником С.Ф.Тузеевым (1974) для изучения динамики роста ели, произрастающей на вырубках, под пологом леса в затененных условиях и отзывчивости её на изменение освещенности в результате рубок ухода.
По мнению авторов, наиболее полная характеристика динамики роста древесных пород может быть дана на основании двух параметров:
накопленного результата изучаемого параметра (высота, диаметр, объем, масса);
скорости изменения этих параметров во времени (годичные или периодические приросты высоты, диаметра, объема, массы).
Сравнение кривых роста и скорости роста между контролем и опытом позволяет выявить происшедшие изменения. Выравнивание кривых роста с целью получения дальнейшего расчета первой (скорости роста) и второй (ускорения роста) производных проводится по полиномиальной модели третьего порядка: Y=a+bX+cX2+dX3 .
Первая производная (скорость роста): y`=b-2c-3dx2 .
Вторая производная (ускорение роста): y``=c+2dx
Математические методы сравнения статистических показателей, известные в математической статистике (см. п. 6.1, 6.4), позволяют обнаружить существенность различия.
Методика сбора полевого материала для изучения, например, роста сосны после прочисток в лиственно-хвойных молодняках следующая.
Для получения достоверных результатов необходимо проследить рост сосны после ухода на протяжении не менее чем 5 лет.
На участках после рубки и контроле (без рубки) отбираются учетные деревья – каждое пятое (десятое или пятнадцатое) - в количестве не менее 10…15 экземпляров.
У каждого учетного дерева измеряются годичные приросты высоты за годы после рубки и за три года до рубки. Годичный прирост определяют, измеряя линейкой расстояние между мутовками. Точность приростов в 1 см считается достаточной. На высоких деревьях приросты определяются шестом с нанесенными на нем делениями. Результаты измерения записывают в специальную ведомость (табл. 8.7).
Таблица 8.7
Полевая ведомость измерения текущего прироста высоты _______________ (см)
(порода)
Номер учетного дерева |
Годы |
|||||||
2005 (8) |
2004 (7) |
2003 (6) |
2002 (5) |
2001 (4) |
2000 год ухода (3) |
1999 (2) |
1998 (1) |
|
На участке (пробной площади) |
||||||||
1 |
28 |
20 |
15 |
16 |
12 |
10 |
9 |
9 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Под пологом на контроле |
|||||||
1 |
15 |
13 |
14 |
11 |
10 |
9 |
10 |
10 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эмпирическую линию регрессии необходимо выровнять. Эта работа проводится на ПК с использованием стандартного пакета Excel. Для этого открывают пакет Excel, заносят в таблицу данные приростов строго по годам. Используя «мастер построения диаграмм» и вкладку «график», выбирают вид графика: «график отображает развитие процесса во времени или по категориям». Далее выполняют построение диаграммы. После этого на график добавляют линию тренда, для чего стрелку курсора подводят на линию графика и щелкают правой кнопкой «мыши». Из открывшегося меню выбирают «Добавить линию тренда…». Далее выбирают полиномиальный тренд и указывают третью степень, после чего нажимают кнопку Ok. Выделяют линию тренда и в папке «Формат линии тренда» открывают вкладку «Параметры». Устанавливают флажки «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации R^2», после чего нажимают кнопку Ok. На диаграмме появятся уравнение с коэффициентами и показатель R2.
Пример. Получены следующие модели (табл. 8.8).
Таблица 8.8
Коэффициенты моделей приростов высоты учетных деревьев
Секция |
Коэффициенты модели y=a+bx+cx2+dx3 |
|||
a |
b |
c |
d |
|
На пробной площади |
6,4286 |
2,5851 |
-0,6223 |
0,0783 |
На контроле |
12,357 |
-2,8409 |
0,7565 |
-0,0455 |
На основании математических моделей рассчитываются «Выровненные Zh, см» на опытной и контрольной секциях (табл. 8.9). Для их расчета следует использовать тот же пакет Excel.
Скорость роста и ускорение роста (столбцы 4 и 5, 8 и 9) вычисляются по приведенным формулам первой и второй производных. Значению «x» соответствует порядковый номер года приростов (1, 2, 3 и т.д.). Коэффициенты a, b, c, d являются коэффициентами вычисленной полиномиальной математической модели третьей степени.
Построение графиков (рис. 8.6) выполняется, как правило, по трем показателям:
динамика изучаемого параметра во времени или средние годичные приросты модельных деревьев на секции с уходом и конт-роле (А);
Таблица 8.9
Параметры приростов сосны, скорости и ускорения её роста на пробной площади
Годы, x |
На опытной секции |
На контрольной секции |
||||||
Zh, см на "Пробе" |
выровненные Zh, см |
скорость роста y`=b-2c-3dx2 |
ускорение роста y``=c+2dx |
Zh, см на "К" |
выровненные Zh, см |
скорость роста y`=b-2c-3dx2 |
ускорение роста y``=c+2dx |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
1 (1998) |
9 |
8,4697 |
1,5754 |
-0,4657 |
10 |
10,2271 |
-1,4644 |
0,6655 |
2 (1999) |
9 |
9,736 |
2,2801 |
-0,3091 |
10 |
9,3372 |
-1,8739 |
0,5745 |
3 (2000) |
10 |
10,6973 |
3,4546 |
-0,1525 |
9 |
9,4143 |
-2,5564 |
0,4835 |
4 (2001) |
12 |
11,8234 |
5,0989 |
0,0041 |
10 |
10,1854 |
-3,5119 |
0,3925 |
5 (2002) |
16 |
13,5841 |
7,213 |
0,1607 |
11 |
11,3775 |
-4,7404 |
0,3015 |
6 (2003) |
15 |
16,4492 |
9,7969 |
0,3173 |
14 |
12,7176 |
-6,2419 |
0,2105 |
7 (2004) |
20 |
20,8885 |
12,8506 |
0,4739 |
13 |
13,9327 |
-8,0164 |
0,1195 |
8 (2005) |
28 |
27,3718 |
16,3741 |
0,6305 |
15 |
14,7498 |
-10,0639 |
0,0285 |
Примечание. Серым цветом обозначены данные измерений и расчетов на год проведения мероприятия.
Год ухода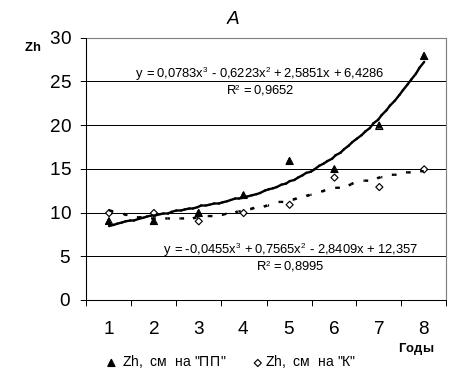
Б
В
Рис. 8.6. Динамика параметров роста сосны в высоту на секции с уходом («ПП»)
и без ухода – «контроль» («К»):
А - средние годичные приросты (Zh) модельных деревьев;
Б – скорость роста сосны на секциях с уходом и контрольной;
В – ускорение роста сосны по высоте
кривые, отражающие изменение величины средних текущих годичных приростов или скорость роста изучаемой древесной породы на секциях с уходом и контроле (Б);
кривые, отражающие ускорение роста изучаемой древесной породы на секциях с уходом и контроле (В).
При анализе графического материала необходимо обратить особое внимание на различия в росте деревьев, сделать вывод о лесоводственной эффективности проведенных рубок, а также о том, через сколько лет после рубок начинает проявляться их положительное воздействие на главную породу.
Если существенных изменений в росте после рубок не наблюдается, то, очевидно, должны быть внесены предложения по изменению режима рубок ухода в молодняках (сроки начала ухода, интенсивность выборки, период повторяемости). На основе различий роста во времени дается заключение о необходимости проведения очередного приема ухода.
Описанный метод может быть использован при анализе лесовод-ственной эффективности любых лесохозяйственных мероприятий или иных воздействий на насаждения, древостой, почву или лесорастительные условия. Это могут быть внесение удобрений в почву, гидромелиорация, применение различных методов лесоводственных уходов за лесом, любое антропогенное влияние, включая рекреационное воздействие или пастьбу скота. Точно также данный прием анализа может быть полезен при сравнении роста главной породы в разных типах леса и типах лесорастительных условий.
Рекомендуемая
литература 61,
64, 69.
Б В
