5 Функции Уолша и их свойства

Полными ортогональными системами базисных кусочно-постоянных функций являются системы функций Уолша и Хаара. Для представления дискретных сигналов используются в основном функции Уолша.

Для нормированных функций Уолша принято обозначение wal(n,θ), где n - номер функции, а θнаходится в интервале 0≤θ<1. Обычно рассматривается множество функций Уолша wal(n,θ) при n=0,1,...,N-1, где N=2i и i=1,2,3,...

Чаще всего используются функции Уолша, которые на отрезке своего существования принимают лишь значения .

Введём безразмерное время 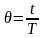, тогда k-ая функция Уолша обозначается символом .

Разложение сигнала в ряд по функциям Уолша на заданном отрезке времени имеет вид:

- коэффициенты ряда.

Графики функций Уолша

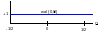
Функции Уолша различают по их порядку и рангу. Под порядком имеют ввиду максимальный из содержащих единицу номеров разрядов при двоичном представлении числа n, рангом называют число единиц в двоичном выражении n. Например, порядок и ранг функции wal(5,θ) равны соответственно 3 и 2, так какдвоичным выражением числа 5 является 101 (имеется ввиду обычное двоичное кодирование чисел; см. второй столбец табл. 3.2). Функции Уолша могут быть представлены в виде произведений функций Радемахера. Номера функций Радемахера, образуюших функции Уолша wal(n,θ) определяются по номерам последних, выраженных в двоичном коде Грея. Для чисел n от 0 до 15 их нумерация кодом Грея дана в последнем столбце табл.3.2. Номера перемножаемых функций Радемахера отвечают номерам разрядов, в которых имеются единицы, закодированного кодом Грея числа n. Разряды отсчитываются, начиная с младшего разряда. Так определяются как произведение функций Радемахера ункции wal(n,θ) для любых n.Код Грея связан следующим образом с обычным двоичным кодом. Если в обычной двоичной системе исчисления число n=ak-1ak-2...a0, то в коде Грея n=bk-1bk-2...b0, где b0=a0⊕a1, b1=a1⊕a2,...,bk-1=ak-1; ⊕- знак суммирования по модулю два(0⊕0=0; 0⊕1=1; 1⊕0=1; 1⊕1=0). Например, n=2 в обычном двоичном коде записывается как 10. Здесь a1=1, a0=0. Следовательно, b0=a0⊕a1=0⊕1=1, b1=a1=1. Сле-довательно, число n=2 представляется как 11.

Функции Уолша могут быть упорядочены по Уолшу. На практике широкоиспользуется также и другие способы упорядочивания функций Уолша. Имеется упорядочивание функций Уолша по Пэли, упорядочивание функций Уолша по Адамару.

6 Итегральное преобразование Фурье. Спектральная плотность сигналов и ее свойства.

Сигналы связи всегда ограничены во времени и поэтому не являются периодическими. Среди непериодических сигналов наибольший интерес представляют одиночные импульсы (ОИ). ОИ можно рассматривать как предельный случай периодической последовательности импульсов (ППИ) длительностью при бесконечно большом периоде их повторения .

Рисунок 6.1 – ППИ и ОИ.

Непериодический сигнал может быть представлен суммой бесконечно большого числа бесконечно близких по частоте колебаний с исчезающе малыми амплитудами. Спектр ОИ является непрерывным и вводится интегралами Фурье:

- (1) - прямое преобразование Фурье. Позволяет аналитически отыскать спектральную функцию по заданной форме сигнала;

- (2) - обратное преобразование Фурье. Позволяет аналитически отыскать форму по заданной спектральной функции сигнала.

Комплексная форма интегрального преобразования фурье (2) дает двустороннее спектральное представление (имеющее отрицательные частоты) непериодического сигнала в виде суммы гармонических колебаний с бесконечно малыми комплексными амплитудами , частоты которых непрерывно заполняют всю ось частот.

- комплексная спектральная плотность сигнала – комплексная функция частоты, одновременно несущая информацию как об амплитуде, так и о фазе элементарных гармоник.

Поскольку для представления спектров непериодических сигналов используются интегральные преобразования Фурье, эти спектры сплошные.

Спектральная плотность может быть представлена в виде:

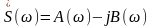
Вещественная часть спектральной плотности есть чётная функция частоты:

Мнимая часть спектральной плотности есть нечётная функция частоты:

Если записать спектральную плотность в показательной форме, то можно выделить её модуль и аргумент:

Модуль спектральной плотности называется амплитудным спектром сигнала:

а аргумент спектральной плотности – фазовым спектром сигнала.

Пара преобразований Фурье имеет фундаментальное значение в теории электросвязи, так как многие характеристики сигналов связаны между собой этими преобразованиями.

Все свойства спектральной плотности объединены в основных теоремах о спектрах.

Преобразуем формулу (2):

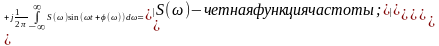
Тригонометрическая форма интегрального преобразования фурье дает одностороннее спектральное представление (не имеющее отрицательных частот) непериодического сигнала:

.