33Критерии качества оптимального приёмника
I.Критерий идеального наблюдателя, или критерий Котельникова
Это критерий, по которому качество приёмника оценивают безусловной вероятностью правильного приёма сигнала.
Пусть
на вход приёмника в течение тактового
интервала 0-Т приходит некоторый элемент
сигнала Z(t).
Предположим, что приёмник принимает
при этом решение, что передан символ
.
Вероятность того, это решение правильно,
очевидно, равна условной вероятности
того, что действительно передавался
символ
при условии прихода реализации элемента
сигнала Z(t),
.
Её называют обычно апостериорной
вероятностью символа
(то есть вероятностью, определённой
после опыта, заключающегося в наблюдении
и анализе сигнала Z(t).)
Очевидно, что вероятность правильного приёма будет максимальной в такой решающей схеме, для которой апостериорная вероятность максимальна. Другими словами, критерий идеального наблюдателя обеспечивается решающей схемой, построенной по правилу максимума апостериорной вероятности – решение о принимается в том случае, если выполняется система из m-1 неравенств:
(3.3)
Согласно известной формуле Бейеса для :
(3.4)
где
– n-мерная
плотность вероятности вектора Z,
– априорная вероятность передачи
символа
(то есть та вероятность, которая имеет
место до наблюдения и анализа, определяемая
статистикой источника сообщения и
правилом кодирования).
Подставив (3.4) в (3.3) и учитывая, что – безусловная плотность вероятности, не являющаяся функцией i, можно записать правила решения для идеального наблюдателя в следующей форме:
(3.5)
где
– функция правдоподобия i-той
гипотезы
Для
построения решающей схемы по правилу
(3.5) необходимо знать априорные вероятности
символов
,
определяемые источником, а также
свойства модулятора и канала, определяющие
условные плотности вероятности.
– функции правдоподобия.
Недостатком критерия максимума апостериорной вероятности является тот факт, что он обеспечивает большую вероятность правильного приёма за счёт сокращения области маловероятных и расширения области приёма высоковероятных символов; в результате редко передаваемые символы передавались бы менее надёжно, а они несут больше информации.
II.
Правило (3.5) можно записать иначе-
решение о том, что передавался символ
,
должно приниматься, если для всех
выполняется m-1
неравенств:
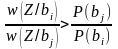(3.6)
Отношение
в левой части этого неравенства
называется отношением правдоподобия
двух гипотез о том, что передавался
символ
.
Его обозначают
.
Для двоичной системы правило сводится к проверке
(3.7)
Во многих случаях различные ошибки приводят к различным последствиям.
III.
Учёт последствий ошибок различного
рода (связанных с передачей различных
символов приводит к обобщению критерия
идеального наблюдателя, известного
под названием критерия минимального
среднего риска (или байесовского
критерия). Если при передаче символа
принят символ
,
то при
имеет место ошибка.
Чтобы учесть неравноценность различных ошибок, будем с каждой парой символов и связывать некоторую численную величину, называемую «потерей», обозначив её Lij. Величина «потери» зависит от того какой символ принят вместо переданного . Правильному приёму при этом приписывается нулевая потеря.
Так как при передаче символа символ появляется с определёнными вероятностями как реализации некоторой дискретной случайной величины, можно говорить об условном математическом ожидании величины «потери» при передаче конкретного символа . Назовём это условное математическое ожидание условным риском:
Интервал
берётся по области
решающей схемы и представляет вероятность
того, что сигнал Z(t)
попал в эту область, если передавался
символ
.
Усреднив условный риск
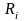по всем символам
,
получим величину, называемую средним
риском:
Критерий
минимального среднего риска заключается
в том, что оптимальной считается решающая
схема, обеспечивающая наименьшее
значение среднего риска
.
Приёмник, работающий по такому критерию
называется байесовским. Из (3.9) видно,
что при использовании этого критерия
нужно помимо априорных вероятностей
передачи отдельных символов знать и
величины потерь Lij.
Заметим, что если считать все ошибки
равноценными (
),
то критерий минимального среднего
риска совпадает с критерием идеального
наблюдателя, а байесовский приёмник
совпадает с идеальным приёмником
Котельникова.
IV Ситуация, в которой практически невозможно определить априорную вероятность передачи отдельных элементарных сообщений, а последствия ошибок разного рода неодинаковы, особенно типична для радиолокации, когда приёмник, анализируя принимаемое колебание Z(t) (отражённый сигнал плюс помеха), должен определить, имеется в данном направлении и на данном расстоянии объект наблюдения (цель) или нет. Последствия двух родов ошибок ложной тревоги и пропуска цели – неравноценны.
В
этой и других сходных ситуациях чаще
всего пользуются критерием приёма,
известным под названием критерия
Неймана Пирсона. Суть его заключается
в том, что решающая схема считается
оптимальной, если при заданной вероятности
ложной тревоги
обеспечивается минимальная вероятность
пропуска цели
.Введём
в рассмотрение функции правдоподобия
гипотезы об отсутствии цели w(Z/0)
и о наличии цели w(Z/1).
Минимизация при заданной величине достигается, если решение о наличии цели принимается при выполнении неравенства.
Где
–
пороговый уровень, определяемый заданной
вероятностью ложной тревоги
В
технике связи преимущественно применяют
правило максимального правдоподобия.
В том случае, когда все символы передаются
равновероятно, правило максимального
правдоподобия переходит в критерий
идеального наблюдателя. Часто это
правило решения применяют и при
неизвестных или известных но не
одинаковых априорных вероятностях
символов. Правило максимального
правдоподобия переходит в критерий
минимума среднего риска, если
положить
Существуют
так же и другие критерии, например,
критерий взвешенной вероятности ошибки,
минимаксный критерий, при котором
коэффициент потерь считается заданным
и другие.
Выбор того или иного варианта критерия оптимальности называют стратегией. Стратегия определяется исходными данными при проектировании. Наиболее простая стратегия соответствует критерию максимального правдоподобия. Рассматриваемые задачи в статистической теории связи классифицируются как задачи распознавания и задачи обнаружения сигнала. Например, при амплитудной телеграфии (АТ) – передача с «пассивной паузой» - приёмное устройство выполняет функции обнаружителя. (Термин «обнаружение» первоначально возник в радиолокации). В случае частотной или фазовой телеграфии (ЧТ или ФТ) приёмное устройство работает по принципу распознавания.