24 Воздействие случайных сигналов на линейные стационарные цепи

Пусть четырехполюсник является линейным и на его вход подан стационарный случайный процесс с нулевым средним значением. Спектральная плотность этого процесса на входе равна G₁(ω), акорреляционная функция — B₁(τ). Коэффициент передачи четырехполюсника равен K(jω).

Требуется найти корреляционную функцию Β₂(τ) и соответствующую ей спектральную плотность мощности случайного процесса G₂(ω) на выходе четырехполюсника.

Если на вход подан стационарный случайный процесс с нулевым средним значением, то на выходе установившийся процесс также будет стационарным.

Можно показать, что спектральная плотность мощности входного стационарного случайного процесса определяется также, как и спектральная плотность мощности детерминированного сигнала, т.е.

(5.17)где 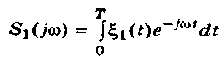— спектральная плотность отрезка входного стационарного случайного процесса ξ₁(t) в интервале 0-Т.

Спектральная плотность мощности выходного случайного стационарного процесса

так как спектральная плотность отрезка выходной стационарной случайной функции равна

S₂(jω) = Si(jω)K(jω).

Корреляционная функция случайного процесса на выходе линейного четырехполюсника

Если линейный четырехполюсник задан импульсной характеристикой h(t), то его реакция на входной случайный процесс ξ₁(t) может быть вычислена с помощью интеграла Дюамеля

Полагаем, что входной случайный процесс является стационарным. В этом случае при вычислении среднего значения и корреляционной функции можно воспользоваться формулами (4.17), (4.19). Среднее значение

Как следует из (5.21), (5.22), при преобразовании линейным четырехполюсником случайного стационарного процесса он становится нестационарным.

Признаками нестационарности являются: а) зависимость среднего значения от времени; б) зависимость корреляционной функции не от разности t₂ - t₁,а от моментов времени t₂ и t₁.

Отметим следующие особенности, связанные с прохождением случайных сигналов и помех через линейные системы.

1. Если входной случайный процессξ(t)подчиняется нормальному закону, распределения, то и выходной случайный процесс ξ₂(t) также подчиняется нормальному закону.

2. Случайный процесс ξ₁(t), подчиняющийся любому закону распределения, при прохождении через линейный четырехполюсник нормализуется, причем закон распределения случайного процесса ξ₂(t), тем ближе к нормальному закону, чем уже полоса пропускания этого четырехполюсника.

25 Воздействие стационарных случайных сигналов на безынерционные нелинейные цепи

Задача формулируется следующим образом. Для данной функции распределения w(x₁,x₂,...,x_n; t₁,t₂,...,t_n) случайной величины ξ₁(t) на входе и заданном операторе нелинейного преобразования у = f(x), найти функцию распределения случайной величины ξ₂(t) на выходе нелинейного звена системы.

Если функция распределения w(y₁,y₂,…,y_n ; t₁,...,t_n) будет найдена, то по ней нетрудно найти всевозможные статистические характеристики (моменты п-го порядка).

Задача более наглядна и понятна для одномерного случая, когда нелинейный оператор представлен только одним уравнением у = f(x), a плотность распределения вероятности входного случайного процесса ξ₁(t) равна w(x).

Пусть существует обратная функция x= φ(у). В этом случае, если случайная величина ξ₁находится в пределах x₀<ξ₁≤ x₀ + dx, то случайная величина ξ₂ будет находиться в пределах у₀<ξ₂≤ у₀ + dy(рис.5.8). Вероятность этих событий равны. Поэтому будут равны и заштрихованные площади:

w(x)dx = w(y)dy.

Из полученного равенства находим

Если известны оператор у = f(x) и двумерная плотность распределения вероятности входного случайного процесса w(x₁,x₂;t₁,t₂), то статистические характеристики случайного процесса (среднее значение и корреляционная функция) определяются по формулам, приведенным ниже.

Среднее значение

Корреляционная функция