Система уравнений (дифференциальная и слабая формы), описывающая движение упругопластического тела.
Поскольку равновесие сил в системе не зависит от того, обратимы или необратимы деформации, уравнения движения (равновесия), как и кинематические связи, для упругого и упругопластического материала имеют одинаковый вид:
,
(5.139)
,
(5.140)
,
(5.141)
.
(5.142)
Слабая форма уравнений движения (равновесия) – принцип возможных перемещений – выглядит также одинаково:
(5.143)
где
– вариация поля перемещений, то есть
поле таких достаточно гладких функций,
что
на
.
Система (5.139), (5.140) и уравнение (5.143) эквивалентны для достаточно гладких полей перемещений и напряжений.
Докажем сначала, что из (5.143) следует (5.139), (5.140).
.
(5.144)
По формуле Гаусса–Остроградского, учитывая, что на , получаем
.
(5.145)
Подставляя (5.144) и (5.145) в (5.143), получаем (5.139), (5.140).
Теперь покажем, что из (5.139), (5.140) следует (5.143).
Умножив (5.139) на
и проинтегрировав по
,
получаем
.
(5.146)
Использовав (5.144) и (5.145), из (5.146) можно легко получить (5.143).
Основное отличие слабой формы от исходной заключается в возможности находить разрывные решения уравнений движения.
Для получения полной системы уравнений упругопластичности к уравнениям движения и кинематическим связям добавим определяющие соотношения материала:
1. для теории упругости
(5.147)
2. для теории пластичности
(5.148)
Полная система статических уравнений линейной теории упругости имеет вид
,
(5.149)
Функция
положительно определена. Решение задачи
статического упругого нагружения
состоит в нахождении полей перемещений,
деформаций и напряжений, удовлетворяющих
этим уравнениям.
Система уравнений в скоростях (дифференциальная и вариационная формулировки), описывающая квазистатическое деформирование упругопластического тела.
Уравнения (5.149) непригодны для описания квазистатического деформирования упругопластической среды, так как не отображают изменения внешних сил. Поэтому полная система уравнений квазистатического деформирования упругопластических тел формулируется в скоростях:
,
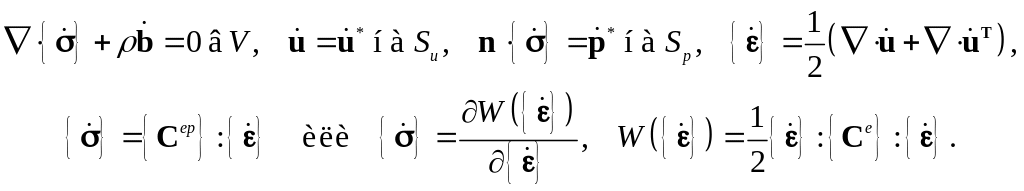(5.150)
Функция
неотрицательная. Решить уравнения
(5.150) – значит для известных полей
перемещений, деформаций и напряжений
(входят в
)
найти поля скоростей перемещений
,
деформаций
и напряжений
,
удовлетворяющих уравнениям (5.150).
Вместо исходных дифференциальных уравнений или их слабой формы можно использовать вариационные принципы.
Для упругого деформирования – принцип минимума потенциальной энергии. Введем функционал, определяющий полную потенциальную энергию.
,
(5.151)
где
– кинематически возможное (допустимое)
поле перемещений, то есть поле,
удовлетворяющее условию
на
.
Перепишем уравнения равновесия и
граничные условия для напряжений в
следующем виде:
(5.152)
Система (5.152) представляет собой систему уравнений Эйлера и естественных граничных условий вариационного уравнения
,
на
.
(5.153)
Наоборот, среди всех кинематически
возможных полей перемещений действительное
поле перемещений
(удовлетворяющее (5.152)) доставляет полной
потенциальной энергии абсолютный
минимум, равный
.
(5.154)
.
(5.155)
Обозначим
.
Тогда
,
как было установлено ранее (см. (5.144)).
Учитывая это и пользуясь формулой
Гаусса– Остроградского (см. (5.145)), из
(5.155) получим
.
(5.156)
Поскольку это выполняется для произвольного
,
из
следует выполнение (5.152).
Покажем теперь следствие из выполнения (5.152). Начнем с доказательства справедливости (5.154).
.
(5.157)
,
(5.158)
где
из уравнений равновесия.
(5.159)
Подставляя (5.159) в (5.157), получим (5.154).
Представим кинематически возможное
поле перемещений
в виде
,
,
так как
,
.
Тогда (5.151) приобретает вид
.
(5.160)
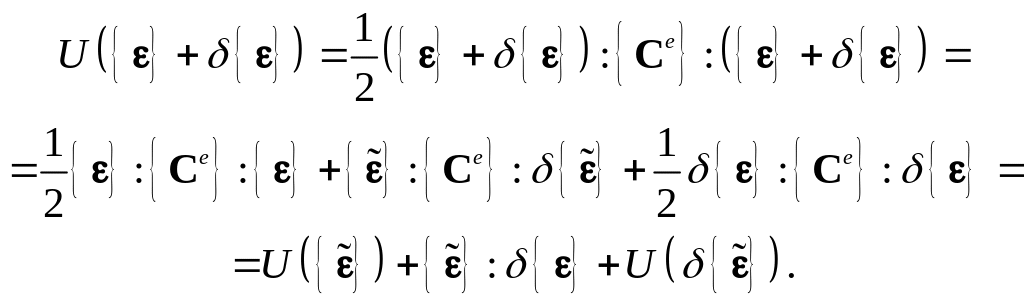(5.161)
Из (5.160) и (5.161) получаем
(5.162)
Вариация функционала берется на истинном
поле
.
Поскольку
,
то
.
(5.163)
То есть истинное решение доставляет
стационарное значение функционалу
.
Покажем, что это стационарное значение
– абсолютный минимум.
.
(5.164)
В функционале, в отличие от исходных уравнений, не требуется гладкости напряжений.
Рассмотрим теперь упругопластический материал. Введем функционал
.
(5.164)
Здесь
– кинематически возможное поле скоростей
перемещений, то есть скоростей перемещений,
удовлетворяющих условию
.
Рассмотрим уравнения равновесия и
граничные условия в скоростях
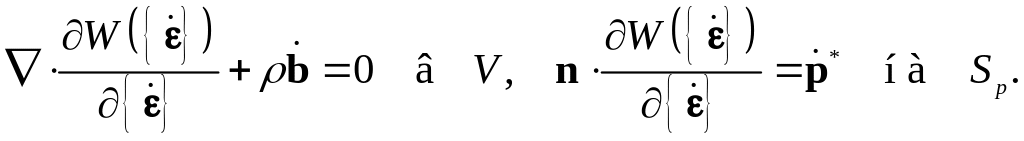(5.165)
Вариационный принцип для достаточно гладких полей скоростей деформаций состоит в том, что система (5.165) является системой уравнений Эйлера и естественных граничных условий вариационного уравнения
.
(5.166)
Наоборот, среди всех кинематически возможных полей скоростей перемещений действительное поле скоростей перемещений доставляет функционалу (5.164) для упрочняющегося тела абсолютный минимум. а для идеального упругопластического тела – минимум, равный
.
(5.167)
Доказательство аналогично случаю
линейной теории упругости с заменой
и
,
кроме последнего равенства, когда для
идеального упругопластического материала
,
может достигаться
при
.
Если для идеального упругопластического
материала при решении конкретной задачи
обеспечивается условие
при
для всех кинематически возможных полей
скоростей во всех точках тела, то и для
идеального упругопластического материала
достигается абсолютный минимум, так
как при
справедливо равенство
.
(5.168)
Выполнение этого условия обеспечивается,
если для данного распределения напряжений
и деформаций
и
невозможно деформирование без появления
скоростей упругих деформаций для всех
кинематически возможных полей скоростей
во всех точках тела
.