
- •Глава 5. Упругопластическое деформирование твердого тела
- •Идеальные модели упругопластического статического растяжения. Изотропное и кинематическое упрочнение. Условия пластичности Треска, Мизеса, Кулона – Мора, Друкера – Прагера.
- •5.1.3. Кривая текучести.
- •5.1.4. Критерии текучести Треска и Мизеса на девиаторной плоскости.
- •Поведение поверхности нагружения при изотропном, кинематическом и комбинированном упрочнениях. Закон пластического упрочнения.
- •Принцип максимума Мизеса и его следствия. Постулат Друккера и его следствия.
- •Определяющие соотношения упругопластического материала с гладкой поверхностью текучести. Уравнения Прандтля – Рейсса для идеального упругопластического материала.
- •Принцип макродетерменизма Клюшникова и его следствие (необходимость потенциальной формы записи определяющих соотношений пластичности в скоростях).
- •Система уравнений (дифференциальная и слабая формы), описывающая движение упругопластического тела.
- •Система уравнений в скоростях (дифференциальная и вариационная формулировки), описывающая квазистатическое деформирование упругопластического тела.
- •Теорема единственности решений квазистатических задач упругопластического деформирования.
Определяющие соотношения упругопластического материала с гладкой поверхностью текучести. Уравнения Прандтля – Рейсса для идеального упругопластического материала.
Пусть скорости деформаций удовлетворяют выражению
![]() (5.33)
(5.33)
и в упругой области выполняются соотношения
![]() или
или
![]() ,
(5.34)
,
(5.34)
а в пластической имеется ассоциированный закон течения
![]() .
(5.35)
.
(5.35)
Если материал с упрочнением, то
 (5.36)
(5.36)
Для идеального упругопластического материала
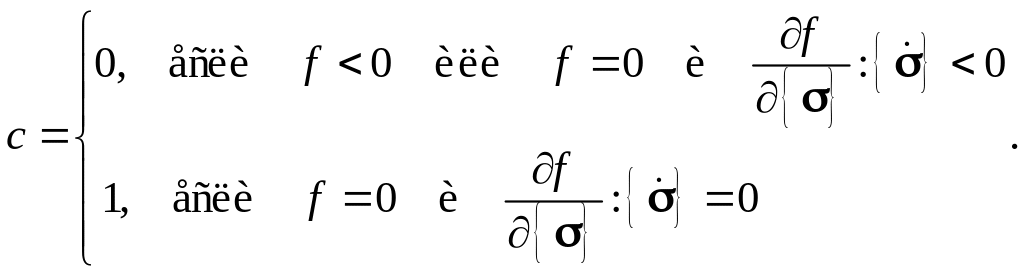 (5.37)
(5.37)
Найдем
для упрочняющегося материала. Для начала
введем параметр упрочнения
![]() (рис. 5.1.8):
(рис. 5.1.8):
 .
(5.38)
.
(5.38)
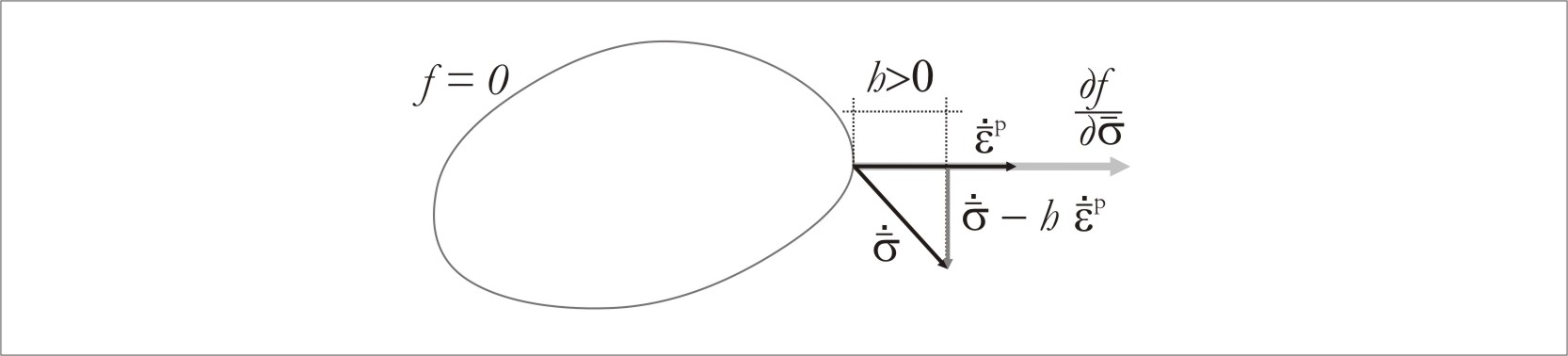
Рис. 5.1.8. Параметр упрочнения.
Тогда
![]() .
(5.39)
.
(5.39)
Рассмотрим случай пластического
деформирования
![]() .
Подставив (5.39) в (5.35), получим
.
Подставив (5.39) в (5.35), получим
 .
(5.40)
.
(5.40)
Пусть тензор
![]() в девятимерном пространстве представляется
вектором единичной нормали к поверхности
текучести.
в девятимерном пространстве представляется
вектором единичной нормали к поверхности
текучести.
![]() .
(5.41)
.
(5.41)
Подставляя (5.41) в (5.35), получим
![]() .
(5.42)
.
(5.42)
Перепишем (5.36) в виде
 (5.43)
(5.43)
Из (5.33) и (5.34) следует, что
![]() .
(5.44)
.
(5.44)
Подставляя (5.42) в (5.44) и помня, что , получим
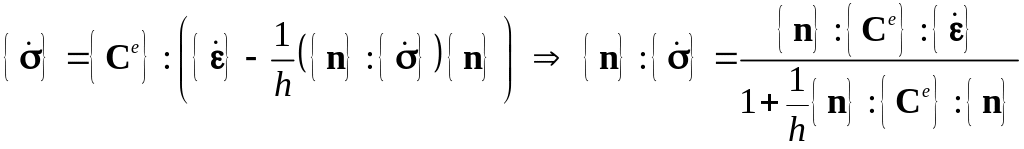 .
(5.45)
.
(5.45)
Из (5.41) и (5.45) получаем
 .
(5.46)
.
(5.46)
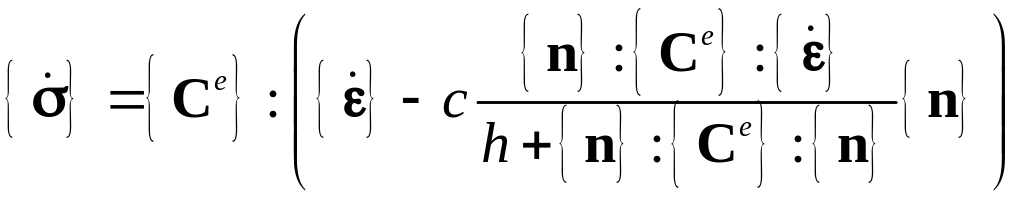 .
(5.47)
.
(5.47)
Так как
и
![]() (по свойству положительной определенности
тензора упругих определяющих соотношений),
(5.43) можно с учетом (5.45) переписать в виде
(по свойству положительной определенности
тензора упругих определяющих соотношений),
(5.43) можно с учетом (5.45) переписать в виде
 (5.48)
(5.48)
Теперь найдем для идеального упругопластического материала.
Перепишем (5.35), (5.37) с учетом (5.41):
![]() .
(5.49)
.
(5.49)
 (5.50)
(5.50)
Из (5.44) и (5.49) при следует
![]() .
(5.51)
.
(5.51)
Поскольку
,
когда
![]() ,
из (5.51) получаем
,
из (5.51) получаем
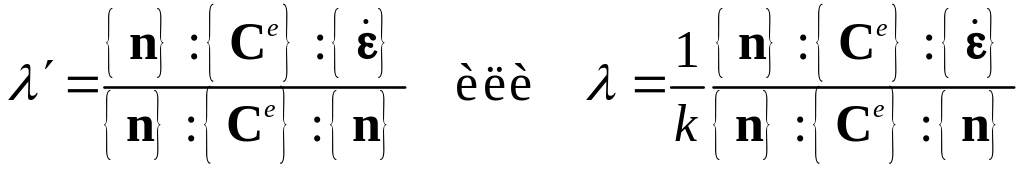 .
(5.52)
.
(5.52)
Подставляя (5.52) в (5.51), имеем
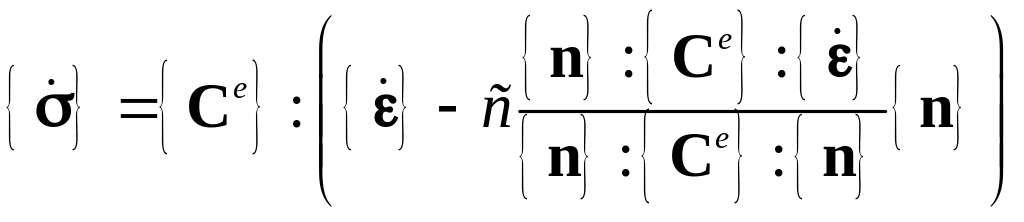 .
(5.53)
.
(5.53)
Так как для пластического течения
![]() ,
то условие (5.50) можно переписать в виде
(5.48). Действительно, при
,
то условие (5.50) можно переписать в виде
(5.48). Действительно, при
![]() может быть только упругое деформирование,
так как из (5.52) следует невозможность
выполнения неравенства
может быть только упругое деформирование,
так как из (5.52) следует невозможность
выполнения неравенства
![]() при пластической деформации (так как
).
Покажем, что неравенство
обязательно соответствует пластической
деформации. Пусть при
при пластической деформации (так как
).
Покажем, что неравенство
обязательно соответствует пластической
деформации. Пусть при
![]() и
происходит упругое деформирование.
Тогда
и
происходит упругое деформирование.
Тогда
![]() ,
а значит
,
а значит
![]() ,
что противоречит тому, что для идеального
упругопластического тела при упругом
деформировании
и
,
что противоречит тому, что для идеального
упругопластического тела при упругом
деформировании
и
![]() .
.
Формулы (5.47) и (5.53) можно объединить, так что для идеального упругопластического материала определяющие соотношения будут имеет вид
 ,
(5.54)
,
(5.54)
где
![]() ,
а
определяется соотношениями (5.48). Перепишем
(5.54) в новой форме, введя новую операцию
– тензорное произведение – таким
образом:
,
а
определяется соотношениями (5.48). Перепишем
(5.54) в новой форме, введя новую операцию
– тензорное произведение – таким
образом:
![]() .
.
![]() ,
(5.55)
,
(5.55)
откуда получаем
![]() .
(5.56)
.
(5.56)
![]() .
(5.57)
.
(5.57)
Таким образом, у нас есть единые
определяющие соотношения для
упругопластического материала. Определяя
функцию текучести
![]() ,
получаем различные теории пластического
течения с ассоциированным законом
пластичности.
,
получаем различные теории пластического
течения с ассоциированным законом
пластичности.
Покажем, что если
![]() ,
то материал пластически несжимаем, то
есть
,
то материал пластически несжимаем, то
есть
![]() или
или
![]() (
(![]() – относительное изменение объема).
Имеем
– относительное изменение объема).
Имеем
![]() .
(5.58)
.
(5.58)
![]() .
(5.59)
.
(5.59)
 ,
(5.60)
,
(5.60)
откуда следует
![]() ,
(5.61)
,
(5.61)
аналогично
![]() .
(5.62)
.
(5.62)
Тогда
 ,
(5.63)
,
(5.63)
что и требовалось доказать.
Если поверхность текучести имеет угловые точки (например поверхность Треска), можно либо заменить ее на близкую к ней гладкую поверхность (Треска на Мизеса), либо представить закон пластического течения в виде линейной комбинации вида
![]() .
.
Рассмотрим теорию течения с изотропным упрочнением.
![]() (5.64)
(5.64)
Найдем градиенты
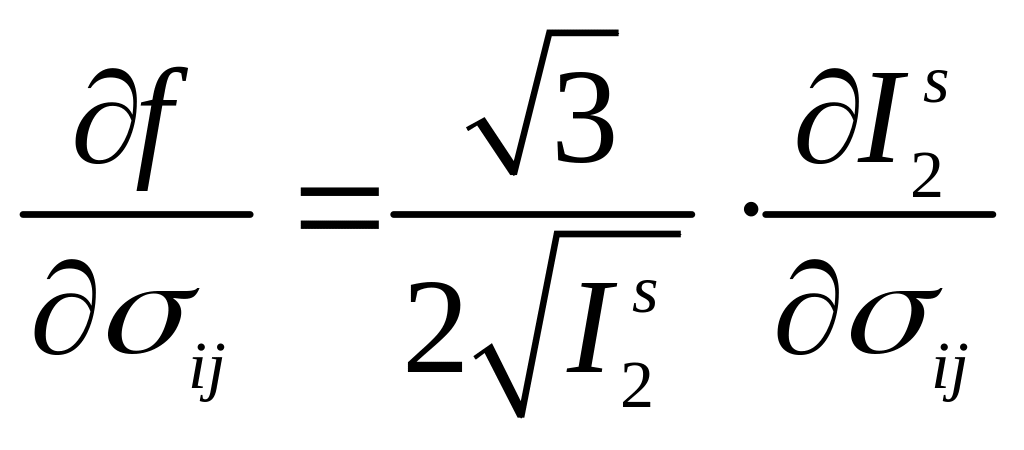 .
.
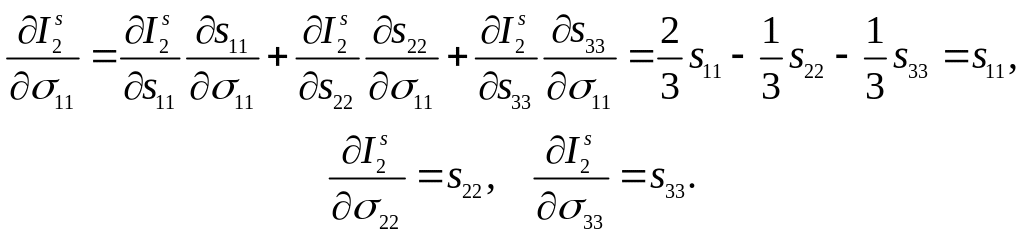 .
(5.65)
.
(5.65)
![]() (5.66)
(5.66)
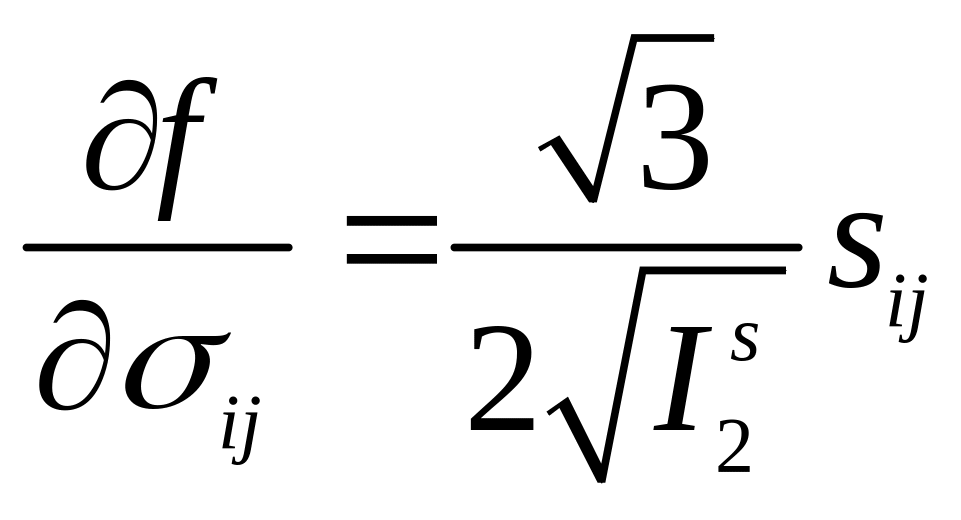 .
(5.67)
.
(5.67)
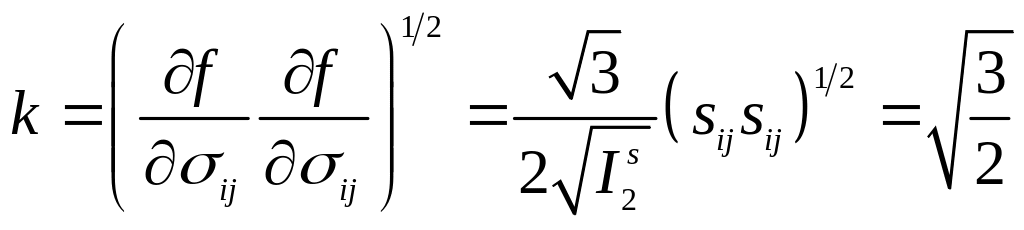 .
(5.68)
.
(5.68)
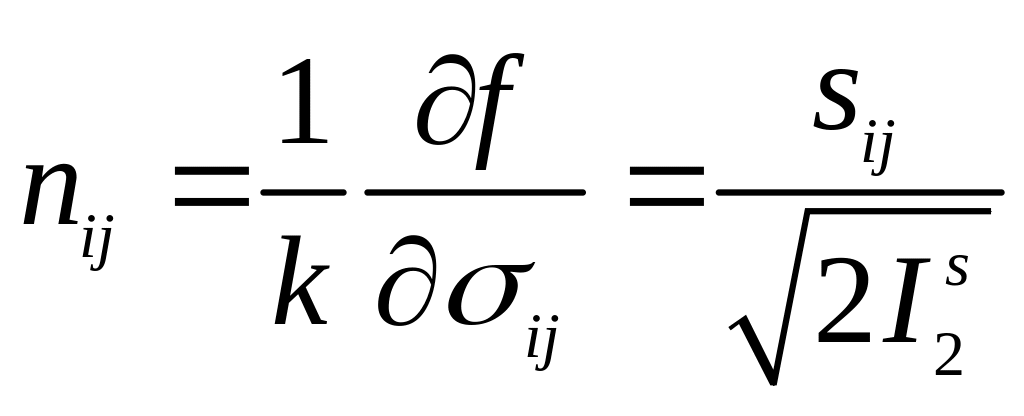 или
или
 .
(5.69)
.
(5.69)
Запишем теперь уравнения теории упругости в следующем виде:
![]() ,
(5.70)
,
(5.70)
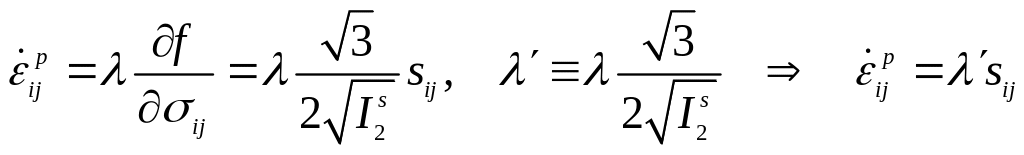 .
(5.71)
.
(5.71)
Дифференцируя уравнения по
![]() ,
получаем уравнения Прандтля–Рейса
для идеально пластического материала.
,
получаем уравнения Прандтля–Рейса
для идеально пластического материала.
![]() (5.72)
(5.72)
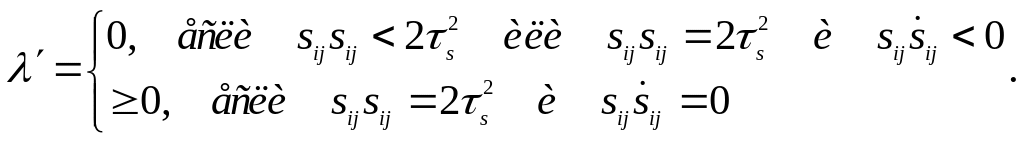 (5.73)
(5.73)
Определим, как должен выглядеть тензор
![]() .
.
Из закона Гука имеем
![]() .
(5.74)
.
(5.74)
В скоростях закон Гука имеет вид
![]() .
(5.75)
.
(5.75)
Тогда
![]() ,
(5.76)
,
(5.76)
так как пропорционально девиаторам.
![]() .
(5.77)
.
(5.77)
Таким образом, для общего выражения (5.54)
имеем
![]() (5.78)
(5.78)
или
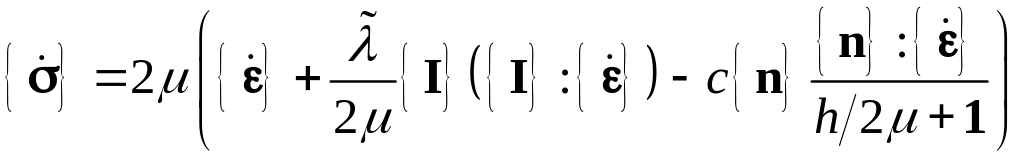 ,
,
или

или
![]() (5.79)
(5.79)
или
![]() .
(5.80)
.
(5.80)
В покомпонентной записи это выглядит следующим образом:
 .
(5.81)
.
(5.81)
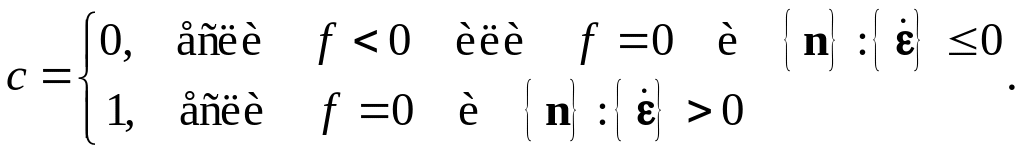 (5.82)
(5.82)
Возможен и другой вариант записи.
Отметим, что знак
![]() совпадает со знаком
совпадает со знаком
![]() так как
так как
![]() .
(5.83)
.
(5.83)
Для упрочняющихся материалов
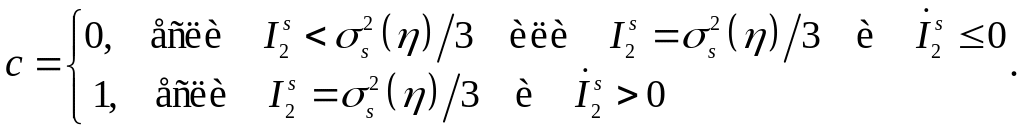 (5.84)
(5.84)
Для идеального упругопластического материала
 (5.85)
(5.85)
Теперь определим параметр
![]() для упрочняющегося материала. Отметим,
что для этой теории пластичности
зависимость параметра
можно заменить на зависимость
для упрочняющегося материала. Отметим,
что для этой теории пластичности
зависимость параметра
можно заменить на зависимость
![]() ,
так как из условия пластичности
,
так как из условия пластичности
![]() .
(5.86)
.
(5.86)
Параметр
![]() можно определить из диаграммы растяжения,
по которой мы можем определить модуль
Юнга
и тангенциальный модуль
(для определения последнего нелинейный
участок диаграммы, соответствующий
деформационному упрочнению, приблизим
некоторым линейным участком). Вспомним,
что
можно определить из диаграммы растяжения,
по которой мы можем определить модуль
Юнга
и тангенциальный модуль
(для определения последнего нелинейный
участок диаграммы, соответствующий
деформационному упрочнению, приблизим
некоторым линейным участком). Вспомним,
что
![]() (5.87)
(5.87)
Для одноосного растяжения или сжатия
![]() ,
остальные
,
остальные
![]() .
Тогда
.
Тогда
![]() ,
(5.88)
,
(5.88)
![]() ,
(5.89)
,
(5.89)
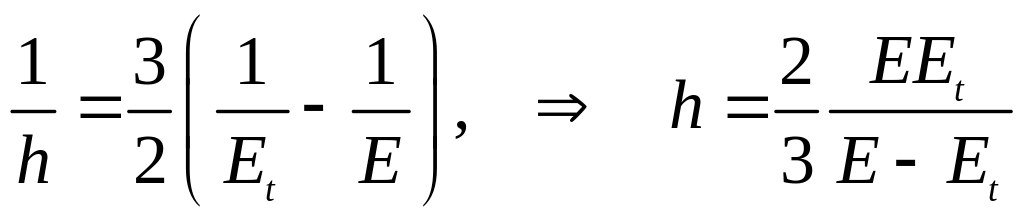 .
(5.90)
.
(5.90)
Теперь рассмотрим теорию течения с кинематическим (линейным) упрочнением.
![]() (5.91)
(5.91)
Отличие от изотропного случая состоит
в замене
на
![]() .
.
Найдем градиенты
 .
.
 .
(5.92)
.
(5.92)
![]() (5.93)
(5.93)
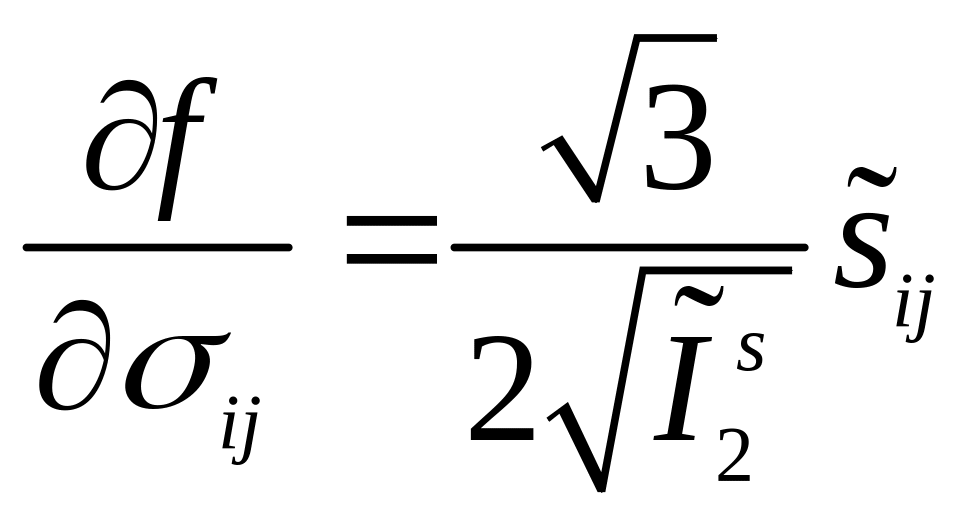 .
(5.94)
.
(5.94)
Аналогично теории с изотропным упрочнением
 или
или
![]() .
.
Формулы для определения
![]() ,
,
,
полученные для теории течения с изотропным
упрочнением остаются в том же виде с
той только оговоркой, что параметр
,
,
,
полученные для теории течения с изотропным
упрочнением остаются в том же виде с
той только оговоркой, что параметр
![]() здесь определяется только для материала
с линейным упрочнением.
здесь определяется только для материала
с линейным упрочнением.
![]() ,
так что
,
так что
![]() .
.
Определим тензор
![]() .
При пластическом течении справедливо
.
При пластическом течении справедливо
![]() .
(5.95)
.
(5.95)
 ,
,
![]() .
(5.96)
.
(5.96)
Аналогично получаем
 .
(5.97)
.
(5.97)
Из (5.95) получаем
![]() .
(5.98)
.
(5.98)
Вектору
![]() в девятимерном пространстве можно
давать разные направления, но его
величина определяется из (5.98) так, что
проекция вектора
на вектор нормали совпадает с проекцией
вектора
в девятимерном пространстве можно
давать разные направления, но его
величина определяется из (5.98) так, что
проекция вектора
на вектор нормали совпадает с проекцией
вектора
![]() .
Направление вектора
дается правилами кинематического
упрочнения (
.
Направление вектора
дается правилами кинематического
упрочнения (![]() ).
).
1. По Прагеру
![]() .
.
![]() .
(5.99)
.
(5.99)
2. По Циглеру
![]() .
.
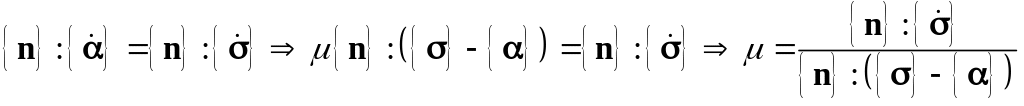 .
(5.100)
.
(5.100)
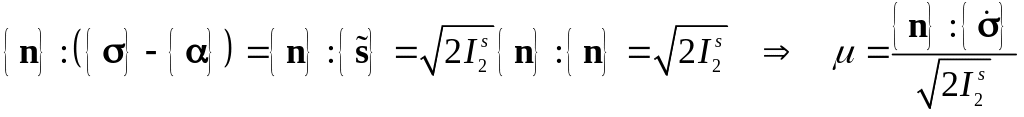 .
(5.101)
.
(5.101)
 .
(5.102)
.
(5.102)
В итоге получаем
1. По Прагеру
 .
.
2. По Циглеру
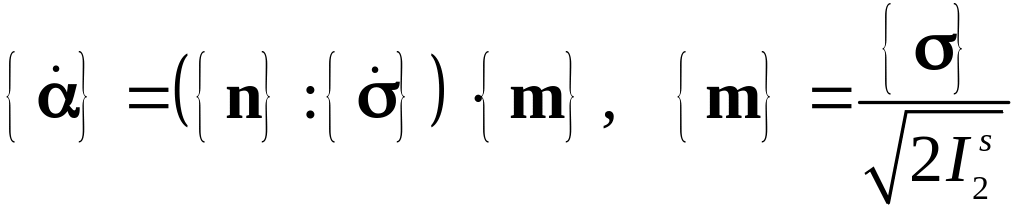 .
.
И, наконец, рассмотрим теорию течения с комбинированным упрочнением.
![]() .
(5.103)
.
(5.103)
 .
(5.104)
.
(5.104)
![]() .
(5.105)
.
(5.105)
Это равенство будет выполнено, если принять, что
![]() ,
(5.106)
,
(5.106)
где
![]() в случае кинематического упрочнения и
в случае кинематического упрочнения и
![]() – в случае изотропного.
– в случае изотропного.
1. По Прагеру
 .
.
2. По Циглеру
 .
.
Определяющие соотношения деформационной теории пластичности. Теорема о простом нагружении. Сопоставление определяющих соотношений деформационной теории пластичности и теории пластического течения.
В теории течения связь между напряжениями и деформациями строится для бесконечно малых величин. Определяющие соотношения записываются либо для бесконечно малых приращений напряжений и деформаций, либо для скоростей. Можно построить и существенно более простые конечные соотношения между напряжениями и деформациями, представляющие собой некоторое обобщение закона Гука. Теория пластичности, основанная на таких определяющих соотношениях, называется деформационной теорией пластичности.
Положим, упругие и пластические деформации связаны с напряжениями следующими соотношениями:
![]() (5.107)
(5.107)
или
![]() .
(5.108)
.
(5.108)
Для упрочняющегося материала
 (5.109)
(5.109)
Для идеального упругопластического материала
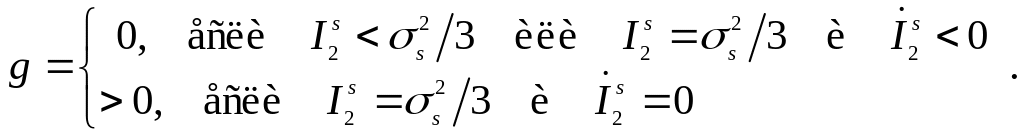 (5.110)
(5.110)
Получим формулы для определения тензора напряжений через тензор деформаций. Подставляя (5.107) в (5.108) получаем
![]() .
(5.111)
.
(5.111)
 ,
(5.112)
,
(5.112)
Получим
![]() для диаграммы одноосного растяжения.
для диаграммы одноосного растяжения.
![]() .
(5.113)
.
(5.113)
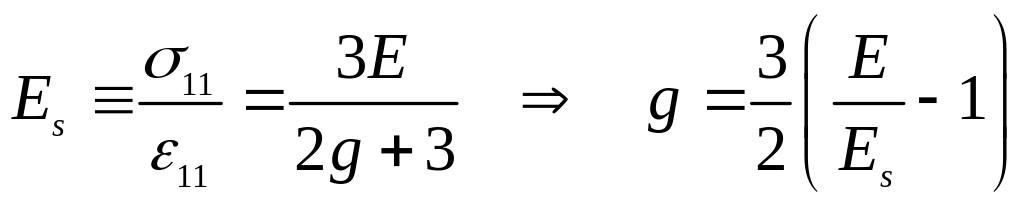 .
(5.114)
.
(5.114)
Более просто получаются соотношения для поиска деформаций через напряжения:
![]() .
(5.115)
.
(5.115)
Произведем сопоставление определяющих соотношений деформационной теории пластичности и теории течения с изотропным упрочнением.
Определим сначала простое (пропорциональное) нагружение, как нагружение, при котором компоненты девиатора тензора напряжений или компоненты тензора напряжений изменяются пропорционально некоторому параметру:
![]() .
.
Примером такого нагружения может служить однородное напряженное состояние (уравнения равновесия и кинематические граничные условия выполняются тождественно), поскольку в этом случае напряженное состояние определяется только внешними силами пропорционально параметру .
Соотношения для пластических деформаций при простом нагружении будут иметь вид
![]() для
теории течения и
для
теории течения и
![]() для деформационной теории.
для деформационной теории.
Теорема. При простом нагружении определяющие соотношения теории течения и деформационной теории эквивалентны.
Доказательство. Пусть осуществляется
простое нагружение. Рассмотрим сперва
случай идеальной пластичности. При
простом нагружении
![]() ,
откуда видим, что
,
откуда видим, что
![]() ,
то есть
,
то есть
![]() ,
,
![]() .
Покажем, что
.
Покажем, что
![]() ,
вычисленные по теории течения и по
деформационной теории совпадают, откуда
и будет следовать эквивалентность
определяющих соотношений.
,
вычисленные по теории течения и по
деформационной теории совпадают, откуда
и будет следовать эквивалентность
определяющих соотношений.
Для теории течения
 ,
(5.116)
,
(5.116)
![]() ,
(5.117)
,
(5.117)
 .
(5.118)
.
(5.118)
Для деформационной теории
![]() .
(5.119)
.
(5.119)
![]() .
(5.120)
.
(5.120)
Таким образом, в случае идеальной пластичности утверждение теоремы доказано. Докажем его для случая упрочнения.
Для теории текучести
 ,
(5.121)
,
(5.121)
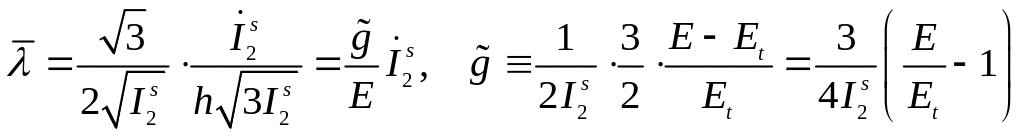 .
(5.122)
.
(5.122)
Найдем для деформационной теории.
![]() .
(5.123)
.
(5.123)
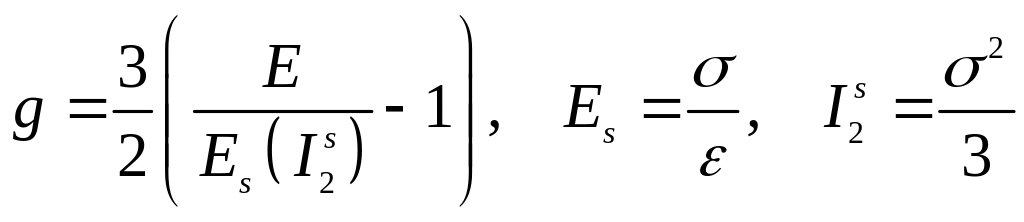 ,
(5.124)
,
(5.124)
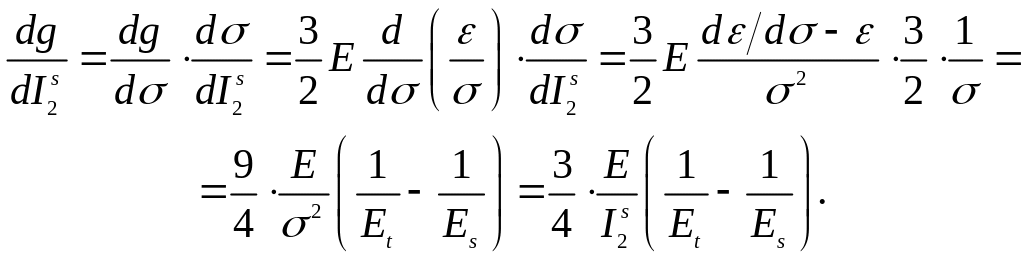 (5.125)
(5.125)
Пусть осуществляется пропорциональное
нагружение. Найдем
![]() по теории течения и по деформационной
теории.
по теории течения и по деформационной
теории.
По теории течения
![]() .
(5.126)
.
(5.126)
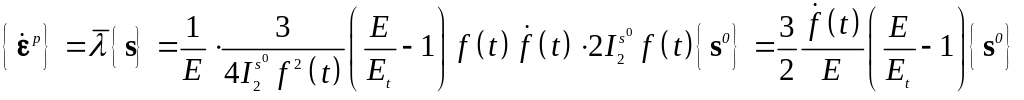 .
(5.127)
.
(5.127)
По деформационной теории
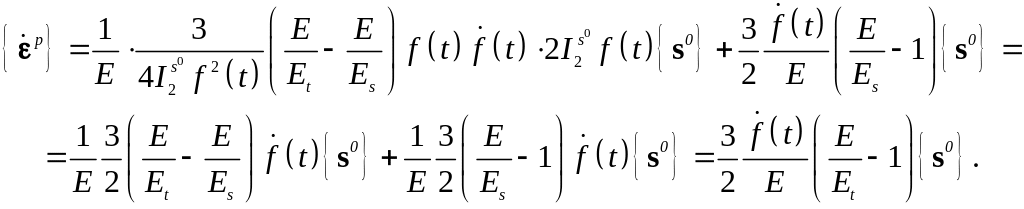 (5.128)
(5.128)
Таким образом,
в деформационной теории и теории течения
совпали, откуда следует, что
![]() также совпали, а значит определяющие
соотношения эквивалентны.
также совпали, а значит определяющие
соотношения эквивалентны.
Доказательство завершено.
Обратная теорема. Если соотношения деформационной теории и теории течения эквивалентны, значит нагружение простое.
Доказательство.
![]() .
(5.129)
.
(5.129)
Интегрируя (5.129), получаем
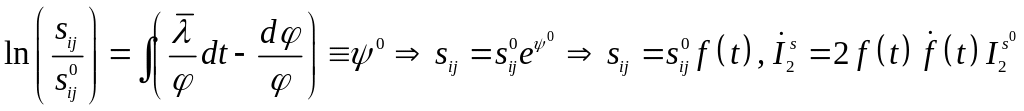 .
(5.130)
.
(5.130)
Поскольку
![]() и
и
![]() ,
то
,
то
![]() ,
что и требовалось доказать.
,
что и требовалось доказать.
Выпишем теперь скорости деформирования для деформационной теории и теории течения соответственно.
Для теории течения имеем
![]() ,
(5.131)
,
(5.131)
для деформационной теории:
![]() .
(5.132)
.
(5.132)
По сравнению с теорией течения деформационная теория имеет два недостатка:
1. не зависит от пути деформирования,
2. из (5.132) видно, что при
![]() (нейтральное нагружение)
(нейтральное нагружение)
![]() терпит разрыв.
терпит разрыв.
Уравнения теории течения задают как непрерывные функции от , являющиеся однородными функциями первой степени, так как
,
Таким образом, по теореме Эйлера об
однородных функциях можно ввести
однородную потенциальную функцию второй
степени
![]() ,
имеющую непрерывные первые производные
и кусочно непрерывные вторые, такую,
что
,
имеющую непрерывные первые производные
и кусочно непрерывные вторые, такую,
что
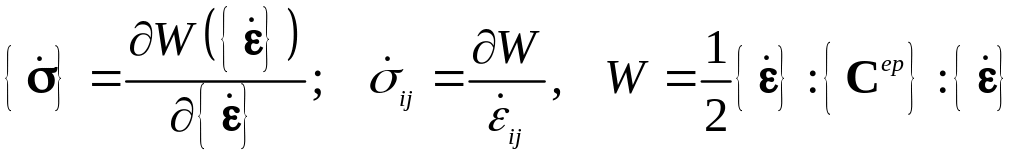 .
(5.133)
.
(5.133)
Уравнения деформационной теории пластичности в этот класс не входят.
