3. Принцип максимума Мизеса и его следствия. Постулат Друккера и его следствия.

Основная гипотеза теории пластичности состоит в том, что тензор деформаций можно представить в виде суммы тензора упругих и тензора пластических деформаций, что справедливо также и для девиаторов

.

Введем понятие мощности внутренних сил на единицу объема:

. (5.26)

Из термодинамических соображений . Эта величина называется мощностью пластической деформации.

Рассмотрим поверхность нагружения или поверхность текучести . при фиксированных значениях и рассмотрим допустимые напряжения , то есть напряжения, удовлетворяющие неравенствам в случае упрочнения или в случае идеальной упругопластичности.

Принцип максимума Мизеса (принцип максимума скорости диссипации механической энергии, постулат максимальной пластической работы) формулируется следующим образом: для истинного поля напряжений мощность пластических деформаций не меньше, чем для любого допустимого полян напряжений , то есть

. (5.27)

Если ввести в девятимерном пространстве векторы напряжений и деформаций

, ,

(компоненты вектора деформаций откладываются по тем же осям. что и компоненты вектора перемещений), можно записать (5.27) в виде

. (5.28)

Из этого неравенства следует:

1. выпуклость (по крайней мере, невогнутость) поверхности нагружения или текучести;

2. для регулярной функции нагружения – нормальность вектора к поверхности нагружения.

Докажем эти следствия, для чего рассмотрим худший вариант, когда находится на поверхности нагружения (если выполнено в этом случае, то выполнено и в остальных).

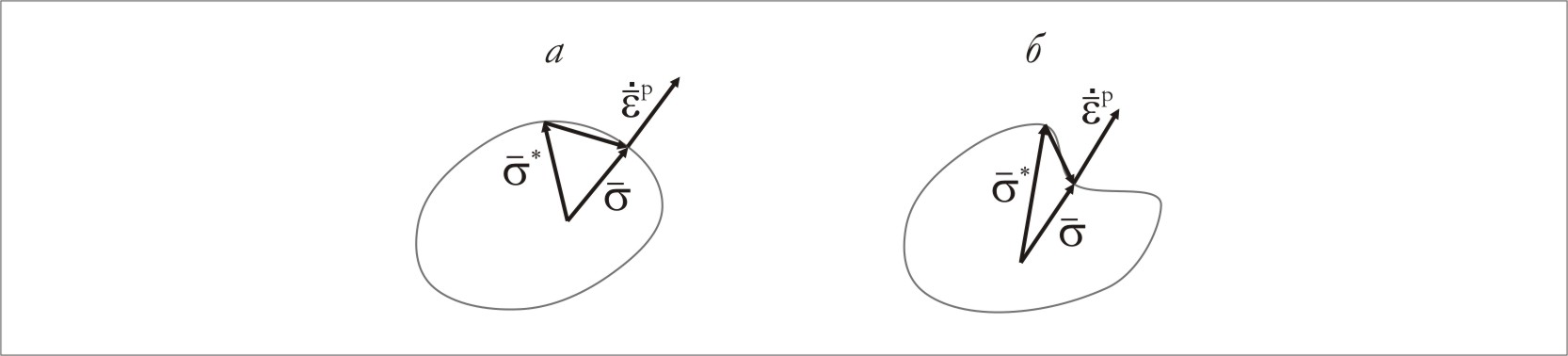
Рис. 5.1.6. Выпуклость поверхности текучести.

Неравенство (5.28) говорит о том, что любой вектор должен составлять нетупой угол с вектором . В случае, если поверхность невогнутая, это возможно только если направлен по нормали к поверхности (рис. 5.1.6. а), что доказывает второе следствие. Если же поверхность вогнута, то всегда найдется такой вектор , который составляет тупой угол с (рис. 5.1.6. б), что доказывает первое следствие.

Второе следствие также можно доказать формально. Пусть функция течения непрерывна и кусочно дифференцируема. Составим локальное условие максимума мощности пластических деформаций как функции от при условии соблюдения условия пластичности =0. Для этого нужно искать условия экстремума функции

, (5.33)

где – неопределенный множитель Лагранжа. Приравнивая нулю производные функции по , получаем так называемый ассоциированный закон течения

. (5.34)

Он показывает, что вектор пластической деформации направлен по нормали к поверхности текукчести.

Альтернативой принципу Мизеса является постулат Друкера, который заключается в следующем: если к телу прикладывается, а затем снимается некоторая нагрузка, тогда 1) работа, производимая дополнительной нагрузкой при нагружении всегда положительна, 2) работа, производимая дополнительной нагрузкой за полный цикл нагружения и разгрузки, как минимум не отрицательна. Дополнительной нагрузкой здесь называется вектор . Постулат Друкера имеет следующую математическую запись:

. (5.29)

Заметим, что для упругопластического тела . Соответственно интеграл разобьется на две части, причем

, (5.30)

поскольку первое слагаемое представляет собой работу упругой деформации по замкнутому пути, а второе равно нулю потому, что упругая деформация однозначно определяется действующим напряжением. Таким образом, из (5.29) следует

. (5.31)

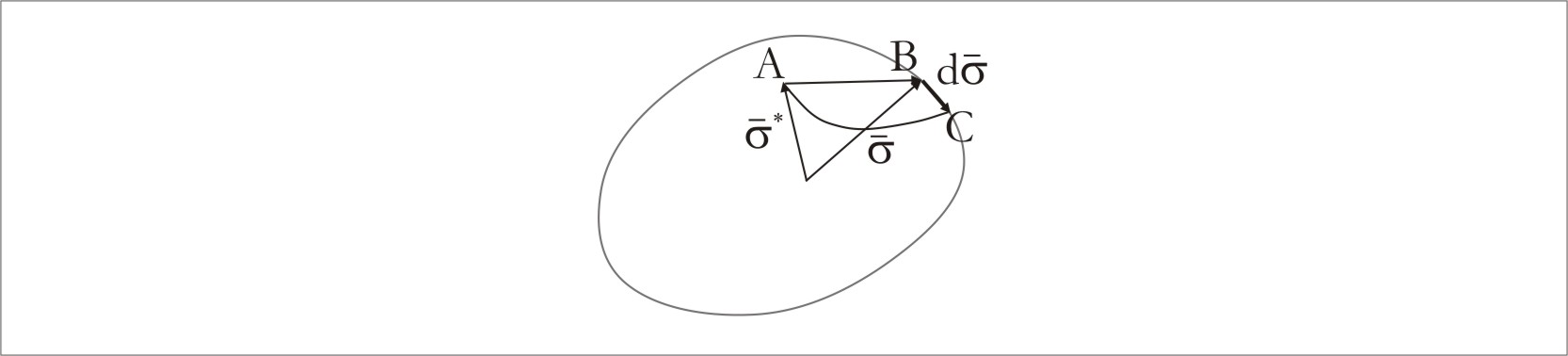
Рис. 5.1.7. Постулат Друкера.

Обходим контур от точки А (от напряжения ), возвращаясь в итоге в эту же точку. На отрезке АВ пластической деформации нет, поэтому это отрезок дает нулевой вклад. На отрезке ВС, лежащем на кривой текучести, напряжение получает приращение , пластическая деформация получает приращение , и работа дополнительного напряжения равна . На участке СА происходи разгрузка, не сопровождающаяся пластической деформацией, так что этот участок тоже дает нулевой вклад.

Таким образом, из (5.29) следует

, (5.32)

что тождественно принципу максимума Мизеса (5.28) с той только разницей, что данное выражение записано не в скоростях, а в приращениях пластической деформации.

Основное отличие принципа Мизеса и постулата Друкера состоит в том, что принцип Мизеса можно сформулировать для любого напряженно-деформированного состояния, а неравенства постулата Друкера выполнены только для однородного НДС.