5.1.4. Критерии текучести Треска и Мизеса на девиаторной плоскости.
В инвариантах девиатора напряжений критерий Треска будет иметь вид
,
(5.11)
а критерий Мизеса
.
(5.12)
Приведенные выше соотношения имеют место для поликристаллических материалов (металлов). Обобщенно пластическое поведение при некоторых нагрузках присуще также и грунтам, однако, рассматривая их, необходимо учитывать внутреннее трение и сцепление между частичками грунта.
Пусть некоторое тело лежит на шероховатой
поверхности,
– сила нормального давления (прижимающая
тело к поверхности и действующая по
нормали к ней), а
– сила, приложенная к телу вдоль
поверхности контакта (рис. 5.1.5. а). Закон
трения Кулона гласит, что при
движение тела относительно поверхности
очень мало, а при
происходит неограниченное скольжение
тела по поверхности (рис. 5.1.5. б).
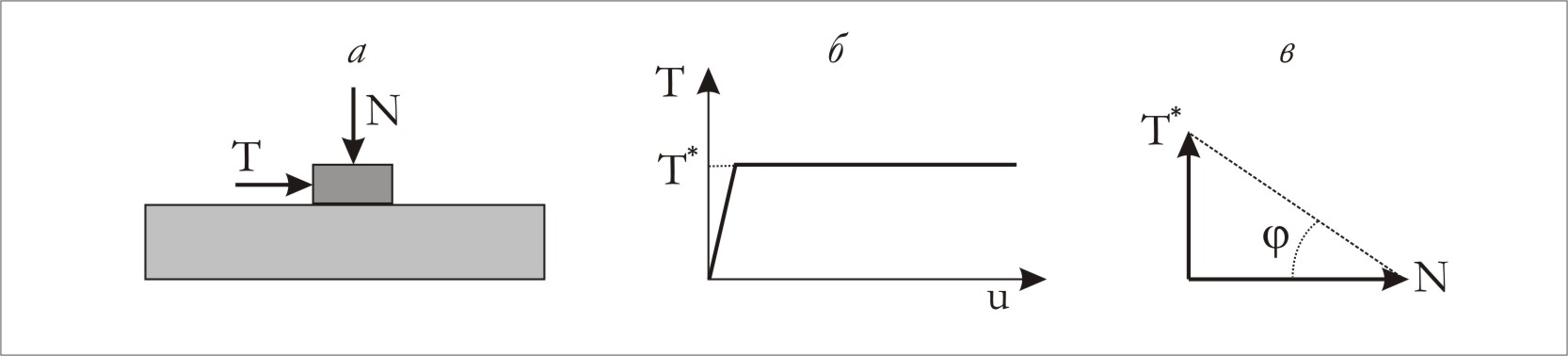
Рис. 5.1.5 Закон Кулона.
Фактически этот закон совпадает с
идеальной упругопластической моделью,
где
– аналог предела текучести, зависящий
от нормальной силы. Эта зависимость
линейна (
– коэффициент трения):
.
(5.13)
Также его можно записать через угол
трения
(рис. 5.1.5. в):
.
(5.14)
Для грунтов существует обобщенный закон
Кулона, в который вводится дополнительный
параметр, являющийся константой материала
– коэффициент сцепления
:
.
(5.15)
Аналог критерия текучести для сыпучей среды, полученный из экспериментальных исследований, выглядит следующим образом:
,
(5.16)
где
– среднее давление.
В общем виде критерии текучести для сыпучих сред и грунтов, представляющие собой обобщение критерия Треска и критерия Мизеса соответственно, выглядят так:
1. критерий Кулона–Мора
;
(5.17)
2. критерий Друкера–Прагера
.
(5.18)
Нетрудно заметить, что при
и
(5.17) превращается в критерий Треска в
виде (5.11), а (5.18) – в критерий Мизеса в
виде (5.12).
Поведение поверхности нагружения при изотропном, кинематическом и комбинированном упрочнениях. Закон пластического упрочнения.
Большинство материалов в обычных условиях при пластическом деформировании упрочняется. В одномерном случае это выражается в увеличении предела текучести. В общем случае происходит некоторая эволюция поверхности текучести, которая описывается законом упрочнения материала, выражающемся в виде равенства
.
(5.19)
Здесь параметр текучести стал переменной
величиной, зависящей от параметра
упрочнения
,
и отвечает за расширение поверхности
текучести при пластическом деформировании,
так что
.
Тензор
,
называемый иногда тензором микродеформаций
отвечает за расположение оси симметрии
поверхности текучести. Если все его
компоненты нулевые, мы имеем изотропное
упрочнение – всестороннее расширение
поверхности текучести. В противном
случае при пластическом деформировании
поверхность сдвигается либо как жесткое
целое (кинематическое упрочнение), либо
одновременно с расширением (комбинированный
случай).
В качестве параметра упрочнения обычно рассматривают либо работу пластической деформации (энергетический параметр упрочнения)
,
(5.20)
либо накопленную пластическую деформацию (параметр Одквиста)
.
(5.21)
Если считать, что упрочнение при пластическом деформировании развивается одинаково во всех направлениях и не зависит от гидростатического давления , можно переписать (5.19) в виде
.
(5.22)
В случае трансляционного упрочнения это выражение нескольку изменяется, поскольку необходимо учесть перемещение центра:
.
(5.23)
Для приращений
,
соответствующих приращению пластической
деформации, существуют некоторые
экспериментальные дифференциальные
зависимости. Самый простой вариант,
имеющий распространение – линейная
связь между тензорами
и
.
В более полном виде зависимость от деформации имеется в обеих частях равенства:
.
(5.24)
Если материал в начальном состоянии изотропен и его поведение зависит лишь от второго инварианта тензора напряжений, то есть от интенсивности касательных напряжений , закон упрочнения принимает вид
.
(5.25)
Законы упрочнения вида (5.24) удовлетворительно описывают упрочнение материала в довольно широких границах изменения пути нагружения. При необходимости можно ввести в рассмотрение дополнительные параметры, определяющие вид правой части. Экспериментальные исследования, впрочем, показывают, что правая часть, отвечающая за расширение поверхности текучести, в процессе деформирования претерпевает сравнительно небольшие изменения.