ПЛАСТИЧЕСКОЕ ДЕФОРМИРОРВАНИЕ МАТЕРИАЛОВ.

Физические основы. Экспериментальные методы. Математическое моделирование.

Глава 5. Упругопластическое деформирование твердого тела

1. Идеальные модели упругопластического статического растяжения. Изотропное и кинематическое упрочнение. Условия пластичности Треска, Мизеса, Кулона – Мора, Друкера – Прагера.

Для начала рассмотрим одномерный случай.

На практике диаграмма растяжения линейна только на упругом участке и площадке текучести, если таковая вообще имеется. Для мягких цветных металлов линейности не наблюдается даже в упругой области. В сущности, упругая область для них не может быть строго определена и потому ограничивается некоторыми принятыми техническими допущениями. Однако во многих случаях реальные свойства материала могут быть удовлетворительно приближены идеальными линейными моделями.

Самая простая из них – идеальная жесткопластическая (рис. 5.1.1. а) – рассмотрена в предыдущей главе. Единственная характеристика материала в ней – предел текучести . При разгрузке для такой модели мы получим вертикальный участок диаграммы, вся накопленная деформация после разгрузки сохраняется. Эту модель можно усложнить, заменив пластическое течение деформационным упрочнением (рис. 5.1.1. б), для определения которого вводится вторая характеристика материала – тангенциальный модуль . Разгрузка производится так же, как в модели без упрочнения.

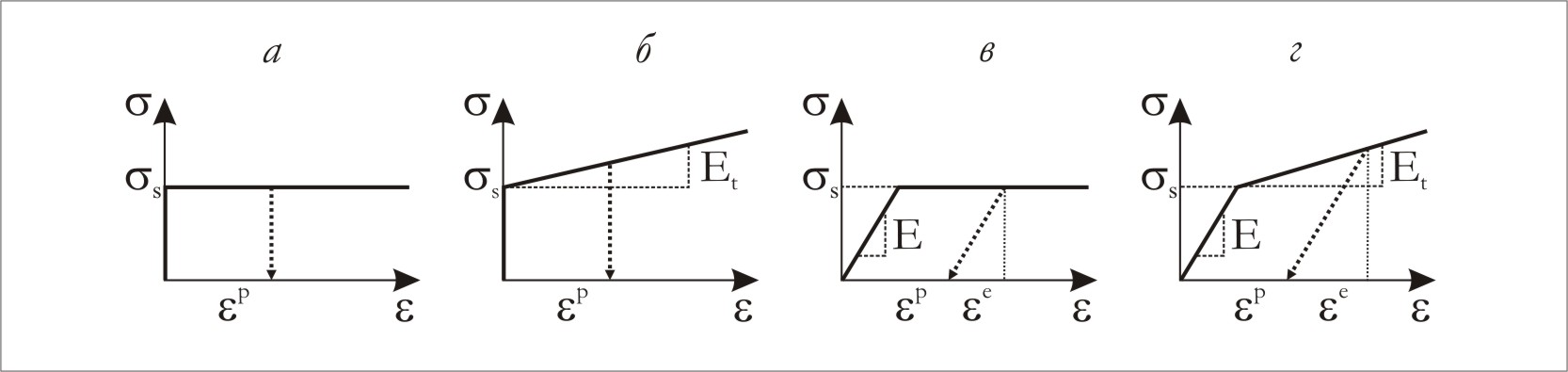
Рис. 5.1.1. Идеализированные диаграммы растяжения.

Более реальная модель – идеальная упругопластическая (5.1.1. в). Она определяется двумя характеристиками материала – пределом текучести и модулем Юнга . При разгрузке из пластической области на диаграмме образуется участок, параллельный упругому, и итоговая деформация образца, накопленная до момента разгрузки, складывается из двух частей – упругой деформации , исчезающей при разгрузке, и пластической деформации . Как и в жесткопластической модели, здесь можно ввести упрочнение, характеризуемое тангенциальным модулем (рис. 5.1.1. г). Между линейными участками упругости (задан модуль ) и деформационного упрочнения (задан модулем ) существует принципиальная разница. Если при разгрузке на упругом участке происходит возвращение по тому же пути, по которому шла нагрузка, то на пластическом участке разгрузка идет не вдоль прямой нагружения, а по отрезку, параллельному упругой части.

Упрочнение при нагрузке с одним знаком сказывается на поведении тела при обратном нагружении. Если предел текучести увеличивается одинаково и для растяжения и для сжатия, такое упрочнение называется изотропным (рис. 5.1.2. а). Если при увеличении предела текучести при растяжении предел текучести при сжатии уменьшается на ту же величину, такое упрочнение называется кинематическим (рис. 5.1.2. б), а само явление уменьшения предела текучести в одном направлении нагружения при увеличении в другом называется эффектом Баушингера.

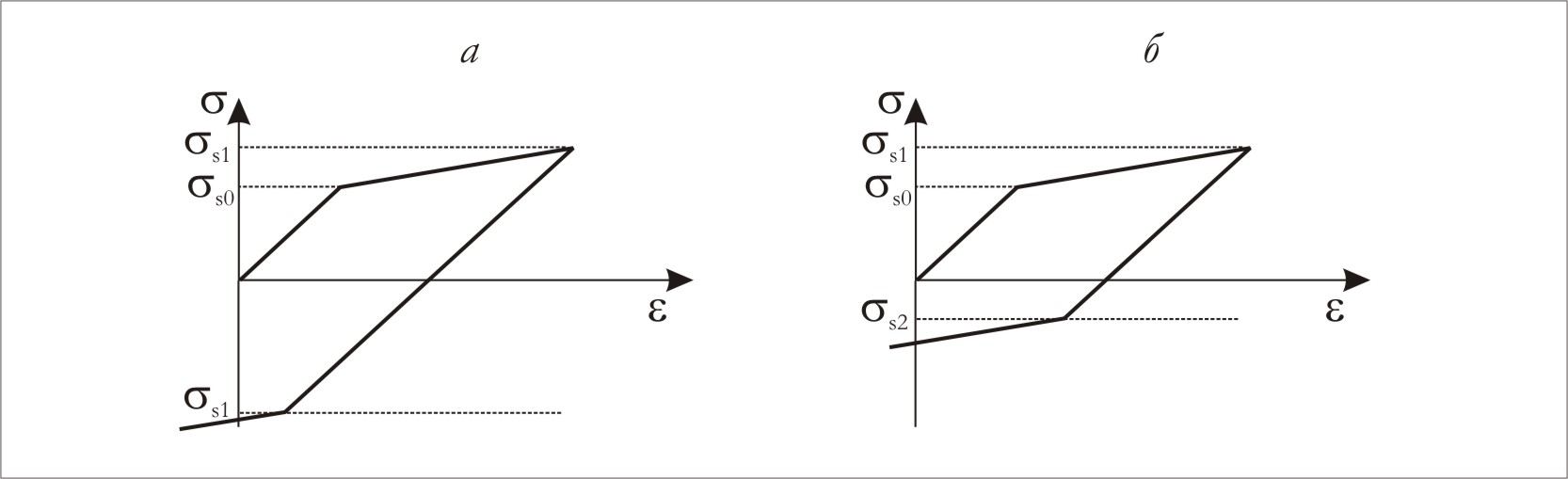
Рис. 5.1.2. Изотропное и кинематическое упрочнение.

В одномерном случае критерием текучести является выполнение равенства . В двумерном – . В трехмерном случае критерием текучести называется закон, определяющих границу упругого поведения материала при любых возможных комбинациях напряжений. Он выражается математически в виде равенства

, (5.1)

где – функция текучести, а – некоторый параметр текучести, который иногда переносят в левую часть, включая в . Уравнение (5.1) можно трактовать как уравнение поверхности в некотором пространстве, поэтому критерий текучести часто называют поверхностью текучести. В двумерном случае она вырождается в эллипс, в одномерном – в точку.

В силу природы функции текучести не любая функция может быть ею. На виду функции текучести накладываются следующие ограничения (если в качестве материала рассматривать изотропные металлы):

1. Функция текучести зависит только от трех главных напряжений или (что то же самое) от трех инвариантов тензора напряжений , то есть критерий текучести можно записать в виде

. (5.2)

2. Поскольку влияние среднего давления на процесс формоизменения пренебрежимо мало, можно (5.2) свести к виду

. (5.3)

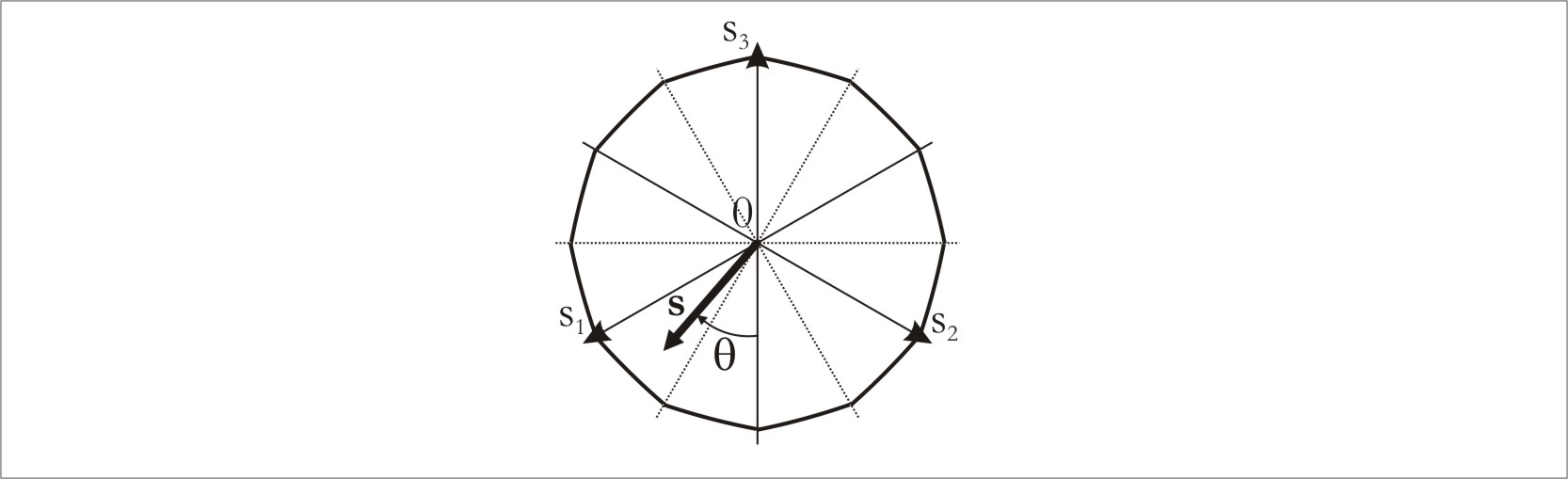
Рассмотрим условие текучести (5.3) в пространстве, где координатным базисом являются единичные векторы главных направлений тензора напряжений. Это пространство напряжений. Плоскость проходит через начало координат и наклонена одинаково ко всем осям. Она называется девиаторной плоскостью. Компоненты нормали к этой плоскость будут иметь вид .

В этом пространстве тензор напряжений отображается вектором , девиатор – вектором , который лежит в девиаторной плоскости, причем .

Прямая линия , называемая гидростатической осью, проходит через начало координат и перпендикулярна де6виаторной плоскости.

Уравнение (5.3) задает в пространстве напряжений цилиндрическую поверхность, осью которой является гидростатическая ось. След этого цилиндра на девиаторной плоскости называют кривой текучести (рис. 5.1.3).