Механические и электромагнитные колебания и волны
Гармонические колебания
1 Маятник совершает
свободные колебания, которые подчиняются
дифференциальному уравнению
.
Период колебаний маятника равен …
Решение:
Дифференциальное
уравнение свободных колебаний имеет
вид
,
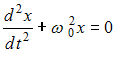где
собственная
круговая частота колебаний, которая
равна
.
Период колебаний 
.
В данной задаче
.
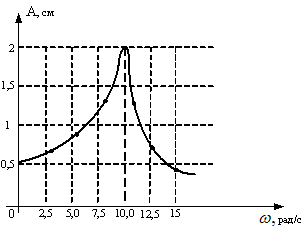
2 На
рисунке представлена зависимость
амплитуды вынужденных колебаний груза
массой 1 кг на пружине от частоты
вынуждающей силы при слабом
затухании.
Коэффициент
жесткости пружины в
равен
...
Решение:
На
графике представлена резонансная
кривая. Если частота вынуждающей силы
равна резонансной частоте, амплитуда
вынужденных колебаний достигает
максимального значения. При слабом
затухании резонансная частота практически
равна собственной частоте колебаний
пружинного маятника
.
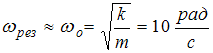Следовательно, 
.
3
Шарик, прикрепленный к пружине (пружинный
маятник) и насаженный на горизонтальную
направляющую, совершает гармонические
колебания.
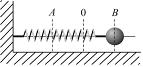На
графике представлена зависимость
проекции силы упругости пружины на
положительное направление оси Х
от координаты шарика.
В
положении В
энергия пружинного маятника в
равна
…
Решение:
В
положении В
пружинный маятник обладает потенциальной
энергией, кинетическая энергия равна
нулю. Потенциальную энергию можно найти
по формуле
,
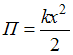где
коэффициент
жесткости пружины,
растяжение
(сжатие) пружины. Жесткость пружины
можно определить, используя график:
,
.
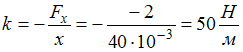Величину растяжения (сжатия) пружины в
положении В
также можно определить из графика:
.
4 Материальная
точка совершает гармонические колебания
по закону
.
Период
колебания точки равен…
Решение:
Зависимость
координаты материальной точки от времени
при гармонических колебаниях определяется
выражением
,
где
амплитуда,
круговая
частота,
начальная
фаза колебаний. Период колебаний равен
.
В данной задаче
следовательно,
период
5
Колебание материальной точки, возникающее
под действием внешней периодически
изменяющейся силы, происходит по
закону:
,
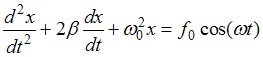где
–
коэффициент затухания;
и
–
циклические частоты соответственно
собственных и вынужденных колебаний;
–
амплитуда вынуждающей силы, отнесенная
к массе тела. Зависимость смещения
материальной
точки от времени имеет вид, показанный
на рисунке
Решение:
Уравнение
вынужденных колебаний
–
это линейное неоднородное дифференциальное
уравнение, решение которого равно сумме
общего решения однородного уравнения
и
частного решения неоднородного уравнения
.
Общее решение играет существенную роль
только в начальной стадии процесса
установления гармонических колебаний
с частотой
вынуждающей
силы (см. рис.). Из графика видно, что
амплитуда вынужденных колебаний
постепенно нарастает, и затем
устанавливается гармоническое колебание
с частотой вынуждающей силы:
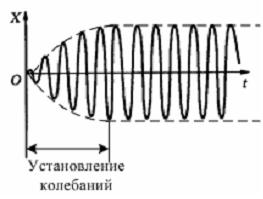
6 Маятник совершает
вынужденные колебания со слабым
коэффициентом затухания
,
которые подчиняются дифференциальному
уравнению
.
Амплитуда колебаний будет максимальна,
если частоту вынуждающей силы …
Решение:
Дифференциальное
уравнение вынужденных колебаний имеет
вид
,
где
коэффициент
затухания,
собственная
круговая частота колебаний;
амплитудное
значение вынуждающей силы, делённое на
массу;
частота
вынуждающей силы. При слабом коэффициенте
затухания (
)
амплитуда колебаний будет максимальна,
если частота вынуждающей силы совпадет
с собственной частотой колебаний
маятника (явление резонанса). Собственная
частота колебаний равна
,
частота вынуждающей силы -
.
Следовательно, частоту вынуждающей
силы необходимо уменьшить в 5 раз.
7 Складываются два гармонических колебания одного направления с одинаковыми периодами. Результирующее колебание имеет максимальную амплитуду при разности фаз, равной …