
Решение:
ЭДС
самоиндукции, возникающая в контуре
при изменении в нем силы тока I,
определяется по формуле:
![]() ,
где L
–
индуктивность контура. Знак минус в
формуле находится в соответствии с
правилом Ленца: индукционный ток
направлен так, что противодействует
изменению тока в цепи: замедляет его
возрастание или убывание. Таким образом,
ЭДС самоиндукции равна
,
где L
–
индуктивность контура. Знак минус в
формуле находится в соответствии с
правилом Ленца: индукционный ток
направлен так, что противодействует
изменению тока в цепи: замедляет его
возрастание или убывание. Таким образом,
ЭДС самоиндукции равна
![]() .
Абсолютная величина ЭДС самоиндукции
равна 0,03 В. Индукционный ток направлен
против часовой стрелки. При этом учтено
направление тока в контуре и его
возрастание со временем (что следует
из заданного закона изменения силы
тока).
.
Абсолютная величина ЭДС самоиндукции
равна 0,03 В. Индукционный ток направлен
против часовой стрелки. При этом учтено
направление тока в контуре и его
возрастание со временем (что следует
из заданного закона изменения силы
тока).
3
Полная система уравнений Максвелла в
интегральной форме имеет вид:
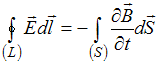 ,
,

 Следующая
система уравнений:
Следующая
система уравнений:
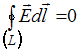 ,
,
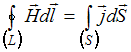 справедлива
для …
справедлива
для …
1) стационарных электрических и магнитных полей в отсутствие токов проводимости
2) стационарных электрических и магнитных полей при наличии заряженных тел и токов проводимости
3) стационарных электрических и магнитных полей в отсутствие заряженных тел
4) переменного электромагнитного поля при наличии заряженных тел и токов проводимости
Решение:
Сопоставление
первого уравнения рассматриваемой
системы с первым уравнением Максвелла
позволяет
сделать вывод о том, что скорость
изменения магнитного поля 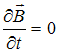 .
Следовательно, в данном случае магнитное
поле стационарно (
.
Следовательно, в данном случае магнитное
поле стационарно (![]() ).
Второе уравнение рассматриваемой
системы отличается от второго уравнения
Максвелла
тем,
что плотность тока смещения
).
Второе уравнение рассматриваемой
системы отличается от второго уравнения
Максвелла
тем,
что плотность тока смещения
 .
Следовательно, электрическое поле также
стационарно (
.
Следовательно, электрическое поле также
стационарно (![]() ),
а источником магнитного поля являются
только токи проводимости с плотностью
тока
),
а источником магнитного поля являются
только токи проводимости с плотностью
тока
![]() .
Источником электрического поля, согласно
третьему уравнению Максвелла, являются
электрические заряды с объемной
плотностью заряда
.
Источником электрического поля, согласно
третьему уравнению Максвелла, являются
электрические заряды с объемной
плотностью заряда
![]() .
Таким образом, рассматриваемая система
справедлива для стационарных электрических
и магнитных полей при наличии заряженных
тел и токов проводимости.
.
Таким образом, рассматриваемая система
справедлива для стационарных электрических
и магнитных полей при наличии заряженных
тел и токов проводимости.
4 Величину вектора магнитной индукции в данной точке магнитного поля можно определить по отношению …
1) силы, действующей со стороны магнитного поля на малый элемент длины проводника с током, к произведению силы тока на длину этого элемента, если он расположен в поле так, что это отношение имеет максимальное значение
2) времени поворота магнитной стрелки к ее длине
3) вращающего момента, действующего в магнитном поле на пробный контур с током, к магнитному моменту контура при такой его ориентации в поле, когда это отношение достигает максимального значения
4) силы, действующей на неподвижный точечный заряд, к величине заряда
Решение:
Величину
вектора магнитной индукции можно
определить, используя вращающий момент,
действующий на контур с током в магнитном
поле, силу Ампера, действующую на
проводник с током в магнитном поле, силу
Лоренца, действующую на заряженную
частицу, движущуюся в магнитном
поле.
Магнитная индукция численно
равна отношению вращающего момента,
действующего в магнитном поле на пробный
контур с током, к магнитному моменту
контура при такой его ориентации в поле,
когда это отношение достигает
максимального значения: 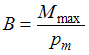 .
Магнитная
индукция численно равна отношению силы,
действующей со стороны магнитного поля
на малый элемент проводника с током, к
произведению силы тока на длину этого
элемента, если он расположен в поле так,
что это отношение имеет максимальное
значение:
.
Магнитная
индукция численно равна отношению силы,
действующей со стороны магнитного поля
на малый элемент проводника с током, к
произведению силы тока на длину этого
элемента, если он расположен в поле так,
что это отношение имеет максимальное
значение:
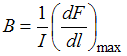 .
.
5 На
рисунке показана зависимость силы
тока i,
протекающего в катушке индуктивности,
от времени t.
|
Решение:
ЭДС
самоиндукции прямо пропорциональна
скорости изменения силы тока i
в
контуре:
![]() ,
где L
–
индуктивность контура. Следовательно:
1) если сила тока не изменяется со
временем, т.е. i
= const,
то
,
где L
–
индуктивность контура. Следовательно:
1) если сила тока не изменяется со
временем, т.е. i
= const,
то![]() ;
2) если сила тока возрастает, т.е.
;
2) если сила тока возрастает, т.е.
![]() >0,
то
>0,
то
![]() <0;
3) если сила тока убывает, т.е.
<0,
то
>0;
4)
если сила тока I
изменяется
со временем по линейному закону, т.е.
<0;
3) если сила тока убывает, т.е.
<0,
то
>0;
4)
если сила тока I
изменяется
со временем по линейному закону, т.е.
![]() ,
то
=
const, т.к. в этом случае
=
const.
Поэтому зависимость возникающей
в катушке ЭДС самоиндукции
,
то
=
const, т.к. в этом случае
=
const.
Поэтому зависимость возникающей
в катушке ЭДС самоиндукции
![]() от
времени правильно изображено на рисунке
от
времени правильно изображено на рисунке
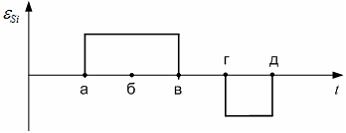
6 Вещество является однородным изотропным парамагнетиком, если магнитная восприимчивость …

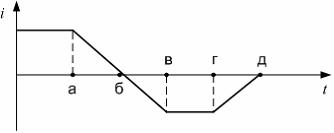 Изменение
возникающей в катушке ЭДС самоиндукции
Изменение
возникающей в катушке ЭДС самоиндукции