
- •21. Сила Ампера. Вектор магнитной индукции
- •22. Закон Био-Савара-Лапласа
- •23. Магнитное поле прямолинейного проводника с током.
- •24. Определение единицы силы тока-Ампера
- •26. Закон полного тока
- •27. Принцип закона полного тока к расчёту магнит поля тороида и длинного соленоида.
- •28. Сила Лоренца
- •29. Эффект Холла. Мгд генератор (магнитогидродинамический)
- •30. Магнитный поток. Теорема Остроградского-Гаусса.
- •3 1. Контур и виток с током в магнитном поле.
- •3 2. Явление электромагнитной индукции. Правило Ленца.
- •33. Фарадеевская и Максвеловская трактовка явления электромагнитной индукции
- •34° Самоиндукция. Индуктивность. Коэффициент взаимной индукции.
- •35° Магнитная энергия тока. Плотность магнитной энергии.
- •36. Магнитное поле в веществе. Намагниченность.
- •37. Напряженность магнитного поля.
- •38. Типы магнетиков. Диа- и парамагнетики.
- •39. Феромагнетики. Доменная структура. Техническая кривая намагниченности.
- •40. Ток смещения. С-ма ур-ий электродинамики Максвела в интегр. Форме.
- •41. Уравнения электродинамики Максвелла в дифференциальной форме.
- •42. Скорость распространения электромагнитных возмущений. Волновое уравнение.
35° Магнитная энергия тока. Плотность магнитной энергии.
Р ассмотрим
контур с индуктивностью L
и током в нем I.
Тогда с этим контуром сцеплен магнитный
поток Ф= I
L.При
изменении тока на dI
будет изменяться магнитный поток на
величину dФ=LdI
(L=const).
ассмотрим
контур с индуктивностью L
и током в нем I.
Тогда с этим контуром сцеплен магнитный
поток Ф= I
L.При
изменении тока на dI
будет изменяться магнитный поток на
величину dФ=LdI
(L=const).
Д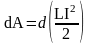 ля
изменения магнитного потока на величину
dФ
необходимо совершить работу dA
= IdФi
dA
=I
LdI
. Пусть ток меняется в контуре от 0 до I.
Работа по созданию магнитного потока
dФ
через поверхность, ограниченную контуром
ля
изменения магнитного потока на величину
dФ
необходимо совершить работу dA
= IdФi
dA
=I
LdI
. Пусть ток меняется в контуре от 0 до I.
Работа по созданию магнитного потока
dФ
через поверхность, ограниченную контуром
 .
Выражение называется собственной
энергией тока I
в
контуре с индуктивностью L.
Т.к. токи порождают магнитные поля, то
собственная энергия тока в контуре есть
энергия магнитного поля этого контура.
Тогда
.
Выражение называется собственной
энергией тока I
в
контуре с индуктивностью L.
Т.к. токи порождают магнитные поля, то
собственная энергия тока в контуре есть
энергия магнитного поля этого контура.
Тогда
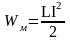 .
Получим
теперь энергию магнитного поля через
характеристики магнитного поля, т.е.
через
и
.
Получим
теперь энергию магнитного поля через
характеристики магнитного поля, т.е.
через
и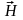 .
Получим
выражение Wм
на примере соленоида. Индуктивность
соленоида: L=μ0μn2V.
Индукция магнитного поля в соленоиде:
B=μ0μnI
I=B/μ0μn.
.
Получим
выражение Wм
на примере соленоида. Индуктивность
соленоида: L=μ0μn2V.
Индукция магнитного поля в соленоиде:
B=μ0μnI
I=B/μ0μn.
 - характеристика магнитного поля, т.к.
B=μ0μН,
то
- характеристика магнитного поля, т.к.
B=μ0μН,
то
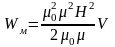
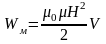
Обычно вводится пл-сть энергии магнитного поля – количество энергии в единице объема.
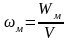
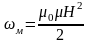 (
B=μ0μН),
(
B=μ0μН),
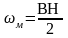
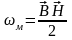
плотность
энергии электромагнитного поля
складывается из энергии электрического
поля и магнитного поля.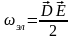 . Плотность энергии электромагнитного
поля:
. Плотность энергии электромагнитного
поля:

 ,
т.к.
,то
,
т.к.
,то

Lсоленоида=μ0μn2V
, откуда
 Гн/м ;
Гн/м ;

36. Магнитное поле в веществе. Намагниченность.
Магнитное
поле в в-ве может создаваться двумя
сп-бами: 1. макроскопическими токами
проводимости (ток по проводникам); 2.
микротоками обусловленными движением
электронов в атомах и молекулах. Все
в-ва обладают магнитными свойствами.
В-во или тело рассматриваются с точки
зрения магнитных свойств – магнетик.
Намагничивание – явл возникновения
объектного макроскопического магнитного
момента. Намагничивание характеризуется
намагниченностью. Намагниченность (
 )
– есть магнитный момент единицы объема.
)
– есть магнитный момент единицы объема.
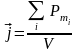 ,
,
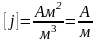
М олекулярный
ток: Рм=IS
олекулярный
ток: Рм=IS
В вакууме молекулярные токи отсутствуют и jвакуум=0
Вектор магнитной индукции создает макротоки и микротоки.
Существует три вида микроскопических магнитных моментов.
Электронный орбитальный магнитный момент – из-за вращения эл-нов вокруг ядер.
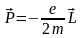
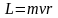
2. Электронный спиновой магнитный момент.
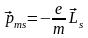 ,
где Ls
–
спиновой механический момент.
,
где Ls
–
спиновой механический момент.
3. Ядерный магнитный момент. Электронный орбитальный магнитный момент зависит от состояния электронов, и он либо равен 0 или порядка момента Бора:
 ,
,
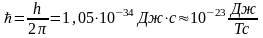
Спиновый магнитный момент = моменту Бора. Ядерный магнитный момент на 2 или3 порядка меньше магнетона Бора. В атомах и молекулах магнитные моменты отдельных атомов и мол, взаимно скомпенсир и потому сумма = 0 либо = порядку магнетона Бора.
37. Напряженность магнитного поля.
Теорема
о циркуляции вектора магнитной индукции
в вакууме ( )
допускает обобщение на магнитное поле
в веществе в виде:
)
допускает обобщение на магнитное поле
в веществе в виде:
 ,
где Iмакро
и Iмикро
–
алгебраическая сумма макро и микро
токов через поверхность S
ограниченных контуром L.
Покажем теперь, что Iмикро
связан
с намагниченностью
j:
,
где Iмакро
и Iмикро
–
алгебраическая сумма макро и микро
токов через поверхность S
ограниченных контуром L.
Покажем теперь, что Iмикро
связан
с намагниченностью
j:

Т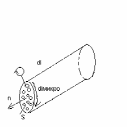 .е.
сумма микро токов через поверхность S
ограниченных контуром L
равна циркуляции вектора намагниченности
j.
Рассмотрим прямой круговой намагниченный
цилиндр длинной dl
и площадью поперечного сечения S.
Молекулярные токи внутри цилиндра текут
в противоположные стороны и поэтому
взаимноскомпенсированы. Нескомпенсированы
только те токи, которые выходят на
поверхность цилиндра и ни складываются
в поверхностный ток
.е.
сумма микро токов через поверхность S
ограниченных контуром L
равна циркуляции вектора намагниченности
j.
Рассмотрим прямой круговой намагниченный
цилиндр длинной dl
и площадью поперечного сечения S.
Молекулярные токи внутри цилиндра текут
в противоположные стороны и поэтому
взаимноскомпенсированы. Нескомпенсированы
только те токи, которые выходят на
поверхность цилиндра и ни складываются
в поверхностный ток

С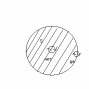 другой стороны полный магнитный момент
цилиндра по опр намагниченности равен:
другой стороны полный магнитный момент
цилиндра по опр намагниченности равен: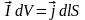 ,
,
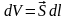
Так
как
и
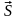 направлены в одну сторону, то dIмикро=jdl.
Вклад в циркуляцию намагниченность
дадут только те токи, которые нанизаны
как бусы на нитку. Тогда окончательно
можно написать:
направлены в одну сторону, то dIмикро=jdl.
Вклад в циркуляцию намагниченность
дадут только те токи, которые нанизаны
как бусы на нитку. Тогда окончательно
можно написать:
С
учетом последнего соотношения теорема
о циркуляции вектора магнитной индукции
принимает вид:
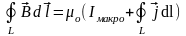 ,
,
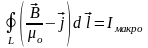
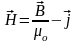 ,
,
 - теорема о циркуляции магнитного поля
- теорема о циркуляции магнитного поля
Циркуляция
вектора напряженности магнитного поля
вдоль произвольного замкнутого конура
равна результирующему макро току через
поверхность ограниченного этим контуром.
Для изотропных магнетиков связь
намагниченности j
и напряженности Н магнитного поля. Т.е.
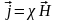 χ—безразмерная величина – магнитная
восприимчивость среды или вещества.
Подставим
в выражении для
χ—безразмерная величина – магнитная
восприимчивость среды или вещества.
Подставим
в выражении для
 :
:
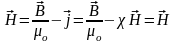 ,
,
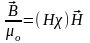 ,
,
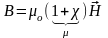
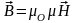 ,
,
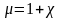
Если
среда не изотропная, то μ становиться
тензором:
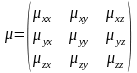
В
электричестве векторы
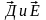 описывают поле:
описывают поле:
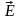 -
является истинным, он порождается и
связанный поляризованными зарядами.
-
является истинным, он порождается и
связанный поляризованными зарядами.
 -
вспомогательный вектор
-
вспомогательный вектор
В магнетизме:
- истинный – порождается микро и макро токами
- только макроскопическими токами
Природа вектора и и и одинаковы.
