
- •21. Сила Ампера. Вектор магнитной индукции
- •22. Закон Био-Савара-Лапласа
- •23. Магнитное поле прямолинейного проводника с током.
- •24. Определение единицы силы тока-Ампера
- •26. Закон полного тока
- •27. Принцип закона полного тока к расчёту магнит поля тороида и длинного соленоида.
- •28. Сила Лоренца
- •29. Эффект Холла. Мгд генератор (магнитогидродинамический)
- •30. Магнитный поток. Теорема Остроградского-Гаусса.
- •3 1. Контур и виток с током в магнитном поле.
- •3 2. Явление электромагнитной индукции. Правило Ленца.
- •33. Фарадеевская и Максвеловская трактовка явления электромагнитной индукции
- •34° Самоиндукция. Индуктивность. Коэффициент взаимной индукции.
- •35° Магнитная энергия тока. Плотность магнитной энергии.
- •36. Магнитное поле в веществе. Намагниченность.
- •37. Напряженность магнитного поля.
- •38. Типы магнетиков. Диа- и парамагнетики.
- •39. Феромагнетики. Доменная структура. Техническая кривая намагниченности.
- •40. Ток смещения. С-ма ур-ий электродинамики Максвела в интегр. Форме.
- •41. Уравнения электродинамики Максвелла в дифференциальной форме.
- •42. Скорость распространения электромагнитных возмущений. Волновое уравнение.
3 1. Контур и виток с током в магнитном поле.
Рассмотрим
работу перемещения проводника с током
в магнитном поле: На проводник с током
будет действовать сила Ампера и проводник
передвинется:

Элементарная работа при перемещении проводника:
 ,
,
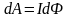
 Конечная
работа это:
Конечная
работа это:
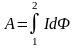 ,
,
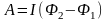
 Рассмотрим
прямоугольную рамку с током I
в
однородном магнитном поле
Рассмотрим
прямоугольную рамку с током I
в
однородном магнитном поле
 .
Покажем, что в общем случае рамка будет
вращаться. Это вид сбоку. Раз течет ток,
то возникает сила Ампера:
.
Покажем, что в общем случае рамка будет
вращаться. Это вид сбоку. Раз течет ток,
то возникает сила Ампера:
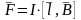 Сила Ампера будет действовать на ребра
a
перпендикулярные
к ним и к магнитной индукции и будет
только растягивать рамку.
Сила Ампера будет действовать на ребра
a
перпендикулярные
к ним и к магнитной индукции и будет
только растягивать рамку.
Вид сверху.
Оказывается,
что
-
М агнитное
поле создаваемое самой рамкой будет
совпадать с индукцией
.
Если контур повернется под действием
сил на угол
агнитное
поле создаваемое самой рамкой будет
совпадать с индукцией
.
Если контур повернется под действием
сил на угол
 ,
то будет совершена работа этими силами.
,
то будет совершена работа этими силами.
 ,
,
 ,
,
 .
С другой стороны, так как магнитный
поток через плоскую поверхность
ограничи-вается рамкой, магнитный поток
есть:
.
С другой стороны, так как магнитный
поток через плоскую поверхность
ограничи-вается рамкой, магнитный поток
есть:
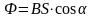 ,
где S-
площадь поверхности ограниченной
рамкой.
,
где S-
площадь поверхности ограниченной
рамкой.
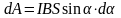 ,
получ:
,
получ:

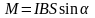 ,
,
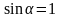
 получим макс момент:
получим макс момент:
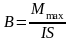 -
определение магнитной индукции. 1Тл =
-
определение магнитной индукции. 1Тл =


1-а
Тл это индукция такого однородного
магнитного поля, которое создает
максимальный вращательный момент
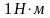 на рамку с током в 1 ампер и площадью
поверхности
на рамку с током в 1 ампер и площадью
поверхности
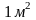 .
.
Поле должно быть однородным. Если контур в неоднородном поле, то кроме вращательного момента возникает сила втягивающая рамку в область сильного поля.
3 2. Явление электромагнитной индукции. Правило Ленца.
Т.к. электрический ток, т.е. упорядоченное движение электрических зарядов, создает магнитное поле, то и обратно-переменное магнитное приводит к возникновению тока. Явление электромагнитной индукции по Фарадею: «В замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. Этот ток называется индукционным». εi ~ dФ/dt. Фарадей показал, что ЭДС пропорциональна скорости изменения магнитного потока через поверхность, сцепленную с контуром: dФ/dt. Ленц в 1834 г. установил: «Индукционный ток всегда направлен так, что его магнитное поле противодействует изменению магнитного потока, пронизывающего поверхность контура». Объединим закон Фарадея и правило Ленца в СИ: εi = −dФ/dt. εi в замкнутом проводящем контуре равна скорости убывания магнитного потока через поверхность, ограниченную контуром. Если контур состоит из N витков, то изменение ЭДС равно сумме ЭДС, возникающему в каждом витке, тогда вводят полный магнитный поток: Ψ = ∑Фк, к=1. εi = − dΨ/dt, εi = −NdФ/dt.
П олучим
закон электромагнитной индукции, как
следствие закона сохранения энергии:
олучим
закон электромагнитной индукции, как
следствие закона сохранения энергии:
Если
рамка не закреплена,то она будет
вращаться, и за dt
Fa
совершит работу dA:
dA
= IdФ.
В рамке выделится тепло Джоуля-Ленца:
 .
По
закону сохра-нения энергии: сумма dA
и dQ
равна работа источника тока. εIdt=
IdФ+
I2
Rdt,
εdt=dФ=IRdt,
εi
= −NdФ/dt
.
По
закону сохра-нения энергии: сумма dA
и dQ
равна работа источника тока. εIdt=
IdФ+
I2
Rdt,
εdt=dФ=IRdt,
εi
= −NdФ/dt
I =(ε−
dФ/dt)/R,
− dФ/dt=
εi,
I=
(ε+
εi
)/R.
При
помещении массивных проводников в
переменное магнитное поле, в них возникают
вихревые токи. Получим теперь явление
электромагнитной индукции, как следствие
действия силы Лоренца на проводники,
движущиеся в магнитном поле. Пусть
участок проводника помещен в магнитное
поле с индукц. В и проводник перпендикулярен
индукц. В. Пусть проводник движется со
скоростью V.
=(ε−
dФ/dt)/R,
− dФ/dt=
εi,
I=
(ε+
εi
)/R.
При
помещении массивных проводников в
переменное магнитное поле, в них возникают
вихревые токи. Получим теперь явление
электромагнитной индукции, как следствие
действия силы Лоренца на проводники,
движущиеся в магнитном поле. Пусть
участок проводника помещен в магнитное
поле с индукц. В и проводник перпендикулярен
индукц. В. Пусть проводник движется со
скоростью V.
F=qVBsinα. Под действием силы Лоренца электроны будут двигаться вниз, аток направлен вверх: F=qE, qVB=qE, E=VB
εi=U= −Δφ= −El= −BlV, E= Δφ /l, Δφ= El
εi=U= −BlV
