
- •21. Сила Ампера. Вектор магнитной индукции
- •22. Закон Био-Савара-Лапласа
- •23. Магнитное поле прямолинейного проводника с током.
- •24. Определение единицы силы тока-Ампера
- •26. Закон полного тока
- •27. Принцип закона полного тока к расчёту магнит поля тороида и длинного соленоида.
- •28. Сила Лоренца
- •29. Эффект Холла. Мгд генератор (магнитогидродинамический)
- •30. Магнитный поток. Теорема Остроградского-Гаусса.
- •3 1. Контур и виток с током в магнитном поле.
- •3 2. Явление электромагнитной индукции. Правило Ленца.
- •33. Фарадеевская и Максвеловская трактовка явления электромагнитной индукции
- •34° Самоиндукция. Индуктивность. Коэффициент взаимной индукции.
- •35° Магнитная энергия тока. Плотность магнитной энергии.
- •36. Магнитное поле в веществе. Намагниченность.
- •37. Напряженность магнитного поля.
- •38. Типы магнетиков. Диа- и парамагнетики.
- •39. Феромагнетики. Доменная структура. Техническая кривая намагниченности.
- •40. Ток смещения. С-ма ур-ий электродинамики Максвела в интегр. Форме.
- •41. Уравнения электродинамики Максвелла в дифференциальной форме.
- •42. Скорость распространения электромагнитных возмущений. Волновое уравнение.
21. Сила Ампера. Вектор магнитной индукции
О

 п
путем было устан, что движущиеся эл-кие
заряды, т. е. токи создают магнитные
поля. Магнитное поле проявляется под
действием сил магнитного взаимодействия.
Магнитное поле в отличие от эл-кого
действует только на движ заряды, на
покоящиеся заряды не действует. (монополь
– магнитный заряд) Сп-сть магнитного
поля вызывать мех силу в каждой точке
поля, действ на элемент тока Id(в-р)l
хар-тся магнитной индукцией (вектор) B.
Эл-т
тока Id(в-р)l
есть произв силы тока I
на беск малый отрезок проводника
d(в-р)l,
направл по току. dI(в-р)l
играет роль пробного заряда в
электростатике. Ампер эксп-но установил,
что сила d(в-р)F
действ на элемент тока Id(в-р)l
с индукцией (в-р) B
равна:
п
путем было устан, что движущиеся эл-кие
заряды, т. е. токи создают магнитные
поля. Магнитное поле проявляется под
действием сил магнитного взаимодействия.
Магнитное поле в отличие от эл-кого
действует только на движ заряды, на
покоящиеся заряды не действует. (монополь
– магнитный заряд) Сп-сть магнитного
поля вызывать мех силу в каждой точке
поля, действ на элемент тока Id(в-р)l
хар-тся магнитной индукцией (вектор) B.
Эл-т
тока Id(в-р)l
есть произв силы тока I
на беск малый отрезок проводника
d(в-р)l,
направл по току. dI(в-р)l
играет роль пробного заряда в
электростатике. Ампер эксп-но установил,
что сила d(в-р)F
действ на элемент тока Id(в-р)l
с индукцией (в-р) B
равна:
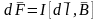 –
закон Ампера (сила Ампера). Если проводник
прямолинейный и магнитное поле однородное
(одинаковое в каждой точке), интегрируя
последнее выражение, получаем:
–
закон Ампера (сила Ампера). Если проводник
прямолинейный и магнитное поле однородное
(одинаковое в каждой точке), интегрируя
последнее выражение, получаем:
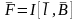 .
Направление силы Ампера (в-р)F
опр по правилу в-рного произведения.
Сила (в-р)F
┴-а пл-сти, в кот лежат в-ры l
и B
и напр силы (в-р)F
опред правилом правого винта: «если
рукоятка правого винта вращается от
первого вектора l
ко второму ве-ру B
на кратчайший угол, то поступательное
движ винта указ направление силы (в-р)F».
Модуль силы Ампера:
.
Направление силы Ампера (в-р)F
опр по правилу в-рного произведения.
Сила (в-р)F
┴-а пл-сти, в кот лежат в-ры l
и B
и напр силы (в-р)F
опред правилом правого винта: «если
рукоятка правого винта вращается от
первого вектора l
ко второму ве-ру B
на кратчайший угол, то поступательное
движ винта указ направление силы (в-р)F».
Модуль силы Ампера:
 .
Сила Ампера нецентральная, т. е. зависит
от ориентации проводника с током в
магнитном поле. Из з-на Ампера обычно
определяют магнитную индукцию (в-р) B.
Пусть проводник прямолинейный и ┴-ый
однородному магнитному полю (в-р) B:
F=IlB,
B=F/Il.
Магнитная индукция (вектор) B
– силовая, в-ная хар-ка магнитного поля,
числ равная силе, действ- со стороны
однородного магнитного поля на единицу
длины проводника, по которому течет ток
=1А и расположение проводника ┴-о напр
магнитного поля. Ед изм В в системе СИ
явл Тесла (Тл). 1 Тесла – магнитная
индукция такого однородного магнитного
поля, кот действует с силой 1Н на каждый
метр длины проводника с током 1А и
расположенное ┴-о магнитному полю:
1Тл=1Н/(1А*1м). Из опытов вытекает, что для
магнитных полей справедлив принцип
суперпозиции:
.
Сила Ампера нецентральная, т. е. зависит
от ориентации проводника с током в
магнитном поле. Из з-на Ампера обычно
определяют магнитную индукцию (в-р) B.
Пусть проводник прямолинейный и ┴-ый
однородному магнитному полю (в-р) B:
F=IlB,
B=F/Il.
Магнитная индукция (вектор) B
– силовая, в-ная хар-ка магнитного поля,
числ равная силе, действ- со стороны
однородного магнитного поля на единицу
длины проводника, по которому течет ток
=1А и расположение проводника ┴-о напр
магнитного поля. Ед изм В в системе СИ
явл Тесла (Тл). 1 Тесла – магнитная
индукция такого однородного магнитного
поля, кот действует с силой 1Н на каждый
метр длины проводника с током 1А и
расположенное ┴-о магнитному полю:
1Тл=1Н/(1А*1м). Из опытов вытекает, что для
магнитных полей справедлив принцип
суперпозиции:
 .
Поле (в-р) B,
порожденное несколькими движущими
зарядами или токами, равно в-рной сумме
полей (в-р)Bi,
порожденных каждым зарядом или током
в отдельности. Магнитное поле, как и
эл-кое, изображается магнитными силовыми
линиями – линиями (в-р) B.
Линии магнитной индукции (в-р) B
– это линии, касат к кот в каждой точке
совпадают с напр в-ра B.
Линии (в-р) B
всегда замкнуты, что указывает на
вихревой характер магнитного поля, на
отсутствие магнитных зарядов, на кот
могли бы начинаться и заканчиваться
силовые линии. По густоте силовых линий
судят о величине магнитного поля; там
где силовые линии редкие – магнитное
поле слабое.
.
Поле (в-р) B,
порожденное несколькими движущими
зарядами или токами, равно в-рной сумме
полей (в-р)Bi,
порожденных каждым зарядом или током
в отдельности. Магнитное поле, как и
эл-кое, изображается магнитными силовыми
линиями – линиями (в-р) B.
Линии магнитной индукции (в-р) B
– это линии, касат к кот в каждой точке
совпадают с напр в-ра B.
Линии (в-р) B
всегда замкнуты, что указывает на
вихревой характер магнитного поля, на
отсутствие магнитных зарядов, на кот
могли бы начинаться и заканчиваться
силовые линии. По густоте силовых линий
судят о величине магнитного поля; там
где силовые линии редкие – магнитное
поле слабое.
Линии индукции прямолинейного проводника с током представляют собой концентрические окружности, центры которых лежат на оси тока.
При поступательном движении правого винта направление вращения рукоятки винта указывает направление силовых линий.
22. Закон Био-Савара-Лапласа
З-н
БСВ даёт выражение для магнитной индукции
d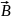 , создаваемой элементом I
d
, создаваемой элементом I
d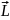 в точке, характеризуемой радиус-вектором
в точке, характеризуемой радиус-вектором
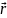 ,
проведённым из элемента проводника d
в искомую точку.
,
проведённым из элемента проводника d
в искомую точку.
Id
 |
|
µ |α
|
 |
|
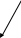 |
|
d
З-н
БСЛ:
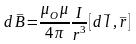
µ0 — магнитная постоянная=4π·10-7 Гн/м; µ — магнитная проницаемость среды
Модуль
индукции |dB|:
 .
Наряду с магнитной индукцией, можно
характеризовать напряжённость магнитного
поля. Дл изотропного случая:
.
Наряду с магнитной индукцией, можно
характеризовать напряжённость магнитного
поля. Дл изотропного случая:
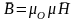
З-н
БСЛ для напряжённости
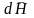 принимает вид:
принимает вид:

З-н БСЛ совместно с принципом суперпозиции допускает в принципе вычисление магнитных полей любой конфигурации токов.
