Вариант 18

1. На графике указана плотность распределения случайной величины X.

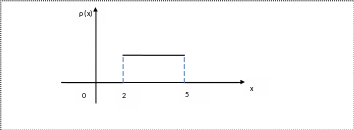
Найти дисперсию случайной величины X.

2. Найти и построить эмпирическую функцию распределения для выборки, представленной статистическим рядом

	1	3	6
	10	8	12

3. По паспортным данным на автомобильный двигатель, расход топлива на 100 км пробега составляет 10 л при среднем квадратичном отклонении 2 л. В результате совершенствования конструкции ожидается, что расход топлива уменьшится. Для проверки проведены испытания 25 случайно отобранных автомобилей с модернизированным двигателем: средний расход топлива на 100 км пробега составил 9,2 л. Используя 5 %-й уровень значимости, проверить гипотезу, утверждающую, что модернизация повлияла на расход топлива.

4. Известно, что D(a + bX) = b D(X). Доказать.

Вариант 19

1. Среди 10 лотерейных билетов имеется 4 билета с выигрышем. Наудачу покупают 2 билета. Написать закон распределения вероятностей числа выигрышных билетов среди купленных. Построить многоугольник распределения.

2. Найти несмещенную оценку дисперсии СВ X на основании данного распределения выборки:

x	2	7	9
n	8	14	10

3. Монету подбрасывают n раз. Вероятность выпадения герба при каждом подбрасывании равна p. В ходе опыта монета выпала гербом раз. Показать несмещенность оценки вероятности выпадения герба в каждом опыте. / Указание. Воспользоваться тем, что число успехов имеет распределение Бернулли (биномиальное распределение) /

4. Какова цель проверки гипотез?

Вариант 20

1. ДСВ X имеет закон распределения

x	0	1	2	3
p	0,1	0,3		0,2

Найти закон распределения СВ Y = sin( X) + 1.

2. Цена деления шкалы измерительного прибора равна 0,2. Показания прибора округляют до ближайшего целого деления. Найти вероятность, что при отсчете будет сделана ошибка, меньшая 0,04.

3. Найти минимальный объем выборки при котором с надежностью 0,925 точность оценки матожидания нормально распределенной генеральной совокупности по выборочной средней равна 0,2, если среднее квадратичное отклонение генеральной совокупности равно 1,5.

4. Средний диаметр подшипников должен составлять 35 мм. Однако для выборки из 82 подшипников он составил 35,3 мм при «исправленном» среднем квадратичном отклонении 0,1 мм. При 5 %-м уровне значимости проверить утверждение о том, что станок, на котором изготавливают подшипники, не требует подналадки.

Вариант 21

1. Плотность вероятности СВ X

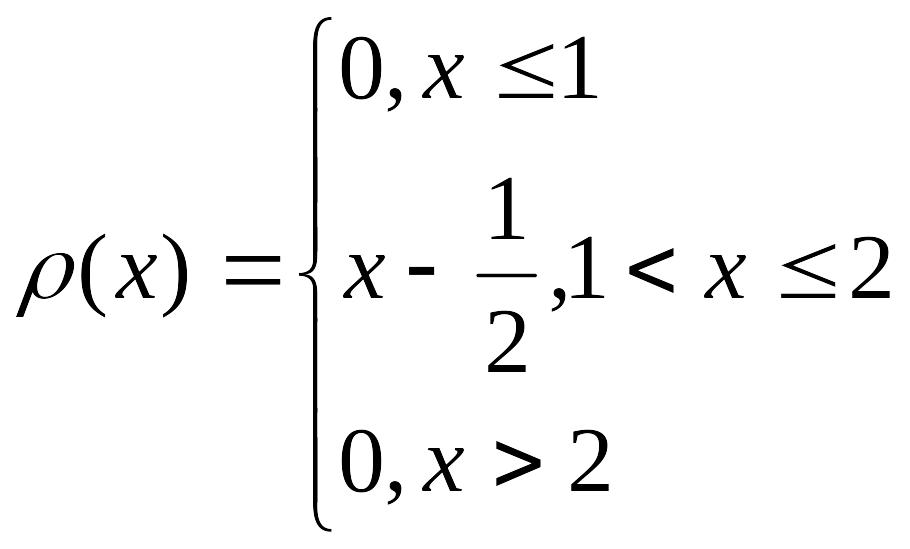
Найти функцию распределения и построить ее график.

2. Производится взвешивание некоторого вещества без систематических ошибок. Случайные ошибки взвешивания подчинены нормальному закону со средним квадратичным отклонением 20 г. Найти вероятность того, что взвешивание будет произведено с ошибкой, не превышающей по абсолютной величине 10 г.

3. При обследовании средней зарплаты работающих жителей города была сделана выборка из 100 человек, при этом оказалось, что средняя выборочная равна 80 у.е., а несмещенная выборочная дисперсия равна 12. Найти доверительный интервал уровня 0,95 для средней зарплаты X.

4. Что такое относительная частота события, как она связана с вероятностью?