Вариант 1
1. Д.С.В. принимает значения 1, 3, 5 с вероятностями 0,2; 0,3; 0,5. Найти функцию распределения, математическое ожидание ДСВ.
2. Из 1500 деталей отобрано 100, распределение которых по размеру задано в таблице.
Размер детали |
8 – 8,2 |
8,2 – 8,4 |
Количество |
20 |
80 |
Найти реализацию оценки матожидания и несмещенной оценки дисперсии.
3. В данном регионе кандидата в парламент поддерживает 60 % населения. При опросе общественного мнения было выбрано 1000 человек. С какой вероятностью можно утверждать, что доля избирателей из этой выборки, поддерживающих кандидата, отличается от истинной доли не более чем на 0,02?
4. Предположим, что вы отвергли нулевую гипотезу при уровне значимости 5 %. Верно ли утверждение о том, что вы автоматически отвергнете нулевую гипотезу при уровне значимости 1 %? Ответ поясните графически.
Вариант 2
1. Из партии объема 30 взята выборка объема 10. Если в партии 5 дефектных образцов, найти вероятность отсутствия брака в выборке.
2.
СВ имеет нормальный закон распределения
с параметрами: a
= 8,6;
= 0,5. Необходимо:
1) найти плотность вероятности этой СВ;
2) найти вероятность того, что она примет какое-нибудь значение, большее 9.
3. Фирма-поставщик в рекламном буклете утверждает, что средний срок безотказной работы предлагаемого изделия – 2900 часов. Для выборки из 50 изделий средний срок безотказной работы оказался равным 2720 часов при «исправленном» среднем квадратичном отклонении 700 часов. При 5 %-м уровне значимости проверить гипотезу о том, то значение 2900 часов является математическим ожиданием.
4.
Пусть x’
=
̶
— точечная оценка для M(X)
случайной величины X.
Будет ли эта оценка несмещенной,
асимтотически несмещенной? Привести
соответствующие доказательства.
Вариант 3
1. Дискретная случайная величина X задана законом распределения
x |
1 |
2 |
3 |
p |
0,2 |
|
0,3 |
Найти математическое ожидание случайной величины Y = 2X + 1.
2. СВ X распределена нормально со средним 10, а вероятность ее попадания в интервал (5,15) равна 0,8. Найти вероятность попадания X в интервал (9,10).
3. Произведено 5 независимых наблюдений над СВ X ~ N (a, 20). Результаты наблюдений таковы:
=
̶ 25,
= 34,
= ̶ 20,
=
10,
= 21. Найти оценку для a
= M(x),
а также построить для него
95 %-й доверительный интервал.
4. Покажите, что при наличии n наблюдений условием того, чтобы обобщенная формула
давала
несмещенную оценку для M(X),
является
.
Вариант 4
1.
Случайная величина X
задана плотностью вероятности
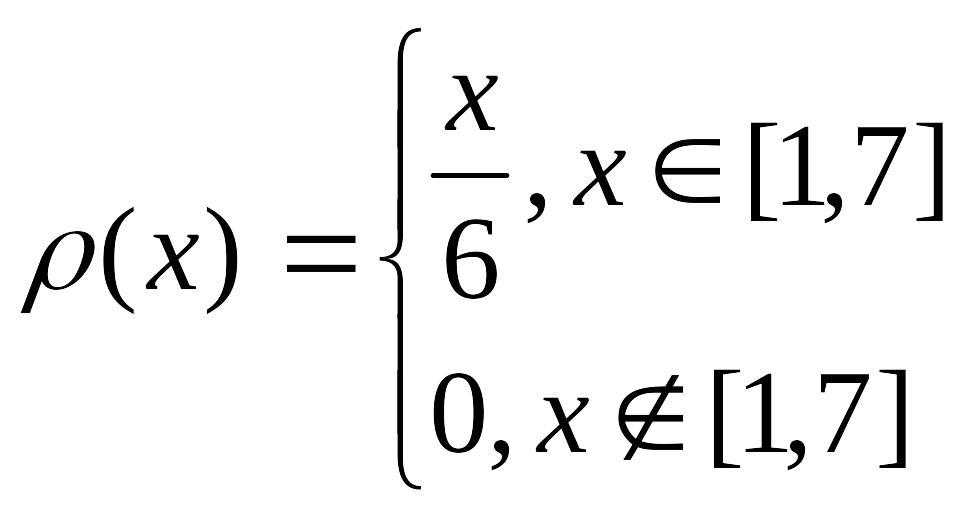
Найти P(2 < x <5), центр распределения.
2. Из 200 деталей отобрано 4, распределение которых по размеру следующее: 8, 7, 9, 5. Найти несмещенную оценку дисперсии и среднего квадратичного отклонения.
3. Фирма-изготовитель женских украшений, выпустив новый товар, утверждает, что 40 % покупателей купят эти украшения. В ходе 10-дневной рекламной распродажи в среднем приобрели украшения 29,5 % покупателей, «исправленное» среднее квадратичное отклонение составило 16,5 %. При 5 %-м уровне значимости оценить утверждение изготовителя товара.
4. Вообще говоря, при увеличении размера выборки дисперсия распределения оценки убывает. Правильно ли утверждать при этом, что оценка становится более эффективной? Ответ обосновать.