3.3. Методы экстраполяции и интерполяции

Интуитивные методы экспертной оценки просты и не требуют больших затрат. Однако они имеют существенный недостаток, который состоит в их субъективности. Метод «Дельфи» менее субъективен, но недостаточно точен. Чаще всего в практических целях используются формализованные методы: экстраполяции, интерполяции и моделирования.

Методы экстраполяции и интерполяции нашли широкое применение на практике, так как они просты, требуют малых затрат средств и времени. При этом составление прогноза возможно на небольшой статистической базе.

Экстраполяция – перенесение тенденции прошлого на будущее. Она позволяет показать, как изменится состояние объекта в будущем, если тенденции его развития будут такими же, как и в прошлом. Другими словами, метод основывается на предположении, что будущее есть продолжение настоящего, т. е. в будущем процесс будет развиваться точно так же, как в прошлом. При этом возможны небольшие изменения, которые должны учитываться при составлении прогноза.

Интерполяция – поиск промежуточных параметров объекта между уже известными значениями во времени или в пространстве.

Временной интервал, на который делается прогноз, называется сроком упреждения. Опыт прогнозирования показывает, что он должен быть как минимум в 3 раза меньше, чем статистическая база, которая используется для построения прогноза.

Считается, что если средняя относительная ошибка прогноза не превышает 10%, то его точность высокая, 10–30% – хорошая, 30–50% – удовлетворительная, более 50% – неудовлетворительная.

Метод подбора простых стандартных функций основан на анализе происходящих изменений и сопоставлении их с простыми алгебраическими функциями. Предположим, нам необходимо дать прогноз изменения значения у. При этом имеется ряд данных, которые показывают, как изменялся у в предшествующий прогнозу период (рис. 5).

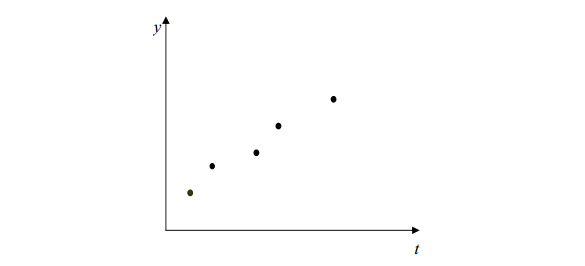
Рис. 5. Изменение значений y при изменении значений t

Результаты ранее полученных данных подвергаются регрессионному анализу. Он позволяет составить уравнение регрессии. В нашем случае оно будет иметь вид y = a + bt. Используя уравнение регрессии, строят теоретическую линию регрессии.

Для приведенного уравнения она следующий вид (рис. 6).

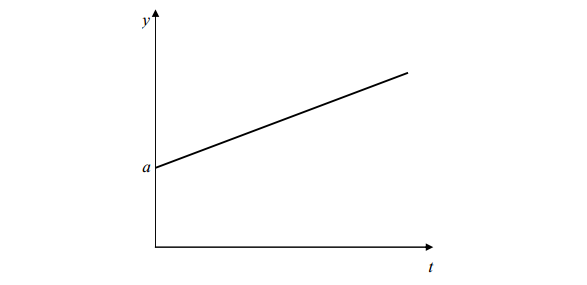
Рис. 6. Уравнение регрессии изменения y по t

Затем определяется коэффициент регрессии. Он показывает, как изменяется у при изменении t на единицу измерения. Таким образом, если предположить, что характер изменения значений t будет сохраняться в течение всего прогнозируемого периода, то можно с большой степенью достоверности оценить количественные значения y в будущем.

Приведенный пример изменения зависимости между двумя показателями является самым простым. Чаще всего теоретическая линия регрессии имеет более сложный вид (рис. 7).

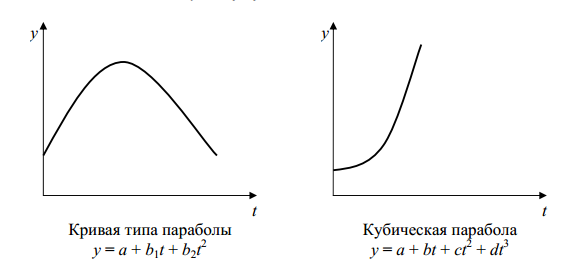
Рис. 7. Примеры стандартных алгебраических функций

Метод наименьших квадратов (МНК) – один из наиболее распространенных. Это объясняется его простотой, а при правильном использовании и относительной точностью. Он основан на анализе изменений в прогнозируемом объекте в период, предшествующий прогнозу.

Искомое значение прогнозируемого явления определяется по уравнению

y = aх + b,

где х – время упреждения от первого года базового периода;

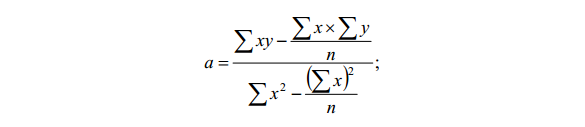
где n – число дат в базовый период;

y – значение прогнозируемого явления в базовый период;

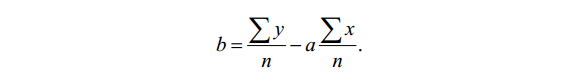
Ниже на основе метода наименьших квадратов сделан прогноз водопотребления в 2010 г. Вспомогательные данные приведены в табл. 1.

Год базового периода	Потребление воды Y, л/чел. в сут.	Х	ХY	Х2	n
1933 1937 1942 1960 1965 1970 1980 1990 2000 2004	171 182 211 224 208 210 229 231 237 239	1 5 10 28 33 38 48 58 68 72	171 910 2 110 6 272 6 864 7 980 10 992 13 398 16 116 17 208	1 25 100 784 1 089 1 444 2 304 3 364 4 624 5 184	1 2 3 4 5 6 7 8 9 10
Итого:	 2142	 361	 82 021	 18 876

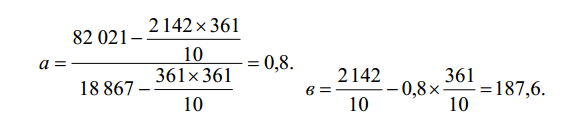
Таким образом, прогнозный показатель водопотребления в 2010 г. составит:

Y = 0,8 × 78 + 187,6 = 250 л/чел. в сут.