6.4.Позиционная система счисления

Для практического применения операции сложения – умножения натуральных чисел необходимо решить следующие проблемы.

• Определить функцию natural т.е. способ уникального символьного обозначения (кодирования) мощности любого абстрактного множества, т.е. способ записи любого натурального числа.

• Обозначения должны быть самоинтерпретирующимися, т.е. должна быть определена функция natural ^-1, обратная функции natural. Значением функции natural ^-1(n) является мощность вполне определенного множества, которую принято называть значением записи натурального числа.

• способ кодирования должен обеспечить возможность выполнения операций преобразования записей натуральных чисел, которые правомерно считать операциями сложения – умножения натуральных чисел.

По сути дела, речь идет о создании формального языка записи натуральных чисел – системы счисления натуральных чисел.

В принципе, для записи натуральных чисел можно использовать различные формальные языки.

Первоначально ЧЕЛОВЕКОМ была предпринята попытка использовать в качестве записи натуральных чисел символы алфавита естественного языка. Числа в церковно-славянских текстах записываются буквами. 30 букв алфавита имеют следующие числовые значения:

1	2	3	4	5	6	7	8	9
10	20	30	40	50	60	70	80	90
100	200	300	400	500	600	700	800	900

Очевидно, что в этом случае:

• представляется лишь небольшое множество натуральных чисел;

• об алгоритмах выполнения операций сложения-умножения речи не идет.

Теоретически удовлетворительной является примитивная система счисления натуральных чисел, используемая выше. Такая система счисления порождает формальный язык представления натуральных чисел, записи которого построены следующим образом. Алфавит формального языка состоит из одного знака: A ={1}. Любая последовательность единиц – правильная запись натурального числа в примитивной системе счисления. Более того, каждая примитивная запись является самоинтерпретирующейся: значение числа представляется количеством единиц в этой записи. Алгоритм сложения натуральных чисел, представленных в примитивной системе счисления, очевиден и чрезвычайно прост.

По-видимому, единственный недостаток примитивной системы счисления – большая длина записи, пропорциональная величине числа. Однако, этот недостаток настолько серьезен, что примитивная система счисления используется лишь для теоретических рассуждений.

Римская система счисления в качестве алфавита использует несколько собственных имен, каждое из которых является записью вполне определенного натурального числа: I- единица, V- пять единиц, X- десять единиц, L- пятьдесят единиц, C- единиц, M- тысяча единиц. Любая последовательность символов алфавита – правильная запись числа. Величина числа, представляемая записью, определяется как сумма величин представляемых собственными именами записи. Например, XXX – тридцать единиц (три раза по десять раз).

Примечание. На самом деле, конструкция записи числа в римской системе счисления несколько сложнее и здесь не обсуждается.

Римская система счисления позволяет записать любое натуральное число. Однако, записи чисел, величина которых больше тысячи становятся чрезвычайно длинными. Но главный недостаток римской системы счисления – отсутствие регулярности в конструкции записи величины числа, что не позволяет единообразно интерпретировать записи различных величин. Следствием этого является отсутствие эффективных алгоритмов выполнения арифметических операций над величинами, представленными в римской системе счисления. Тем не менее, она широко используется в случаях, когда нет необходимости совершать действия над величинами (нумерация глав, год выпуска в академических изданиях и т.д.)

Наиболее эффективной явилась позиционная система счисления натуральных чисел с основанием 10, изобретение которой приписывается арабам. По сути дела, это система алфавитной письменности, в которой алфавит состоит из десяти цифр. Запись целого числа без знака являет собой линейную строку символов алфавита – цифр, с универсальными правилами интерпретации любой записи. В дальнейшем оказалось, что основанием позиционной системы счисления может быть любое натуральное число большее единицы.

Ниже излагается концепция позиционной системы счисления натуральных чисел с произвольным основанием.

Выбирается произвольное, большее единицы, натуральное число, которое называется основанием системы счисления и обозначается как B. Числа меньшие B образуют базу системы счисления.

Для чисел базы выбираются уникальные символьные обозначения, которые называются цифрами. Интерпретация (натуральная величина) каждой цифры известна априори.

Имеется два формата символьной строки – обозначения величины натурального числа.

Формульный формат записи натурального числа. Запись любого натурального числа конструируется из цифр и знаков операций сложения-умножения. Такая символьная конструкция, которая представляет величину числа, называется формулой F_B натурального числа в позиционной системе с основанием B и имеет канонический вид:

F_B = (d_n-1B^n-1+d_n-2B^n-2+... d_iBⁱ+…+d₁B¹+d₀B⁰)_в. (15)

Здесь, d_i - цифра,  - знак операции сложения,  - знак операции умножения, B – основание системы, Bⁱ – основание системы счисления, умноженное само на себя i раз.

Рис. 9. Обозначение величины натурального числа в формате формулы и в формате записи.

Символьный формат записи натурального числа. В силу специфичности строения формулы натурального числа, последовательность коэффициентов формулы – последовательность цифр, также единственным образом представляет величину числа и называется записью значения натурального числа в В-ичной системе счисления:

n = (d_n-1d_n-2...d₁d₀)_в (16)

При этом, о коэффициенте d_i принято говорить как об i-м разряде натурального числа, а о значении n - как о количестве разрядов числа.

Замечательное свойство позиционной системы счисления – запись любого натурального числа конструируется из конечного числа знаков – цифр.

Конкретная формула натурального числа (запись натурального числа), по сути дела определяет способ выражения значения конкретного числа через априорно известные значения конечного числа цифр.

Примечание. Подобная система обозначений натуральных величин называется позиционной системой счисления, потому что в формуле числа каждое число базы, представленное цифрой, вносит в значение числа вклад, пропорциональный позиции, в которой эта цифра располагается.

Чрезвычайно важно, что позиционная система счисления позволяет определить алгоритмы выполнения операций сложения - умножения натуральных чисел как преобразование исходных символьных записей (операндов операций) в результирующие символьные записи (результаты операций). При этом формула F₃ результата операции обозначает значение суммы (рис.5): n₃ = n₁+n₂.

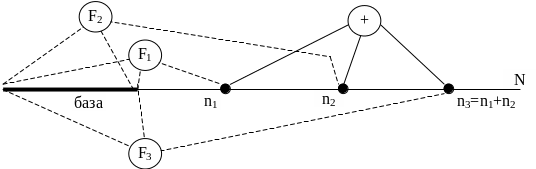
Рис. 10.Операция сложения натуральных чисел

Позиционная система счисления удовлетворяет всем требованиям к системе счисления, которые сформулированы выше. Прежде всего:

• позволяет сконструировать самоинтерпретирующуюся запись любого натурального числа;

• позволяет определить эффективные алгоритмы выполнения операций над записями, представляющими натуральные числа.

• для конструирования бесконечного множества записей натуральных чисел используется конечное (небольшое) множество знаков: цифры и основание (которое в любой системе принято обозначать как 10), знаки сложения, умножения и возведения в степень.

Исторически получили распространение следующие системы счисления натуральных чисел: десятичная (арабы, основание 10), двенадцатеричная (англичане, основание 12), шестидесятея ричная (время, основание 60). С появлением компьютеров в практику вошли двоичная, восьмеричная и шестнадцатеричная системы счисления.