6.2. Понятия измерительной шкалы, числа и измерения

Информация от артефактах реальных сущностей представляется в численной виде следующим образом.

Сущности, одинаковые с некоторой точки зрения, объединяются в предметные классы – таксоны.

Атрибут  таксона G обозначается как A^G_– необходимое, существенное, неотъемлемое ОБЩЕЕ СВОЙСТВО сущности. Характеристика (индивидуальное свойство) ^G_b конкретного элемента  таксона G - конкретизация общего свойства таксона для этого конкретного элемента. Например, атрибут (общее свойство) таксона группы студентов: "иметь возраст". Характеристика (индивидуальное свойство) конкретного студента: "конкретный возраст".

Атрибут таксона можно рассматривать как своеобразную переменную, область значений которой – домен атрибута A^G_, т.е. множество одинаковых с некоторой точки зрения характеристик образующих таксон сущностей (Рис.3).

Реальная сущность, входящая в таксон G, специфицируется набором {^G} индивидуальных свойств – характеристик.

Атрибуты подразделяются на числовые, значения которых определяются посредством измерения и нечисловые, значения которых просто обозначают те или иные характеристики. В дальнейшем, речь пойдет только о числовых атрибутах.

Для того, чтобы иметь возможность формальным образом обрабатывать информацию о сущности, ее характеристику ^G_b необходимо представить в виде единицы данных, т.е. обозначить числом d_, абстрагирующим специфику этой характеристики (Рис. 3).

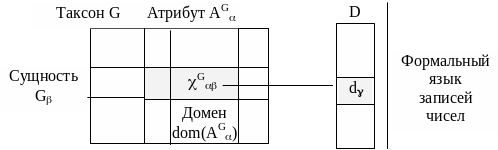
Рис. 3. Представление значения ^G_b атрибута A^G_ записью d_ числа

Числовая конкретизация атрибута получается в процессе измерения индивидуального свойства конкретного элемента таксона. Основой измерения служит измерительная шакала (в дальнейшем, просто шкала). Шкала – функция, отображающая домен атрибута A^G_ таксона G в множество D записей числа:

scale^: dom^G_  D (1)

Принято говорить, что каждая запись числа dD представляет (кодирует) вполне определенную конкретизацию атрибута – характеристику, сущности вполне определенного таксона.

Сказанное выше предполагает, что различаются понятие "число" и понятие "запись числа". Множество записей числа D являют собой формальный язык, символьные строки – предложения, которого конструируются вполне определенным образом.

Число определяется как функция, однозначно отображающая прототип числа в множество записей числа:

f: P  D (2)

Здесь, P – прототип числа (математическая или геометрическая фигура) определяющий тип числа, D – множество записей числа. Имя функции f, прототип P и множество записей числа D зависят от типа числа.

Примечание. Прототип числа P является моделью формального языка D. В отличие от процедуры вывода в модели формального языка – грамматике Хомского, здесь в качестве процедуры порождения предложений формального языка используется функциональное отображение ().

В практике вычислений используются различные типы чисел, такие как натуральные числа, вещественные числа и т.д.

Рис. 4.

6.3.Натуральное число

Прежде всего, по-видимому, в исторической перспективе сформировалось понятие натурального числа. ЧЕЛОВЕКУ необходимо было различать однородные предметы, вводя их обозначение - нумерацию, и также необходимо было манипулировать количествами и порядком расположения предметов.

Натуральное число — абстракция, используемая для количественной характеристики множеств реальных объектов, нумерации объектов, а также для обозначения места объекта в некоторой упорядоченной совокупности. Возникнув ещё в первобытном обществе из потребностей счёта, понятие натурального числа изменялось и обогащалось и превратилось в важнейшее математическое понятие. Письменными знаками (символами) для записи чисел служат цифры.

Прототипом натурального числа служит натуральное (линейно-упорядоченное) семейство A абстрактных множеств (Рис.1) мощность пустого множества обозначено знаком (цифрой) "0", мощность одноэлементного множества - знаком (цифрой) "1".

Существует две точки зрения на понятие "натуральное число".

Первая точка зрения - натуральное число являет собой средство для обозначения мощности (количества образующих элементов) любого абстрактного множества из K. В этом случае натуральное число называется кардинальным числом и определяется как функция card (конкретизация определения числа () для натурального числа), отображающая линейно – упорядоченное семейство множеств K в линейно-упорядоченное множество  записей кардинальных чисел (натуральный ряд  записей кардинальных чисел):

card: A   (3)

График определяющей число функции card приводится ниже.

Линейно-упорядоченное семейство множеств A	Натуральный ряд записей кардинальных чисел 
	0
СЛЕД()	0+1=1
СЛЕД(СЛЕД())	1+1=11
СЛЕД(СЛЕД(СЛЕД()))	11+1=111
…	…
СЛЕД(…(СЛЕД(СЛЕД(СЛЕД()))))	111…1+1=111…11

Здесь используется примитивная запись кардинального числа в виде пула единиц.

График функции card приведен также на рис. 5.

Рис. 5. Функция card, порождающая множество записей натурального числа.

Натуральный ряд записей кардинальных чисел можно получить посредством использования операции добавления единицы к записи кардинального числа:

111…1+1 = 111…11 (4)

Однако так порождаются только синтаксически правильные конструкции записей натурального числа. Семантика каждой такой записи – обозначение вполне определенного множества из K. Подобная семантика позволяет трактовать пул единиц 111…11– запись натурального числа, как представление мощности 111…11- элементного множества.

Вторая точка зрения - натуральное число являет собой средство для указания места элемента в линейно-упорядоченном абстрактном множестве MK. В этом случае натуральное число называется ординальным числом.

Место элемента в множестве M определяется процедурой "слева-направо рассчитайся". Назовем счетным состоянием множества M – подмножество уже пересчитанных элементов множества. Максимальное счетное состояние совпадает с множеством M (все элементы пересчитаны). На рис.6 показан ряд счетных состояний множества M, который совпадает с началом натурального ряда абстрактных множеств K. Таким образом, множество записей ординарных чисел определяется функцией ord и совпадает с множеством записей кардинальных чисел.

Рис. 6. Функция ord порождающая множество записей ординарных чисел

Разница между кардинальным и ординальным числом проявляется при интерпретации записи числа: 111…1. В первом случае – это обозначение мощности множества, во втором случае – обозначение положения элемента в множестве. В естественном языке это различие более существенно – используются количественные и порядковые числительные: множество из пяти элементов, пятый человек в шеренге.

Одинаковость формального языка записей кардинальных позволяет определять эти числа одной функцией:

card = ord= natural: A  (5)

Итак, мы определили формальный язык записей натуральных чисел (кардинальных и ординарных) – линейно-упорядоченное множество .

Каким образом использование натуральных чисел помогает решать прикладные задачи манипулирования реальными множествами?

Прикладная задача: Имеются две корзины с яблоками. Определить суммарное количество яблок в двух корзинах.

Задача определения суммарного количества яблок в двух корзинах на уровне реальных множеств решается посредством перемещения содержимого корзин A и B в корзину C, c последующим пересчетом количества яблок в корзине C. Очевидно, что это не лучший способ решения прикладной задачи.

Введение формализма натуральных чисел позволяет решить данную прикладную задачу, оперируя записями натуральных не прибегая к манипулированию содержимым реальных множеств.

Прежде всего, необходимо определить процедуру отображения реального множества - корзины с яблоками, в запись натурального числа, представляющего количество элементов в этом множестве.

На рис.7 показано, как реальные корзины с яблоками A и B отображаются в абстрактные множества M_A и M_B с мощностями _A и _B соответственно. Затем мощности этих множеств представляются записями натуральных чисел n_A и n_B.

По сути дела, предполагается существование двух функций: функция abstr отображает семейство реальных множеств в семейство абстрактных множеств M; функция natural отображает (кодирует) абстрактные множества из M в записи соответствующих натуральных чисел из . Функция natural суперпозиция двух функций: num.

Рис. 7. Раздельное объединение множеств и операция сложения натуральных чисел

Суперпозиция функций, natural abstr являет собой измерительную шкалу - функцию scale^power, отображающую семейство реальных множеств в записи натуральных чисел, представляющих мощности этих множеств:

n = scale^power(M); MM, n (6)

Таким образом, представление (кодирование) мощности реального множества осуществляется посредством вычисления функции () в заданной точке:

function scale^power(M);

counter:=0;

del(M);

while(not empty(M)) do

begin

counter:= counter +1;

del(M)

end;

scale^power:=counter

end.

Здесь используется вспомогательная операция исключения одного элемента из реального множества: del(<имя множества>). Также используется тестовая функция empty(<имя множества>) – принимающая значение "ИСТИНА" если множество M пусто.

Очевидно, что при выполнении функции () осуществляется пересчет элементов множества посредством последовательного удаления из него элемента за элементом. Выполнение пересчета может осуществляться как человеком, так и техническим устройством.

Вернемся к задаче определения суммарного количества элементов в двух реальных множествах. В алгебре абстрактных множеств существует операция раздельного объединения двух множеств:

M_C = M_AM_B (7)

Если  - мощность множества, то справедливо следующее равенство:

(M_C) = (M_AM_B) (8)

Примечание. Выше мы предположили, что элементы любых двух абстрактных множеств различны.

Введем в рассмотрение алгебру натуральных чисел (точнее, алгебру записей натуральных чисел):

Alg_ = <; +,> (9)

Здесь,  - множество записей натуральных чисел, + - знак операции сложения записей натуральных чисел,  - знак операции умножения записей натуральных чисел.

Императив операции сложения натуральных чисел записывается в виде символьной строки:

n_A+n_B = n_C (10)

Императив операции сложения предписывает исполнителю выполнить вполне определенный алгоритм преобразования двух символьных строк – слагаемых n_Aи n_B в символьную строку результат n_C.

Алгоритм преобразования символьных строк правомерно назвать алгоритмом сложения, если результирующая строка обозначает мощность (M_AM_B) раздельного объединения абстрактных множеств (Рис. 7). Если записи натуральных чисел представлены в примитивной кодировке, то алгоритм сложения натуральных чисел очевиден и чрезвычайно прост: результат сложения получается посредством присоединения записи второго слагаемого к записи первого слагаемого. Например, если n_A = 111и n_B = 11, то n_C = 11111.

Здесь мы имеем простейший случай формализации (моделирования) артефактов реального мира. Одна из проблем моделирования – адекватность формализма и реальности. В данном случае, насколько точно отражает результат преобразования символьных строк суммарное количество яблок в двух корзинах. Результат выполнения операции сложения натуральных чисел представляет суммарное количество яблок в двух корзинах, если записи натуральных чисел n_Aи n_B правильно представляют количество яблок в корзинах A и B. Говоря другими словами, если формализация исходных данных соответствует действительности, то результат формальных вычислений также соответствует действительности.

Рассмотрим еще одну прикладную задачу. В магазин привезли множество B ящиков, каждый ящик – множество A яблок. Определить количество яблок, завезенных в магазин. Для решения поставленной задачи необходимо выполнить n_B раз операцию сложения количества яблок в одном ящике:

n_A+ n_A+…+ n_A (11)

Многократное сложение заменяет операция умножения, которая определяется следующим образом. Реальные множества ящиков и содержимого ящиков абстрагируются множествами M_A и M_B, с соответствующими мощностями (M_A), (M_B).

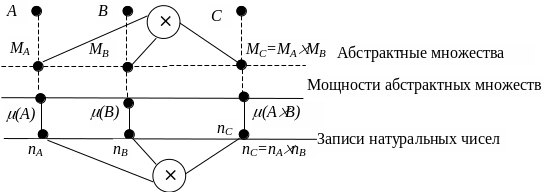
Рис. 8. Декартово произведение множеств и операция умножения натуральных чисел

Если M_A и M_B – абстрактные множества, то результат операции декартова умножения этих множеств являет собой множество M_C:

M_C=M_AM_B (12)

Если (M_A) и (M_B) – мощности множеств M_A и M_B соответственно, то мощность (C) результирующего множества M_C:

(M_C) = (M_AM_B) (13)

Очевидно, что общее количество яблок абстрагируется множеством M_C, которое является декартовым произведением двух множеств M_AM_B. Мощность результирующего множества - (M_C).

Если определены записи n_A и n_B натуральных чисел, представляющие количество яблок в каждом ящике и количество ящиков соответственно, то императив операции умножения записывается в виде символьной строки:

n_An_B = n_C (14)

Императив операции умножения предписывает исполнителю выполнить вполне определенный алгоритм преобразования двух символьных строк – сомножителей, n_Aи n_B в символьную строку – произведение n_C.

Алгоритм преобразования символьных строк правомерно назвать алгоритмом умножения, если результирующая строка n_C обозначает мощность (M_AM_B) произведения двух абстрактных множеств (Рис. 8).

Представление количественных (порядковых) характеристик натуральными числами позволяет различать однородные сущности. Например, говорить: "Возьмите корзину с пятью яблоками и оставьте корзину с десятью яблоками". Или говорить: "Наградите пятого человека в шеренге спортсменов".

Примечание. В практике вычислений принято вместо длинного термина "запись натурального числа" употреблять термин "натуральное число".