11.3.Алгебра логики и алгебра релейно - контактных схем

Существует большое число технологических процессов, состоящих из ряда следующих друг за другом операций. В состав того или другого технологического процесса могут входить отдельные операции в различной последовательности и различной продолжительности. Для автоматического управления такими процессами широко применяют электрические релейно-контактные схемы. С их помощью может осуществляться частичная и полная автоматизация управления многочисленными объектами народного хозяйства. Релейно-контактной называется электрическая схема, состоящая из соединенных определенным образом электрических контактов и реагирующих органов различных устройств, на которые контакты воздействуют.

Прибор, который получил название "электромеханическое реле" произвел переворот в области конструирования средств обработки информации. Основу реле составляет сердечник 1, выполненный из ферромагнитного сплава (Рис.38). На сердечнике располагается управляющая обмотка 2. Якорь реле 3 управляет работой контактной группы, которая состоит из нормально разомкнутого и нормально замкнутого контактов. Если по обмотке протекает ток, якорь притягивается к сердечнику замыкая нормально разомкнутые контакты и размыкая нормально замкнутые контакты. Если обмотка обесточена, якорь отпадает от сердечника, что приводит к замыканию нормально замкнутых контактов и размыканию нормально разомкнутых контактов.

Рис. 38 Электромеханическое реле

Таким образом, вход реле характеризуется высказыванием X, которое имеет два значения: "ток I через обмотку не идет" (X=0) и "ток I через обмотку идет" (X=1). Нормально разомкнутая контактная группа характеризуется высказыванием "ток i'' через контакт не идет" (Y'=0) и "ток i'' через контакт идет (Y''=1). Нормально замкнутая контактная группа также характеризуется высказыванием "ток i' через контакт не идет" (Y'=0) и "ток i' через контакт идет (Y'=1).

Вход X	Выход Н.р. контакт	Н.з. контакт
X=0	Y''=0	Y''=1
X=1	Y'=1	Y'=0

На языке алгебры логики это записывается следующим образом:

Y' = X; Y'' = X ()

В сильноточной электротехнике реле используют для управления (включение-выключение) больших напряжений небольшими управляющими напряжениями. В слаботочной электронике реле используют для реализации самых различных управляющий схем.

Впервые возможность применения алгебры логики для описания функционирования технических устройств была реализована в связи с распространением в человеческой практике релейно-контактных схем. Это привело к созданию технической дисциплины – теории релейно-контактных схем, опирающейся на аппарат алгебры-логики. В дальнейшем, с появлением бесконтактных электронных устройств – электронных реле, эта дисциплина переросла в теорию релейных схем.

Алгебра логики очень подошла для анализа и синтеза релейных схем. Можно говорить об алгебре релейно-контактных схем, высказываниями которой являются состояния контактов (замкнут-разомкнут) и аксиомы которой совпадают с аксиомами алгебры логики.

Примечание. По сути дела, алгебра релейно-контактных схем – одна из интерпретаций алгебры Буля.

Пример. Использование реле для реализации автоматических вычислителей элементарных логических функций.

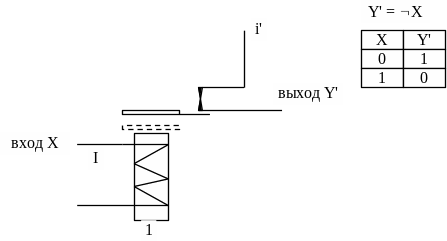
Рис. 39. Реализация логической функции "отрицание". Используется нормально замкнутый контакт

Рис. 40. Реализация логической функции "конъюнкция". Используются два нормально разомкнутых контакт. Значение функции 1 тогда и только тогда, когда, значение обоих аргументов равно 1.

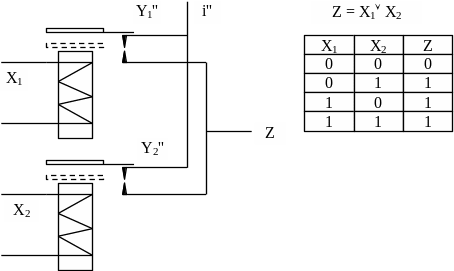
Рис. 41. Реализация логической функции "дизъюнкция". Используются два нормально разомкнутых контакта. Значение функции 1 если значение хотя бы одного аргумента равно 1.

Любая конкретная логическая функция представляется конкретным выражением алгебры логики, т.е. суперпозицией отрицаний, дизъюнкций и конъюнкций. Очевидно, что, можно получить автоматический вычислитель этой логической функции, реализовав соответствующую релейно-контактную схему.

Примечание. Таким образом, существует изоморфизм логических функций и релейно-контактных схем, вычисляющих эти функции.

Пример. Для логической функции () автоматически вычисляющая ее релейно-контактная схема показана на Рис.42.

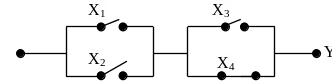
Рис. 42. Релейно-контактная схема автоматически вычисляющая логическую функцию: Y = (X₁X₂)&(X₃X₄)

В начале XX века релейно-контактные схемы начинают все шире и шире применяться в системах автоматики, защиты электротехнических систем, в связи. Каждая релейно-контактная схема, предназначенная для практических целей, являлась отдельным изобретением, поскольку не имелось общей теоретической концепции и принципа соответствующего моделирования.

Виктор Иванович Шестаков (1907—1987) — советский логик и теоретик-электротехник, в середине 1930-х гг. предложил интерпретацию булевой алгебры логики на релейно-контактных схемах. В. И. Шестаков высказал идею и сформулировал теорию релейно-контактных схем в 1934—35 годах. Аналогичные результаты в 1938 году представил в своей диссертации: "Символический анализ релейных и переключательных схем Клод Шеннон. По-видимому, В.И. Шестаков получил результаты раньше Шеннона, хотя диссертации (соответственно, кандидатскую и магистерскую) оба защитили в 1938 году, однако В. И. Шестаков опубликовал статьи, излагавшие его идею, только в 1941 г.

Заслуга В. И. Шестакова и К. Шеннона состоит в том что они предложили концепцию логического моделирования. Катализатором создания такой концепции явились все возрастающие запросы технического применения, рост сложности технических устройств. Простые технические устройства (электрические сети) не требовали особого теоретического аппарата при их конструировании; последний становится необходимым при конструировании сложных электрических сетей и, в дальнейшем, становится актуальной проблема оптимального синтеза управляющих систем различной проблемной ориентации. Техническая сторона этой проблемы требовала серьезных математических обоснований. Этой математической стороне проблемы собственно и посвятил свои работы В. И. Шестаков.

В начале сороковых годов советский ученый Михаил. Александрович Гаврилов продолжил создание научной методики проектирования релейно-контактных схем, получивших в те годы широкое практическое применение. Проводя анализ развития методов создания релейно-контактных схем, М. А. Гаврилов писал: "К числу первых работ, в которых делались попытки изыскать более рациональные методы проектирования релейно-контактных схем, следует отнести работы наших соотечественников А. Кутти и М. Цымбалистого (1928 г.) и некоторых иностранных специалистов, главным образом систематизировавших обычные интуитивные методы построения схем. Первые существенные достижения по пути развития научного обоснования методики построения схем были получены только тогда, когда был найден математический аппарат, отображающий соотношения, существующие в этих схемах".

Таким аппаратом стала алгебра логики. На возможность его использования впервые указал петербургский физик П. С. Эренфест в 1910 г. Позднее (в 1938 г.) В. И. Шестаков в СССР и одновременно К. Шеннон в США дали строгое обоснование возможности использования исчисления высказывании для описания релейно-контактных схем. Исходя из этих работ, М. А. Гаврилов создал стройную теорию анализа и синтеза одно- и многотактных релейно-контактных схем, являющуюся составной частью прикладной теории автоматов и дискретных устройств. За первой его работой (1943 г.) последовало много статей этого направления, которые были положены в основу диссертации на соискание ученой степени доктора технических наук (1946 г.).

Все результаты этих исследований были им систематизированы и оформлены в виде монографии "Теория релейно-контактных схем", выпущенной в свет в 1950 г. издательством АН СССР.

История развития кибернетики в СССР сохранила факты противодействия попыткам М.А. Гаврилова – в известном смысле последователя В.И. Шестакова – доказать правомерность использования методов математической логики (булевой алгебры) для расчета и проектирования релейно-контактных схем, используемых в автоматике.. Те, кто выступал против использования логико-математических методов в инженерной практике, обвиняли М.А. Гаврилова в "формализме" и даже идеализме. Подавляющее число коллег М.А. Гаврилова, как отмечает Д.А. Поспелов, отвергали его непонятные логические формулы. Докторская диссертация М.А. Гаврилова (1946 г.) оценивалась как идеологически вредная, протаскивающая идеалистическое мировоззрение и в том, что ее автор "льет воду на мельницу нашим зарубежным недругам". Лишь старая большевичка и уважаемый ученый С.А. Яновская смогла вывести М.А. Гаврилова из под удара. С высоты прошедших лет можно достаточно уверенно утверждать, что В.И.Шестаков и К. Шеннон открыли новое направление в науке независимо друг от друга, хотя В.И. Шестаков реализовал идею логического моделирования несколько раньше Шеннона. Также очевидно, что П. Эренфест и А. Накашима высказывали аналогичные идеи. [Поспелов]

В середине 1950-х годов М. А. Гавриловым были разработаны методы минимизации мостиковых контактных и контактно-вентильных схем, а также метод минимизации булевых функций, получивший известность как "метод проб М. А. Гаврилова". В связи с большой трудоемкостью минимизации возникла необходимость в разработке методов приближенной минимизации, годных для инженерной практики. М. А. Гаврилов предложил общий подход к построению методов синтеза такого типа, получивший название направленного поиска минимальных реализаций. За развитие этой теории, методов расчета и принципов построения релейных схем в 1958 г. Президиум АН СССР присудил М. А. Гаврилову премию им. П. М. Яблочкова.

Значительный период научной деятельности Геллия. Николаевича Поварова был также связан с разработкой методов синтеза управляющих контактных схем, результатом чего стало создание математической теории синтеза контактных схем с одним входом и несколькими выходами. Продолжением исследований в области сетей связи стала разработка теории кумулятивных сетей. На протяжении всей жизни Г. Н. Поваров интересовался вопросами математической логики и исследованием булевых функций, методами их сравнения и минимизации. Предложил новую концепцию событийной логики.

Под редакцией Г. Н. Поварова вышли переводы на русский язык классической книги Н. Винера «Кибернетика, или управление и связь в животном и машине» (1-е издание вышло в 1958 году, 2-ое — в 1968 г.).

"Вопросы истории естествознания и техники",

2007, № 3.