8.Аналоговые и цифровые вычислители
На самой заре развития информатики были сформулированы две принципиально различные парадигмы вычисления элементарных функций: аналоговая и цифровая.
Аналоговая парадигма предполагает представление числовой величины величиной характеристики какой-либо физической сущности. При этом устанавливается соответствие между величиной числа и характеристикой физической сущности. Аналоговое представление позволяет выполнять операции над числами как операции над характеристиками физических сущностей.
Пример: вещественное число представляется длиной отрезка счетной линейки; вещественное число представляется величиной электрического тока в электронном сумматоре и т.д.
Развитием парадигмы аналоговой обработки данных является создание аналоговых моделей реальных физических объектов. Суть дела состоит в том, что модель и ее реальный прототип реализованы на различных физических принципах, но поведение обоих описывается одними и теми же алгебраическими (дифференциальными) уравнениями. Таким образом, экспериментируя с моделью, можно интерпретировать полученные результаты применительно к реальному прототипу.
Пример. Построенная определенным образом электронная схема, моделирует колебательные процессы физического маятника.
Цифровая парадигма представляет числовую величину состоянием какого-либо технического дискретного носителя данных. Например, состоянием регистра компьютера. Цифровое представление позволяет выполнять операции над числами как операции изменения состояний технического носителя.
Развитием парадигмы цифровой обработки данных привело, в конечном итоге, к созданию программно-управляемых машин преобразования данных – компьютеров.
9.Простейшие вычислители
9.1.Аналоговые вычислительные линейки
Простейшим аналоговым вычислительным прибором является так называемая арифметическая линейка, позволяющая автоматически выполнять операции сложения и вычитания. Такая линейка состоит из двух частей: основание - нижняя неподвижная часть и движок - верхняя подвижная часть (рис. 7). На основание нанесена числовая линейная шкала (рис.7 a). Каждый сектор s (между двух длинных соседних рисок) представляет собой единицу. Сектор s состоит из десяти интервалов, каждый из которых имеет длину l. Таким образом, длина сектора s = l*10. Каждая длинная риска помечена целым числом n, которое представляет порядковый номер этой риски в последовательности рисок. Длина части основания, заключенной между рисками 0 и n, равна Ln = s*n = (10*l)*n. Аналогичная числовая шкала нанесена на движок.
Таким образом, можно утверждать, что вещественное число r = n.m с точностью до одного десятичного знака представляется аналогом - длиной отрезка базы или движка: Ln.d = s*n+l*m.
Сказанное выше позволяет выполнять операцию сложение двух вещественных чисел посредством операции сложения представляющих их длин. Операция сложения двух вещественных чисел реализуется следующим образом (рис.21 b).
На числовой шкале основания откладывается длина Lr1 представляющая величину первого слагаемого – риска n1.m1.
Начало движка устанавливается на эту риску.
В вычислительной линейке имеется подвижный визир, посредством которого на шкале движка устанавливается длина Lr2 представляющая величину второго слагаемого – риска n2.m2.
По визиру на шкале основания считывается результат сложения длин.
Если запись первого слагаемого: r1 = n1.m1, и запись второго слагаемого: r2 = n2.m2, то в результате сложения длин получается следующий результат:
L1+L2 = s*n1+l*m1+s*n2+l*m2 = s*(n1+n2) +l(m1+m2) r1+r2
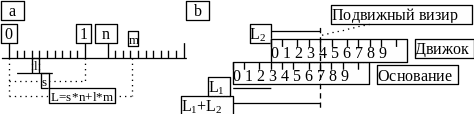
Рис. 21. Сложение на арифметической линейке: 3+4 =7
Арифметическая линейка позволяет также выполнять операцию вычитания двух вещественных чисел. Для выполнения операций умножения и деления такая линейка не предназначена.
Этапом в развитии средств автоматизации вычислений явился выпуск Джоном Непером в 1614 г. научного труда "Описание удивительной таблицы логарифмов". В своем труде Джон Непер не только теоретически обосновал логарифмическую функцию, но и разработал практическую таблицу двоичных логарифмов. Изобретение упростило выполнение операций умножения и деления, так как при умножении достаточно сложить логарифмы чисел.
Логарифмическая линейка, точно также как и арифметическая линейка имеет неподвижную основу и подвижный движок. На основе располагаются две числовые шкалы: линейная шкала чисел и логарифмическая шкала чисел. В этом случае длина на логарифмической шкале представляет логарифм числа. Сложение длин, представляющих два сомножителя, дает в результате длину, представляющую произведение сомножителей. Результатом вычитание длин, представляющих делимое и делитель, является длина, представляющая частное от деления.
Примечание. По сути дела пара шкал (как на основе, так и на движке) являет собой таблицу логарифмов и антилогарифмов.
РРис.
22. Умножение на логарифмической линейке:
2*3 + 6
Таким образом, логарифмическая линейка автоматизирует выполнение четырех арифметических операций.
Простота пользования и дешевизна изготовления объясняет тот факт, что логарифмическая линейка, в разных модификациях, стала необходимым инструментом инженера и научного работника и дожила до 80-х годов XX века. Адекватной заменой логарифмической линейке стал только электронный микрокалькулятор. Однако, последний относится к классу цифровых вычислительных приборов.
Рис. 23. Типичная логарифмическая линейка
Существенным недостатком логарифмической линейки (равно как и всех аналоговых вычислителей) является малая точность вычисления, которая определяется длиной интервала разметки численной шкалы. Если длина интервала один миллиметр, то гарантируется точность вычисления в один десятичный знак после запятой. Увеличивая общую длину линейки можно получить большую точность. В конструкторских бюро, где проводились серьезные вычисления, существовали "точные" логарифмические линейки, вплоть до двухметровой длины. Но подобный способ увеличения точности вычислений имеет свой предел и является тупиковым. Вычисления, теоретически, с любой точностью можно реализовать только на цифровых вычислителях.