
- •Нижегородский государственный университет им. Н.И. Лобачевского
- •1.Предисловие
- •2.Замечания по терминологии
- •3.Кибернетика и информатика
- •4.Предпосылки информатики
- •4.1.Мечта человека об искусственном человеке
- •4.2.Усилители физической и умственной деятельности человека
- •4.3.Ключевые проблемы информатики
- •5.Формализация естественного языка как средства общения.
- •6.Формализация физических характеристик среды обитания
- •6.1.Дискретные и непрерывные множества
- •6.2. Понятия измерительной шкалы, числа и измерения
- •6.3.Натуральное число
- •6.4.Позиционная система счисления
- •6.5.Натуральная числовая прямая
- •6.6.Целые числа (положительные и отрицательные)
- •6.7.Вещественные числа
- •7.Формализация физических зависимостей
- •7.1.Функции
- •7.2.Элементарные функции
- •7.3.Элементарная алгебра, аналитические и численные вычисления
- •8.Аналоговые и цифровые вычислители
- •9.Простейшие вычислители
- •9.1.Аналоговые вычислительные линейки
- •9.2.Цифровой абак и русские счеты
- •9.3.Цифровые механические арифмометры
- •9.4.Хронология событий.
- •10.Аналитические машины Чарльза Беббиджа.
- •11.Формализация рассуждений
- •11.1.Логика рассуждений
- •11.2.Логические функции и алгебра логики
- •11.3.Алгебра логики и алгебра релейно - контактных схем
- •12.Накануне компьютерной эры
- •12.1. Зарождение цифровых систем управления
- •12.2.Перфокарточные сортировальные машины
- •12.3.Методология моделирования
- •13.Теоретические модели вычислений
- •13.1.Алгоритм и его свойства
- •13.2.Проблема слов в ассоциативном исчислении
- •13.3.Нормальный алгоритм Маркова
- •13.4.Рекурсивные функции
- •13.5.Машина Тьюринга
- •13.6.Равнодоступная адресная машина
- •14.Пионеры зарубежной компьютеризации
- •15.Становление информатики в России. Борьба за признание
- •16.Два типа электронных вычислительных машин
- •16.1.Аналоговая вычислительная машина (авм)
- •16.2.Цифровая электронная вычислительная машина (компьютер, эвм)
- •16.3.Аналог или цифра
- •17.Пионеры отечественной компьютеризации
- •18.Становление информатики в России. Начальный период
- •19.Оригинальные отечественные серийные эвм (компьютеры)
- •19.1.Эвм Стрела
- •Элементная база
- •Программное обеспечение
- •Описание машины
- •Технико-эксплуатационные характеристики
- •Особенности эвм
- •19.2.Семейство эвм "м-20"
- •Структура эвм
- •Элементная база
- •Программное обеспечение
- •Технико-эксплуатационные характеристики
- •Особенности машины
- •Об использовании эвм м-20
- •Описание машины
- •Элементная база
- •Программное обеспечение
- •Технико-эксплуатационные характеристики
- •Особенности эвм
- •19.3.Семейство эвм "бэсм"
- •19.3.1.Бэсм-1
- •Структура эвм
- •19.3.2.Бэсм-2
- •Структура эвм
- •19.3.3.Бэсм-4
- •Структура эвм
- •Элементная база
- •Программное обеспечение
- •Технико-эксплуатационные характеристики
- •19.4.Семейство эвм "Минск"
- •19.4.1.Минск-1
- •19.4.2.Минск-2
- •19.4.3.Минск -22
- •19.4.4.Минск-23
- •19.4.5.Минск-32
- •Описание машины
- •Программное обеспечение
- •Технико-эксплуатационные характеристики
- •Особенности эвм
- •19.5.Семейство эвм "Урал"
- •19.5.1.Урал-1, Урал-2, Урал-3, Урал-4
- •Описание машины
- •Элементная база
- •Программное обеспечение
- •Основные эксплуатационно-технические данные
- •Особенности эвм
- •19.5.2.Урал-11, Урал-14, Урал-16
- •Описание машины
- •Элементная база
- •Программное обеспечение.
- •Основные эксплуатационно-технические данные машины “Урал-11”
- •Особенности эвм
- •19.6.Эвм "Весна" и "Снег"
- •19.7.Эвм бэсм-6
- •Описание машины
- •Элементная база
- •Программное обеспечение
- •Технико-эксплуатационные характеристики
- •Особенности машины
- •19.8.Многопроцессорные вычислительные комплексы "Эльбрус"
- •Описание машины.
- •Элементная база
- •Программное обеспечение
- •Типовые комплектации
- •Производительность
- •19.9.Управляющие эвм
- •20.Эволюция элементарной базы и поколения эвм
- •20.1.Базисные логические элементы
- •20.2.Элементы регистровой памяти
- •20.3.Элементы памяти на магнитных сердечниках.
- •20.4.Интегральные схемы
- •20.5.Поколения эвм
- •21.Американская система ibm-360
- •22.Семейство Ряд "ес эвм"
- •22.1.Хронология создания
- •22.2.Ес эвм. Крупнейший промах или всеобщее счастье?
- •23.Автоматизация программирования
- •23.1.От двоичных кодов к ассемблерам - языкам символьного кодирования
- •Ассемблеры
- •Программы - загрузчики
- •23.2.Языки программирования высокого уровня
- •23.3.Трансляция программ
- •24.Первые компьютеры Сарова
- •25.Начало компьютеризации Нижегородского госуниверситета
- •26.Они были первыми
- •26.1.Конрад Цузе
- •26.2.А лан Тьюринг
- •26.3.Джон Маулчи и Джон Эккерт
- •26.4.Джон фон Нейман
- •26.5.А ксель Берг
- •26.6.В иктор Глушков
- •26.7.Сергей Лебедев
- •26.8.Исаак Брук
- •26.9.Николай Матюхин
- •26.10.Михаил Карцев
- •26.11.Юрий Базилевский
- •26.12. Башир Рамеев
- •26.13.Георгий Лопато
- •26.14. Всеволод Бурцев
- •27.Приложения
- •27.1.Основные черты кибернетики
- •27.1.1.Общенаучное значение кибернетики
- •27.1.2.Электронные счетные машины и нервная система
- •27.1.3.Прикладное значение кибернетики
- •27.2."Сигнал" Игоря Полетаева
- •27.3.Хронология компьютеростроения
- •Литература
- •Оглавление
7.3.Элементарная алгебра, аналитические и численные вычисления
Если область допустимых значений каждого аргумента функции совпадает с областью ее значений, такую функцию принято называть операцией. Следовательно, базисные математические функции, из которых конструируются элементарные функции – суть операции.
В самом общем виде алгебра определяется как некоторое множество (носитель) на котором задана сигнатура операций. Мы будем говорить об элементарной алгебре, носителем которой является континуум вещественных чисел, а сигнатура состоит из базисных вещественных функций.
Выражение элементарной алгебры состоит из операндов и операций, записанных в соответствии с общеизвестными синтаксическими правилами. В программировании такое выражение называется арифметическим выражением. Существует три различных формата записи арифметического выражения: префиксный (знак операции ставится перед операндами этой операции), инфиксный (знак операции ставится между операндами этой операции) и постфиксный (знак операции ставится после операндов этой операции). Очевидно, что префиксный формат записи арифметического выражения является ничем иным как записью суперпозиции, определяющей элементарную функцию. Учитывая, что одно и то же арифметическое выражение может быть записано как в префиксном, так и в инфиксном формате, получаем, например:
f(x1,x2,x3,x4) = f*(f+(x1,x2),f-(x3,x4)) = (x1+x2)*(x3-x4) (34)
Аналитическая запись элементарной функции имеет следующий вид:
y = f*(x1,x2,…,xn) (35)
Здесь, f*(x1,x2,…,xn) – инфиксное арифметическое выражение, определяющее элементарную функцию f(x1,x2,…,xn).
Арифметическое выражение f*(x1,x2,…,xn) является именем значения функции, переменная y – второе имя функции. Запись (35) является утверждением: имя y и имя f#(x1,x2,…,xn) обозначают одно и то же значение функции (Рис.20).
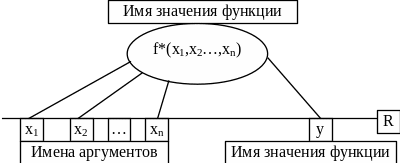
Рис. 20. Аналитический формат записи элементарной функции y = f(x1,x2,…,xn)
Вычисление - математическое преобразование, позволяющее преобразовывать набор исходных данных в выходной набор данных по вполне определенным правилам. Если смотреть с точки зрения теории информации, вычисление - это получение из входных данных нового знания. Вычисления подразделяются на аналитические и численные.
Аналитические вычисления преследуют цель преобразования исходных символьных строк в результирующие формулы, представленные в аналитическом виде. Такие преобразования реализуют упрощение арифметических выражений (приведение подобных, раскрытие скобок, группировку подобных членов); вычисление производных и интегралов; решение систем алгебраических и дифференциальных уравнений и т.д.
Аналитическое вычисление позволяет представить функциональную зависимость в общем виде для всего диапазона области допустимых значений функции. Это представление являет собой явную аналитическую формулу вида: y = f#(x1,…,xn). В случае, когда необходимо определить значение функции при заданных значениях ее аргументов: [x1],…,[xn], реализуется вычисление арифметического выражения f#(x1,…,xn) в два этапа:
конкретизация арифметического выражения - имена аргументов заменяются на значения аргументов;
вычисление конкретизации арифметического выражения посредством выполнения образующих его операций при заданных значениях операндов.
Пример. (x1+x2)*(x3-x4)/5,3,7,5 = (5+3)*(7-5) = 16
Примечание. Здесь особо проявляется целесообразность представления элементарной функции в виде арифметического выражения. Алгоритм вычисления любой конкретизации арифметического выражения существует и хорошо известен.
Мы рассмотрели случай, когда после аналитических вычислений полученный результат служит исходными данными для численных алгебраических вычислений. При этом численные вычисления сводятся, в конечном итоге, к выполнению в определенном порядке последовательности арифметических операций.
Однако, аналитические вычисления не всемогущи. Далеко не всегда при решении уравнений результат может быть представлен в аналитическом виде (в формате явной формулы элементарной функции). Вследствие этого невозможно вычислить значение функции при заданных аргументах посредством обозначения этого значения арифметическим выражением (Рис. 20) с последующей его конкретизацией.
Прежде всего подобная ситуация возникает при решении систем дифференциальных уравнений. В этом случае вычисление реализуется посредством выполнения специфического для данной системы уравнений алгоритма преобразующего значения аргументов функции (значения переменных и параметров уравнений) в численный результат, представляющий значение функции, т.е. решение системы уравнений в заданной точке. Подобную методологию принято называть численными алгоритмическими вычислениями.
Пример. Решение системы линейных дифференциальных уравнений методом Рунге – Кута.
