6.7.Вещественные числа

Дискретное множество натуральных чисел и дискретное множество целых чисел абстрагируют количественные (дискретные) характеристики реальных множеств (количество яблок в той или иной корзине) и отношения между этими характеристиками (насколько количество яблок в корзине A больше/меньше количества яблок в корзине B).

Вещественное, или действительное число  — математическая абстракция, возникшая из потребности представления непрерывных характеристик. Непрерывная характеристика может принимать любое значение из непрерывного множества. Например, температура объекта, сила тока в проводнике и т.д. и т.п. Для представления значений непрерывных характеристик используется множество записей вещественных чисел. Следовательно, прототипом вещественного числа должно служить непрерывное множество.

Неотрицательное вещественное число мы определим как функцию, отображающую непрерывное множество точек геометрического положительного луча L⁺ с началом O (прототип вещественного числа) в непрерывное множество записей неотрицательных вещественных чисел ⁺ - обозначений точек этого луча:

real⁺: L⁺⁺ (26)

Функция реализуется посредством измерения расстояния точки p L⁺ от начала O положительного луча и обозначения этого расстояния записью вещественного числа.

Пусть p – точка на L⁺ (Рис.15). Расстояние точки p от начала луча O равно (Рис.15):

([p]) = S_e([O,p¹]) + S_0.1e([p¹,p²]) + S_0.01e([p²,p]) (27)

Здесь, S_e([O,p¹]) – мерная последовательность с эталоном e, S_0.1e([p1,p²]) - мерная последовательность с эталоном , S_0.01e([p²,p]) - мерная последовательность с эталоном .

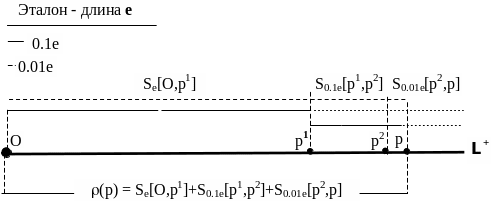
Рис. 15. Положительная вещественная числовая прямая как график функции real⁺ определения вещественного неотрицательного числа.

Для примера (Рис.15) мощности отрезков, образующих мерные последовательности равны: num((S_e([O,p¹]))) = 2, num((S_0.1e(p¹,p²])) = 5, num((S_0.01e(p²,p])) = 3. Следовательно, формула неотрицательного вещественного числа, обозначающего точку p имеет вид:

(28)

При e=1 запись этого числа в виде десятичной дроби имеет вид:

(29)

В общем случае, сумма мерных последовательностей бесконечна конечна, и формула неотрицательного вещественного числа имеет вид:

Здесь, d_i – цифра десятичной позиционной системы счисления.

Существенно, что любо

Соответствующая запись вещественного числа в виде десятичной дроби имеет вид:

…d_n-1…d₁d₀.d_-1d_-2… (30)

Здесь, d_i – цифра десятичной позиционной системы системы, точка отделяет целую часть числа от его дробной части.

Точка отделяет целую часть записи числа от дробной части. Если десятичная дробь конечна или периодична, то число определяется как действительное вещественное число. В противном случае, число – иррациональное вещественное число.

Аналогично предыдущему, множество ⁺ записей неотрицательных вещественных чисел расширяется до множества  записей вещественных чисел. В результате получается числовая прямая, которая является графиком функции real, определяющей вещественное число (Рис.16).

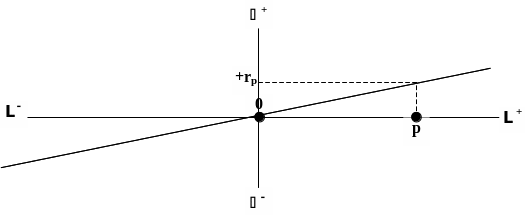
Рис. 16. Числовая прямая – как график функции real определения вещественного числа.

Алгебра вещественных чисел определяется следующим образом:

A_real = <;+,,,\> (31)

Здесь,  - множество записей вещественных чисел; +,,,\ - сигнатуры операций, относительно которых множество  замкнуто.

Измерительная шкала – функция (), отображающая какой либо атрибут таксона физических сущностей в множество записей вещественных чисел. Например, шкала температур:

scale^t: T (32)

Конструктивно, график функции () - реализуется в конструкции измерительного прибора в виде шкалы измерительного прибора, например – шкалы термометра. Шкала термометра – физическая линейка, размеченная значениями температуры, являет собой реализацию числовой прямой (Рис.17).

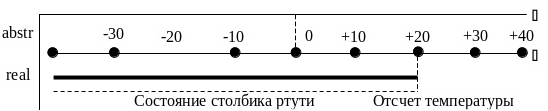
Рис. 17. Измерительная шкала термометра

Точки физической линейки :

• соответствуют точкам отрезка геометрической прямой L;

• представляют подмножество  непрерывного множества возможных значений температуры (функция abstr);

• являются аргументами функции real (), т.е. точкам на физической линейке  соответствуют записи вещественных чисел из .

Кроме шкалы в измерительный прибор входит датчик, состояния которого представляют возможные значения измеряемой характеристики. В случае термометра, датчиком является столбик ртути, длина которого "следит" за температурой внешней среды. Подразумевается, что в каждый момент времени длина столбика ртути (текущее состояние датчика) отражает текущее значение t температуры внешней среды. Текущее состояние датчика указывает вполне определенную точку на физической линейке термометра, что позволяет произвести отсчет текущей температуры внешней среды (т.е. вычислить значение функции realabsr в точке t).

Измерительная температурная шкала в совокупности с датчиком температуры (ртутным столбиком) образуют ртутный термометр.

Проблемой является определение реперных точек измерительной шкалы, т.е. значения измеряемой величины, которая считывается как запись "0" на измерительной шкале, и эталона измерения. Применительно к измерению температуры, исторически, "волевым решением" определены три измерительные шкалы температуры.

Интервальная шкала температуры Цельсия: 0С на температурной шкале соответствует температуре замерзания воды при атмосферном давлении в 1 атмосферу. Температура кипения воды - 100С на температурной шкале. Эталон измерения температуры – градус Цельсия: 1С = (t замерзания воды – t кипения воды)/100. Шкала предложена шведским ученым Андерсом Цельсием в 1742 г.

Относительная шкала температуры Фаренгейта: 0F – температура смеси воды, льда и нашатыря, 96F – температура тела здорового человека, 32F – точка таяния льда. Эталон измерения температуры – градус Фаренгейта: 1F = (t тела здорового человека –t смеси воды, льда и нашатыря)/100 = (t кипения воды – t таяния льда)/180. tC = 5/9(tF-32). Шкала предложена немецким ученым Габриэлем Фаренгейтом в 1724 г.

Абсолютная шкала температуры Кельвина. Абсолютный ноль – наиболее низкая возможная температура, при которой невозможно извлечь из вещества тепловую энергию.

Абсолютный ноль (0K) равен -273.15С. Точка замерзания воды: 273.16K. Эталон измерения температуры – градус Кельвина: 1K =1С. tС = tK-273.15. Шкала предложена британским физиком Уильямом Томcоном в 1848 году, которому было пожаловано звание лорд Кельвин.

Примечание. В настоящее время реперные точки шкалы Кельвина и шкалы Фаренгейта несколько изменены, что не вызывает большой разницы в "старых" и "новых" измерениях.

Хронология событий. Математик аль-Хорезми (около 820 г.), автор фундаментальной книги «Китаб Аль-джебр валь-мукабала» (от названия которой возникло слово «алгебра»), ввел понятие алгоритма, он же предложил десятичную систему счисления. Около 850 г. н. э. Аль-Хорезми публикует свой труд Арифметика.

В Европе ширится распространение арабских цифр, а также понятий нуль и позиционность. Постепенно арабские цифры вытесняют римские, но окончательно это произойдет лишь в XVII веке.

Итальянский математик, монах Лука Пачиоли (1445-1517) напечатал две книги: «Сумма знаний по арифметике, геометрии, учение о пропорции и пропорциональном», в которой впервые описываются письменные приемы счета и используются арабские цифры, и «Трактат о счетах и записях» – самую первую книгу по бухалтерскому учету. В ней впервые сформулирован основной принцип бухгалтерии – принцип двойной записи.

Леонтий Магницкий (1669—1739 гг.) — математик, преподаватель Московской навигационной школы, публикует книгу «Арифметика» — первое в России полноценное введение в математику. В ней впервые в России используется европейское десятичное исчисление. В последующие 50 лет «Арифметика» оставалась основным Российским математическим трудом.