
Проверка адекватности модели
Число степеней свободы дисперсии адекватности и воспроизводимости:

Пусть - значение функции y, предсказываемое уравнением регрессии.
|
|
|
|
|
0,9555 |
0,956125 |
3,90625E-07 |
2,25E-06 |
2,25E-06 |
0,9585 |
0,957875 |
3,90625E-07 |
2,5E-07 |
2,5E-07 |
0,964 |
0,963375 |
3,90625E-07 |
0,000001 |
0,000001 |
0,9665 |
0,967125 |
3,90625E-07 |
2,5E-07 |
2,5E-07 |
0,97 |
0,969375 |
3,90625E-07 |
0,000001 |
0,000001 |
0,974 |
0,974625 |
3,90625E-07 |
0,000001 |
0,000001 |
0,9775 |
0,978125 |
3,90625E-07 |
2,25E-06 |
2,25E-06 |
0,986 |
0,985375 |
3,90625E-07 |
0,000001 |
0,000001 |
|
|
3,125E-06 |
9E-06 |
9E-06 |

Экспериментальное значение критерия Фишера:
 .
.
Теоретическое значение критерия Фишера:
 .
.
S2aд |
S2y |
Fexp |
Ft |
1,5625E-06 |
2,25Е-06 |
0,6944 |
3,838 |
Поскольку , то модель адекватна.
Проверка значимости коэффициентов
Дисперсия оценок коэффициентов:

Теоретическое
значение критерия Стьюдента:
 .
.
Значения оценок критерия Стьюдента для коэффициентов:
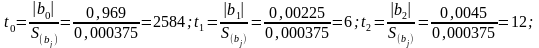

S(bj) |
t0 |
t1 |
t2 |
t3 |
t4 |
t5 |
t6 |
0,000375 |
2584 |
6 |
12 |
20,99 |
1,333 |
1 |
2,333 |
|
значим |
значим |
значим |
значим |
не значим |
не значим |
значим |
Уравнение регрессии в размерном виде:

