Тема 4. Введение в анализ
Тест 1. Общий член последовательности
равен:
а)
б)
в)
г)
Тест 2. Общий член последовательности
равен:
а)
б)
в)
г)
Тест 3. Сумма числового ряда
равна:
а) 2; б) 1; в) 1/16; г) 2/3.
Тест 4. Сумма числового ряда
равна:
а) 5/6; б) 1/216; в) 6/5; г) 1/5.
Тест 5. Образом отрезка [0; 3] является:
а) [1; 15]; б) [1; 6]; в) [6; 16]; г) [1; 16];
Тест 6. Если формула n-го
члена числовой последовательности
имеет вид
,
то
равно: а) 5/19; б) 3/14; в) 4/19; г) 1/4.
Тест 7. Если
,
то числовой ряд сходится при l,
равном:
а) -2,1; б) 2,1; в) 1,3; г) 0,3.
Тест 8. Для периодической функции
с периодом Т =12 при всех х из
области определения справедливо
равенство:
а)
б)
в)
г)
Тест 9. Периодической является функция:
а)
б)
в)
г)
Тест 10. Среди графиков, приведенных на рисунке, указать те из них, на которых функция имеет в точке а разрыв второго рода.
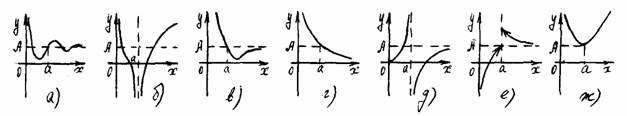
Тест 11. Значение функции
в
точке
можно вычислить по формуле:
а)
б)
в)
г)
Тест 12. Значение предела
равно:
а) 0; б) 4; в) ; г) 1
Тест 13. Значение предела
равно:
а) 4; б) 8; в) 2; г) 1.
Тест 14. Предел функции
равен:
а) 1; б) 0,5; в) 1,5; г) 0.
Тест 15. Предел функции
равен:
а) 1; б) 3; в) ; г) 0,5.
Ответы:1) в; 2) а; 3) а; 4) в; 5) г; 6) а; 7) г; 8) г; 9) г; 10) б и д; 11) г; 12) б; 13) а; 14) 0; 15) в.
Тема 5. Дифференциальное исчисление
Тест 1. Одно из нижеприведенных предложений определяет производную функции (при стремлении приращения аргумента к нулю):
а) Отношение приращения функции к приращению аргумента;
б) Отношение функции к пределу аргумента;
в) Отношение предела функции к аргументу;
г) Предел отношения приращения функции к приращению аргумента при стремлении последнего к нулю.
Тест 2. Первая производная функции показывает:
а) скорость изменения функции;
б) направление функции;
в) приращение функции;
г) приращение аргумента функции.
Тест 3. Угловой коэффициент касательной, проведенной к графику функции в некоторой точке, равен:
а) отношению значения функции к значению аргумента в этой точке;
б) значению производной функции в этой точке;
в) значению дифференциала функции в этой точке;
г) значению функции в этой точке;
Тест 4. Если функция дифференцируема в некоторой точке, то справедливо утверждение:
а) функция не определена;
б) нельзя провести касательную к графику функции;
в) функция непрерывна;
г) функция имеет экстремум.
Тест 5. Дифференциал функции равен:
а) отношению приращения функции к приращению аргумента;
б) произведению приращения функции на приращение аргумента;
в) произведению производной на приращение аргумента;
г) приращению функции.
Тест 6. Дифференциал постоянной равен:
а) этой постоянной;
б) произведению данной постоянной на величину Dx;
в) бесконечно большой величине;
г) нулю.
Тест 7. Для любой линейной функции верно следующее утверждение:
а) дифференциал функции равен приращению функции;
б) дифференциал функции равен приращению аргумента;
в) дифференциал функции – это постоянная величина;
г) дифференциал функции равен производной этой функции.
Тест 8. Если функция у(х) непрерывна на [a;b], дифференцируема на (a;b) и y(a) = y(b), то на (a;b) можно найти хотя бы одну точку, в которой:
а) функция не определена;
б) производная функции не существует;
в) нельзя провести касательную к графику функции;
г) производная функции обращается в ноль.
Тест 9. Какой из графиков на рисунке соответствует функции y = f(x), удовлетворяющей условиям f '(x) < 0; f ''(x) > 0?
Тест 10. Для дифференцируемой функции f(x) из приведенных условий выбрать достаточное условие убывания:
а) f’(x) > 0; б) f’(x) < 0; в) f’’(x) > 0; г) f’’(x) < 0; д) f’(x) = 0; е) f’’(x) = 0.
Тест 11. Для дифференцируемой функции f(x) из приведенных условий выберите достаточное условие выпуклости вверх:
а) f’(x) > 0; б) f’(x) < 0; в) f’’(x) > 0; г) f’’(x) < 0; д) f’(x) = 0; е) f’’(x) = 0.
Тест 12. Производная функции 
равна:
а)
б)
в)
г)
Тест 13. График функции кривая y = ln(x) пересекает ось ОХ под углом, равным:
а) /6; б) p/4; в) p/3; г) p/8.
.
Тест 14. График функции изображен на рисунке:
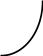
y
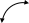
1200 x0
x
Значение производной этой функции в точке х0 равно:
а)
б)
в)
г)
Тест 15. Производная функции
равна:
а)
б)
в)
г)
Ответы: 1) г; 2) а; 3) б; 4) в; 5) в; 6) г; 7) а; 8) г; 9) б; 10) б; 11) г; 12) а; 13) б; 14) в; 15) г.