
- •Математика
- •4. Содержание разделов и тем дисциплины
- •Раздел I. Аналитическая геометрия и линейная алгебра
- •Тема 1. Элементы аналитической геометрии и векторный анализ
- •Тема 2. Основы теории матриц
- •Раздел II. Математический анализ
- •Тема 3. Введение в анализ
- •Тема 4. Дифференциальное исчисление
- •Тема 5. Интегральное исчисление и дифференциальные
- •Раздел III. Теория вероятностей и математическая статистика
- •Тема 6. Основные понятия и основные законы теории
- •Тема 7. Случайные величины и система случайных величин
- •Тема 8. Основы математической статистики
- •5. Учебно-методическое обеспечение дисциплины
- •1. Вопросы к экзамену и зачету
- •2. Темы рефератов
- •3. Основная литература
- •4. Дополнительная литература:
- •Теоретические вопросы для выполнения контрольной работы
- •Контрольные вопросы для самостоятельной работы студентов
- •Тестовые задания
- •Тема 1. Элементы аналитической геометрии и векторный анализ
- •Тема 2. Основы теории матриц
- •Тема 3. Прикладные методы и модели линейной алгебры
- •Тема 4. Введение в анализ
- •Тема 5. Дифференциальное исчисление
- •Тема 6. Интегральное исчисление и дифференциальные уравнения
- •Тема 7. Математические методы и модели социально-экономических процессов
- •Тема 8. Основные понятия и основные законы теории вероятностей
- •Тема 9. Случайные величины и система случайных величин
- •Тема 10. Основы математической статистики
- •Тема 11. Прикладные методы теории вероятностей и математической статистики
- •Словарь основных терминов
Тестовые задания
Тема 1. Элементы аналитической геометрии и векторный анализ
Тест 1. Векторы А = (-1; 3; 2) и В = (k; 9; 6) коллинеарны, если k равно:
а) 3; б) -3; в) 1; г) -1.
Тест 2. Длина отрезка, отсекаемого прямой 4x + 2y -24 = 0 на оси Ox, равна:
а) 24; б) 5; в) 7; г) 6.
Тест 3. Модуль комплексного числа 8 -6i равен:
а) 3; б) 10; в) 14; г) 6.
Тест 4. Модуль комплексного числа 9 + 12i равен:
а) 9; б) 15; в) 12; г) 21.
Тест 5. Угловой коэффициент прямой 12x + 3y - 11 = 0 равен:
а) 3; б) -12; в) -4; г) 4.
Тест 6. Угловой коэффициент прямой 28x + 7y - 4 = 0 равен:
а) -4; б) -28; в) 7; г) 4.
Тест 7. Угловой коэффициент прямой 6x + 3y - 7 = 0 равен:
а) 2; б) -2; в) -6; г) 3.
Тест 8. Нормальный вектор плоскости x – y -11z -1 = 0 имеет координаты:
а) -1; -11; -1; б) -1; 1; 11; в) 1; -1; -11; г) 1; 11;1.
Тест 9. Норма вектора А = 10i – 10j + 5k в пространстве R3 равна:
а) 225; б) -15; в) 15; г) 25.
Тест 10. Если скалярное произведение
векторов
![]() и
и
![]() равно
равно
![]() ,
а модули этих векторов равны
,
а модули этих векторов равны
![]() и
и
![]() ,
то угол между векторами
и
равен:
,
то угол между векторами
и
равен:
а) /4; б) 3/4; в) /6; г) .
Тест 11. Аргумент комплексного числа
![]() равен:
равен:
а) 4/3; б) /3; в) 7/6; г) /6.
Тест 12. Прямая линия проходит через точки А(0; 0) и В(15; 3). Тогда ее угловой коэффициент равен:
а) -5; б) 5; в) 1/5; г) –1/5.
Тест 13. Расстояние между точками А(-1; 1) и В(k; -3) равно 5 при k, равном:
а) 4; б) 8; в) -1; г) -4.
Тест 14. Скалярное произведение
векторов
![]() и
и
![]() равно:
равно:
а) 3; б) 4; в) -2; г) 0.
Тест 15. Вектор
![]() перпендикулярен вектору
перпендикулярен вектору
![]() ,
если величина
равна:
,
если величина
равна:
а) -1; б) 1; в) 0; г) 3.
Ответы: 1) в; 2) г; 3) б; 4) б; 5) в; 6) а; 7) б; 8) в; 9) в; 10) а; 11) а; 12) в; 13) -4; 14) б; 15) 1.
Тема 2. Основы теории матриц
Тест 1. При перестановке двух строк (столбцов) матрицы ее определитель:
а) изменяет знак на противоположный;
б) не изменяет знака;
в) становится равным нулю;
г) увеличивается вдвое.
Ответ: а).
Тест 2. Решение систем линейных уравнений методом Крамера предполагает:
а) вычисление только определителя матрицы системы;
б) вычисление нескольких определителей, число которых зависит от порядка системы;
в) последовательное исключение переменных;
г) вычисление ранга матрицы.
Тест 3. Умножение двух прямоугольных матриц можно осуществлять, если:
а) обязательно соблюдается равенство числа строк и столбцов обеих матриц;
б) число строк первой матрицы равно числу столбцов второй матрицы;
в) число столбцов первой матрицы равно числу строк второй матрицы;
г) обе матрицы имеют одинаковую структуру.
Тест
4. Определитель
![]() равен нулю, если
равен:
равен нулю, если
равен:
а) -6; б) 0; в) 2; г) -2.
Тест
5. Дана
матрица
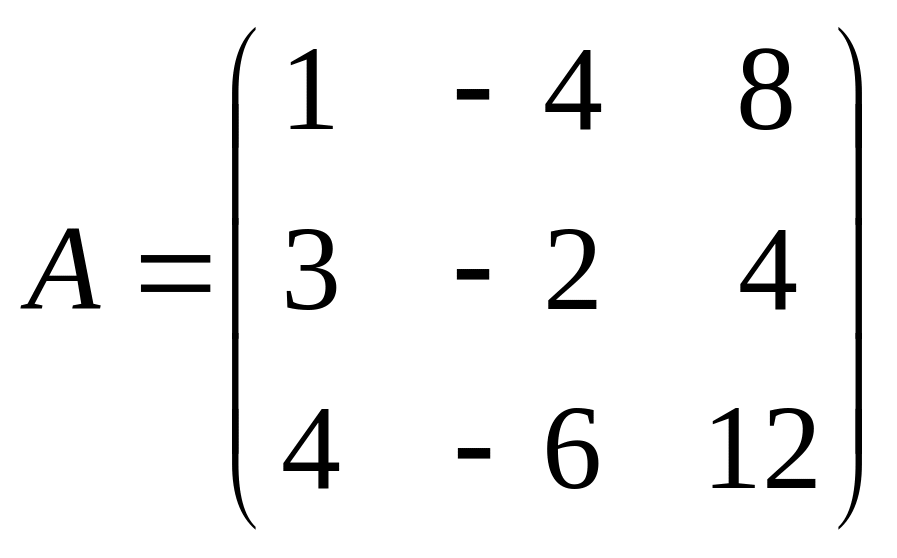 .
Для этой матрицы сумма элементов
.
Для этой матрицы сумма элементов
![]()
![]()
равна: а) 12; б) -12; в) 9; г) 10.
Тест 6. Даны матрицы
![]() и
и
![]() .
Их разность А – В равна:
.
Их разность А – В равна:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Тест 7. Определитель
![]() равен:
равен:
а) 22; б) -2; в) 2; г) 0.
Тест 8. Если
![]() ,
то матрица 5А имеет вид:
,
то матрица 5А имеет вид:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Тест 9. Определитель
![]() равен:
равен:
а) -7; б) 7; в) -1; г) 3.
Тест 10. Даны матрицы и . Их сумма А+ В равна:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Тест 11. Определитель
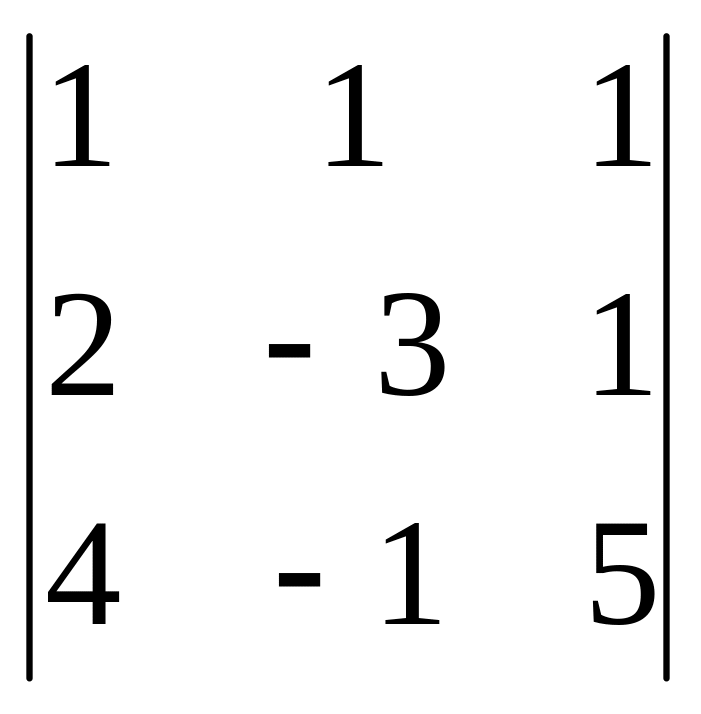 равен:
равен:
а) 15; б) 40; в) -20; г) 30.
Тест 12. Ранг матрицы
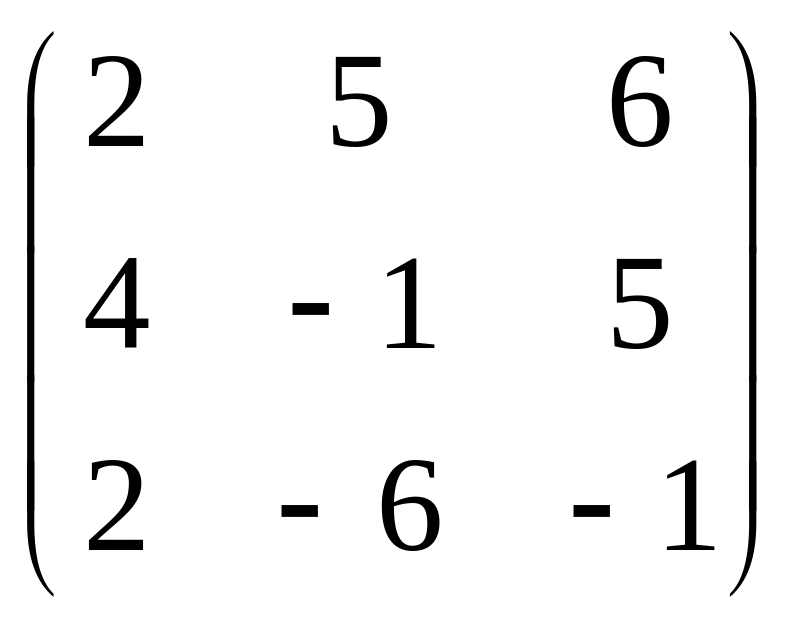 равен:
равен:
а) 3; б) 2; в) 0; г) 1.
Тест 13. Произведение матриц
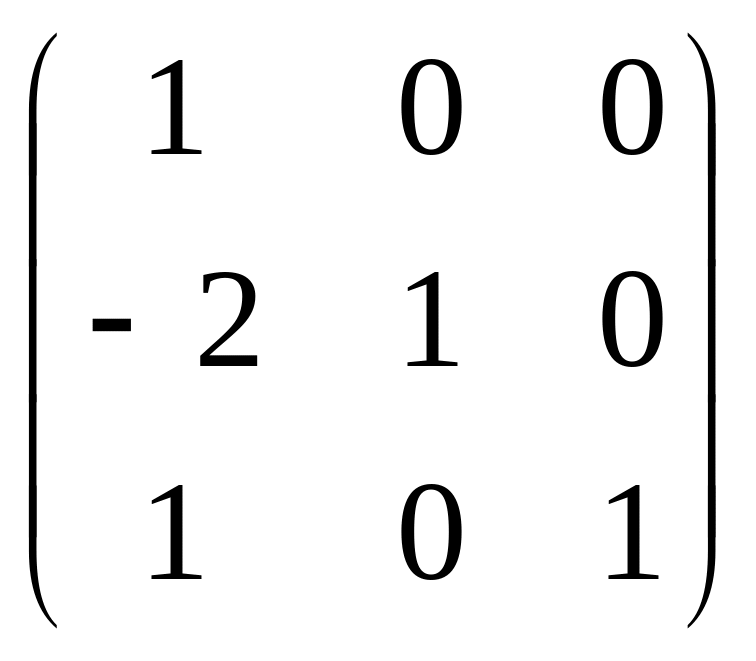 и
и
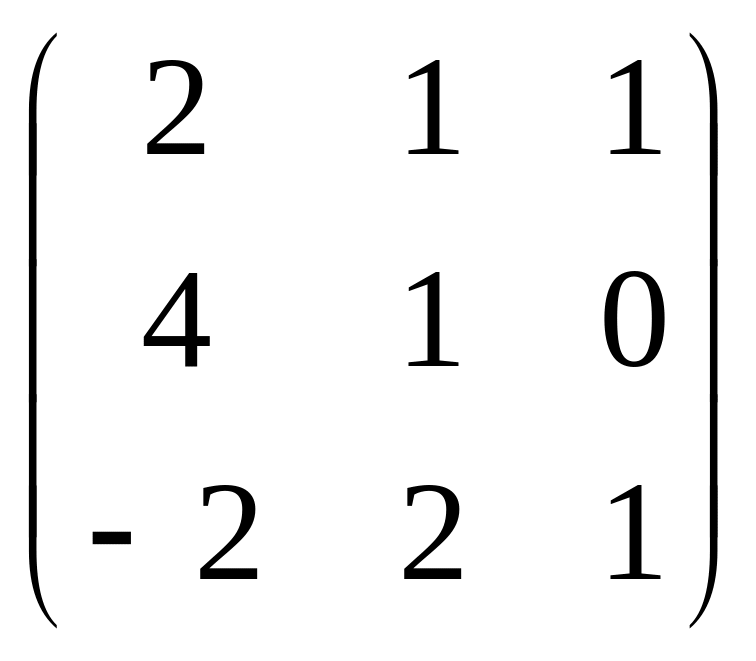 равно:
равно:
a)
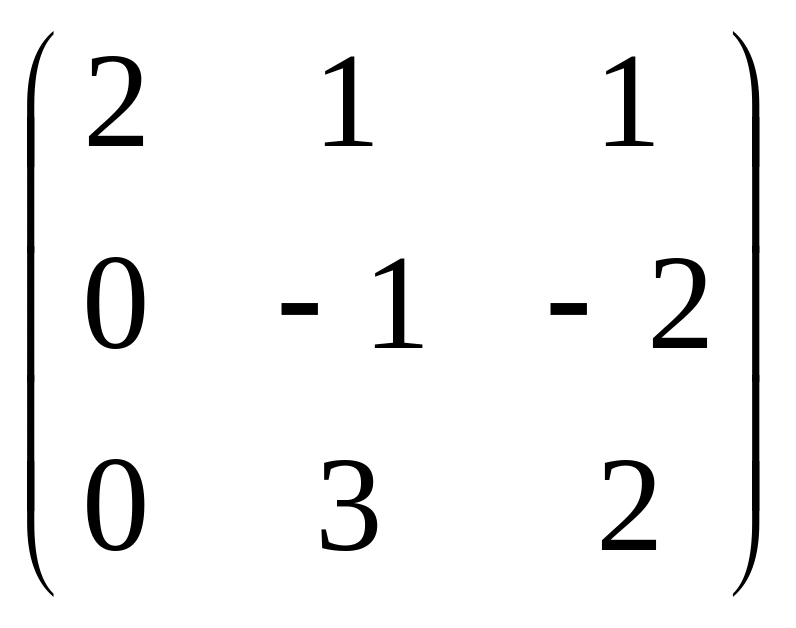 ;
б)
;
б)
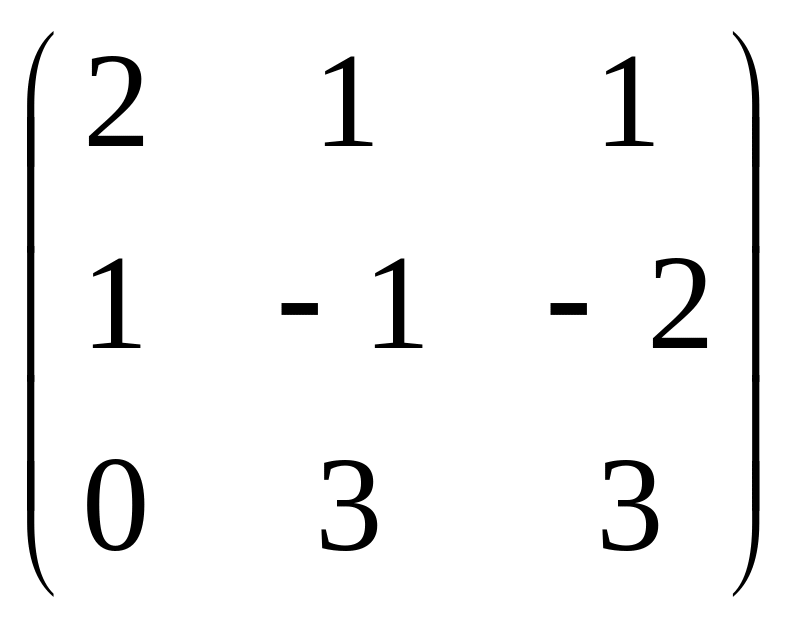 ;
в)
;
в)
 ;
г) 28.
;
г) 28.
Тест 14. Матрица, обратная матрице
![]() ,
равна:
,
равна:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Тест 15. Матрица, обратная матрице
![]() ,
равна:
,
равна:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ; г)
; г)
![]() .
.
Ответы: 1) а; 2) б; 3) в; 4) в; 5) г; 6) б; 7) б; 8) г; 9) а; 10) а; 11) б; 12) б; 13) а; 14) в; 15) б.
