
- •Математика
- •4. Содержание разделов и тем дисциплины
- •Раздел I. Аналитическая геометрия и линейная алгебра
- •Тема 1. Элементы аналитической геометрии и векторный анализ
- •Тема 2. Основы теории матриц
- •Раздел II. Математический анализ
- •Тема 3. Введение в анализ
- •Тема 4. Дифференциальное исчисление
- •Тема 5. Интегральное исчисление и дифференциальные
- •Раздел III. Теория вероятностей и математическая статистика
- •Тема 6. Основные понятия и основные законы теории
- •Тема 7. Случайные величины и система случайных величин
- •Тема 8. Основы математической статистики
- •5. Учебно-методическое обеспечение дисциплины
- •1. Вопросы к экзамену и зачету
- •2. Темы рефератов
- •3. Основная литература
- •4. Дополнительная литература:
- •Теоретические вопросы для выполнения контрольной работы
- •Контрольные вопросы для самостоятельной работы студентов
- •Тестовые задания
- •Тема 1. Элементы аналитической геометрии и векторный анализ
- •Тема 2. Основы теории матриц
- •Тема 3. Прикладные методы и модели линейной алгебры
- •Тема 4. Введение в анализ
- •Тема 5. Дифференциальное исчисление
- •Тема 6. Интегральное исчисление и дифференциальные уравнения
- •Тема 7. Математические методы и модели социально-экономических процессов
- •Тема 8. Основные понятия и основные законы теории вероятностей
- •Тема 9. Случайные величины и система случайных величин
- •Тема 10. Основы математической статистики
- •Тема 11. Прикладные методы теории вероятностей и математической статистики
- •Словарь основных терминов
Тема 10. Основы математической статистики
Тест 1. К основным задачам математической статистики относится:
а) статистическая проверка гипотез;
б) вычисление вероятности случайного события;
в) расчет числовых характеристик теоретических распределений вероятностей;
г) анализ преобразований случайных величин.
Тест 2. Характеристикой оценок числовых характеристик по результатам выборочных значений является:
а) репрезентативность оценки;
б) несмещенность оценки;
в) сходимость любой оценки к математическому ожиданию теоретического распределения;
г) независимость оценки от объема выборки.
Тест 3. В результате 10 опытов получены следующие выборочные значения: 3; 3; 4; 4; 4; 5; 5; 5; 6; 6. Законом распределения для выборки является:
а) |
xi |
1 |
2 |
3 |
4 |
б) |
xi |
3 |
4 |
5 |
6 |
pi |
0,2 |
0,3 |
0,3 |
0,2 |
pi |
0,4 |
0,6 |
0,6 |
0,4 |
в) |
xi |
3 |
4 |
5 |
6 |
г) |
xi |
3 |
4 |
5 |
6 |
pi |
0,2 |
0,3 |
0,3 |
0,2 |
pi |
0,2 |
0,4 |
0,3 |
0,2 |
Тест 4. В результате 10 опытов получены следующие выборочные значения: 2; 3; 3; 4; 4; 4; 4; 5; 5; 5. Законом распределения для выборки является:
а) |
xi |
2 |
3 |
4 |
5 |
б) |
xi |
1 |
2 |
3 |
4 |
pi |
0,1 |
0,2 |
0,4 |
0,3 |
pi |
0,1 |
0,2 |
0,4 |
0,3 |
в) |
xi |
2 |
3 |
4 |
5 |
г) |
xi |
2 |
3 |
4 |
5 |
pi |
0,2 |
0,4 |
0,8 |
0,6 |
pi |
0,1 |
0,3 |
0,4 |
0,3 |
Тест 5. В результате измерений некоторой физической величины одним прибором (без систематических ошибок) получены следующие результаты: 10, 13, 13. Тогда несмещенная оценка дисперсии измерений равна:
а) 6; б) 2; в) 12; г) 3.
Тест 6. Из генеральной совокупности извлечена выборка объемом n = 49, полигон частот которой имеет вид:
ni

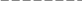

 20
20


 16
16



 3
3

0 1 2 3 4 xi
Тогда число выборочных значений (число
вариант) для
![]() равно:
равно:
а) 11; б) 9; в) 10; г) 49.
Тест 7. По формуле для оценки средней
величины выборочного распределения (n
– объем выборки, xi
– выборочные значения) вида
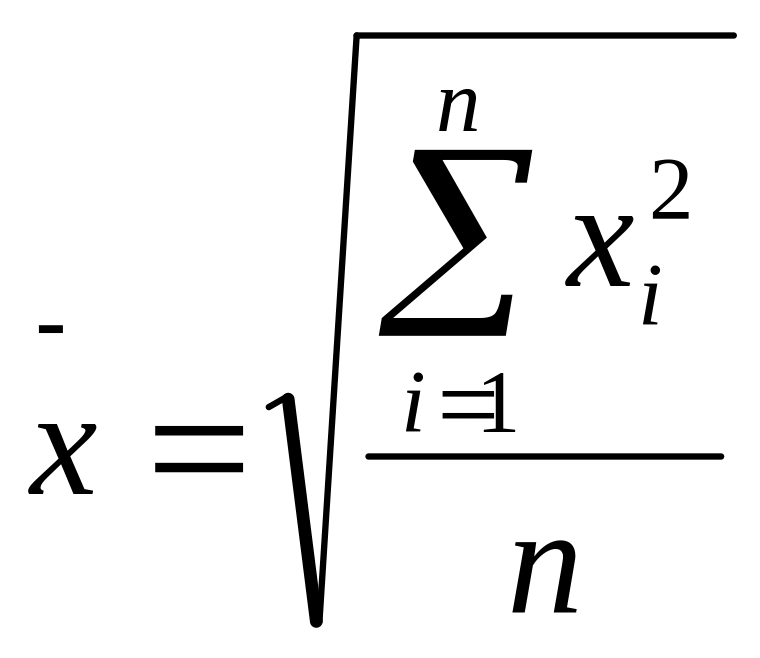 рассчитывается:
рассчитывается:
а) средняя арифметическая;
б) средняя геометрическая;
в) средняя геометрическая;
г) средняя квадратическая.
Тест 8. Для расчета средней арифметической статистической совокупности используется формула (n – объем выборки, xi – выборочные значения):
а)
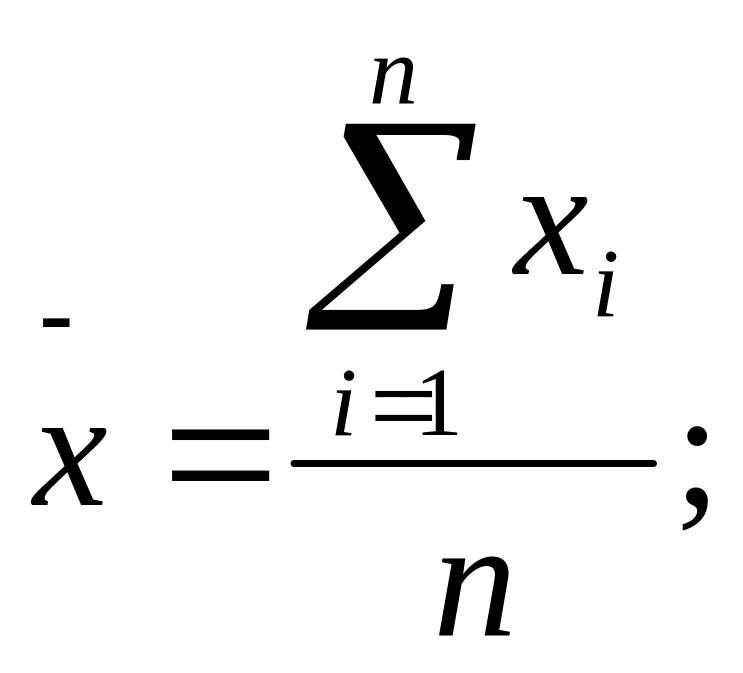 б)
б)
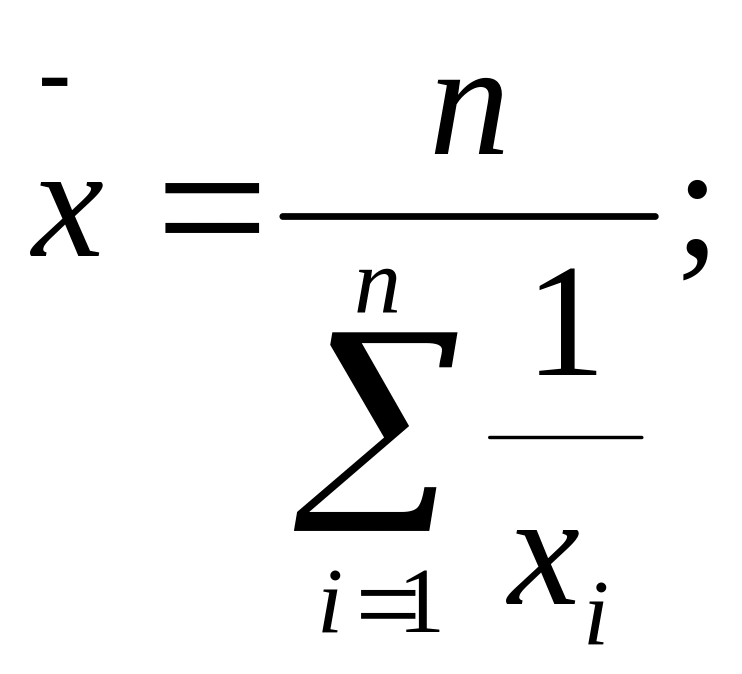 в)
в)
![]() г)
г)

Тест 9. Наиболее часто встречающееся значение признака у единиц данной статистической совокупности – это:
а) среднее линейное отклонение;
б) мода;
в) медиана;
г) среднее квадратическое отклонение.
Тест 10. Выборка задана в виде распределения частот (xi – выборочные значения; ni - соответствующие частоты):
xi |
4 |
7 |
8 |
12 |
17 |
ni |
2 |
4 |
5 |
6 |
3 |
Распределение относительных частот wi имеет вид:
а) |
xi |
4 |
7 |
8 |
12 |
17 |
б) |
xi |
4 |
7 |
8 |
12 |
17 |
wi |
0,1 |
0,2 |
0,25 |
0,3 |
0,15 |
wi |
0,1 |
0,2 |
0,3 |
0,2 |
0,2 |
в) |
xi |
4 |
7 |
8 |
12 |
17 |
г) |
xi |
4 |
7 |
8 |
12 |
17 |
wi |
0,2 |
0,2 |
0,2 |
0,2 |
0,2 |
wi |
0,2 |
0,1 |
0,3 |
0,3 |
0,1 |
Тест 11. Показателем вариации признака статистической совокупности является:
а) мода; б) медиана; в) относительная частота; г) дисперсия.
Тест 12. Формула Стерджесса для определения оптимального числа групп k при группировке данных статистической совокупности имеет вид (N – число единиц в совокупности):
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
Ответы: 1) в; 2) б; 3) в; 4) а; 5) б; 6) в; 7) г; 8) а; 9) б; 10) а; 11) г; 12) в.
