
- •Математика
- •4. Содержание разделов и тем дисциплины
- •Раздел I. Аналитическая геометрия и линейная алгебра
- •Тема 1. Элементы аналитической геометрии и векторный анализ
- •Тема 2. Основы теории матриц
- •Раздел II. Математический анализ
- •Тема 3. Введение в анализ
- •Тема 4. Дифференциальное исчисление
- •Тема 5. Интегральное исчисление и дифференциальные
- •Раздел III. Теория вероятностей и математическая статистика
- •Тема 6. Основные понятия и основные законы теории
- •Тема 7. Случайные величины и система случайных величин
- •Тема 8. Основы математической статистики
- •5. Учебно-методическое обеспечение дисциплины
- •1. Вопросы к экзамену и зачету
- •2. Темы рефератов
- •3. Основная литература
- •4. Дополнительная литература:
- •Теоретические вопросы для выполнения контрольной работы
- •Контрольные вопросы для самостоятельной работы студентов
- •Тестовые задания
- •Тема 1. Элементы аналитической геометрии и векторный анализ
- •Тема 2. Основы теории матриц
- •Тема 3. Прикладные методы и модели линейной алгебры
- •Тема 4. Введение в анализ
- •Тема 5. Дифференциальное исчисление
- •Тема 6. Интегральное исчисление и дифференциальные уравнения
- •Тема 7. Математические методы и модели социально-экономических процессов
- •Тема 8. Основные понятия и основные законы теории вероятностей
- •Тема 9. Случайные величины и система случайных величин
- •Тема 10. Основы математической статистики
- •Тема 11. Прикладные методы теории вероятностей и математической статистики
- •Словарь основных терминов
Тема 9. Случайные величины и система случайных величин
Тест 1. Ряд распределения дискретной случайной величины характеризует:
а) только возможные значения случайной величины;
б) только вероятности значений случайной величины;
в) соответствие между значениями случайной величины и их вероятностями;
г) минимальное и максимальное значения случайной величины.
Тест 2. Функция распределения случайной величины определяется как:
а) вероятность попадания случайной величины в область правее (более) заданного значения;
б) вероятность попадания случайной величины в область левее (менее) заданного значения;
в) вероятность попадания случайной величины в заданный интервал;
г) диапазон изменения случайной величины.
Тест 3. На рисунке изображены четыре
кривые, характеризующие случайные
величины с гауссовскими плотностями
вероятности
![]() и
одинаковыми математическими ожиданиями,
равными m. Наибольшее
значение дисперсии соответствует
кривой:
и
одинаковыми математическими ожиданиями,
равными m. Наибольшее
значение дисперсии соответствует
кривой:
а) 1; б) 2; в) 3; г) 4.
р(х)
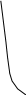 1
1

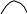 2
2

 3
3






 4
4
 m
х
m
х
Тест 4. Дисперсия случайной величины имеет размерность:
а) самой случайной величины;
б) квадрата случайной величины;
в) является безразмерной величиной;
г) обратную размерности случайной величины.
Тест 5. Дисперсия разности двух независимых случайных величин равна:
а) сумме дисперсий этих случайных величин;
б) разности дисперсий этих случайных величин;
в) разности квадратов математических ожиданий двух случайных величин;
г) произведению среднеквадратических отклонений двух случайных величин.
Тест 6. Дискретная случайная
величина
![]() имеет закон распределения:
имеет закон распределения:
-
X
2
4
7
11
P
0,1
0,2
P3
0,5
Вероятность
![]() равна:
равна:
а) 0,5; б) 0,25; в) 0,3; г) 0,2.
Тест 7. Математическое ожидание
![]() случайной
величины Y = 5X-3
при M(X) =
2 равно:
случайной
величины Y = 5X-3
при M(X) =
2 равно:
а) 5; б) 7; в) 10; г) 3.
Тест 8. Дискретная случайная величина Х имеет закон распределения вероятностей:
-
Х
2
4
P
0,2
0,8
Математическое ожидание M(X) этой случайной величины равно:
а) 6; б) 3,6; в) 1; г) 2,4.
Тест 9. Из изображенных на рисунке
кривых линий
![]() в
качестве функции распределения случайной
величины с математическими ожиданием
m может рассматриваться:
в
качестве функции распределения случайной
величины с математическими ожиданием
m может рассматриваться:
а) 1; б) 2; в) 3; г) 4.
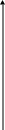
 F(x)
1
F(x)
1
 F(x)
= 1
F(x)
= 1



2

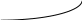
3
4

m x
Тест 10. Случайная величина равномерно распределена на интервале [0; 4]. Тогда ее плотность вероятности принимает значение, равное:
а)
![]() б)
б)
![]() в)
г) 4.
в)
г) 4.
Тест 11. Случайная величина равномерно распределена на интервале [a, b]. Тогда ее математическое ожидание равн:
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
Тест 12. Непрерывная случайная
величина X задана гауссовской
плотностью вероятности
![]() Тогда математическое ожидание этой
случайной величины равно:
Тогда математическое ожидание этой
случайной величины равно:
а) 100; б) 10; в) 200; г) 11.
Тест 13. Дисперсии двух независимых
случайных величин X
и Y равны:
![]()
![]() Тогда
дисперсия разности этих случайных
величин
Тогда
дисперсия разности этих случайных
величин
![]() равна:
равна:
а) 24; б) 36; в) 11; г) 12.
Тест 14. Дисперсия случайной величины
Х равна
![]() Тогда дисперсия случайной величины
Тогда дисперсия случайной величины
![]() равна: а) 36; б) 16; в) 1; г) 10.
равна: а) 36; б) 16; в) 1; г) 10.
Тест 15. Функция распределения F(x, y) системы двух случайных величин (X, Y) равна единице. Это равенство справедливо для следующей совокупности значений аргументов (x, y):
а)
![]() б)
б)
![]() в)
в)
![]() г)
г)
![]()
Ответы: 1) в; 2) б; 3) г; 4) б; 5) а; 6) г; 7) б; 8) б; 9) б; 10) а; 11) а; 12) г; 13) в; 14) а; 15) г
