Тема 8. Основные понятия и основные законы теории вероятностей

Тест 1. Несовместными являются следующие события:

а) появление герба и цифры при однократном подбрасывании одной монеты;

б) появление гербов на двух монетах при их однократном подбрасывании;

в) успешная сдача экзаменов студентом хотя бы по одному из двух предметов;

г) попадание в мишень одного или другого из стрелков.

Тест 2. Имеется 10 качественных и 4 бракованных изделий. Извлекается одно изделие. Событие А – “извлечено качественное изделие”, событие B – “извлечено бракованное изделие”. Для этих событий неверным является утверждение:

а) вероятность события В равна 2/7;

б) вероятность события А равна вероятности события В;

в) события А и В несовместны;

г) вероятность события А равна 5/7.

Тест 3. Вероятность наступления некоторого события не может быть равной:

а) 0,6; б) 1; в) 3; г) 0.

Тест 4. Вероятность наступления некоторого события не может быть равной:

а) 1; б) 0,4; в) 0; г) -1.

Тест 5. Игральный кубик подбрасывают один раз. Вероятность того, что на верхней грани выпадет число очков, равное двум или четырем, равна:

а) б) в) г)

Тест 6. Игральный кубик подбрасывают один раз. Событие А – “выпало число очков, большее трех”; событие В – “выпало число очков, меньшее трех”. Верным является утверждение:

а) события А и В совместны; б) события А и В несовместны;

в) событие В достоверно; г) событие А достоверно.

Тест 7. Количество комбинаций, которые можно получить путем перестановки букв, входящих в слово “число”, равно:

а) 24; б) 120; в) 80; г) 20.

Тест 8. Количество различных способов выбора (порядок не имеет значения) 3 томов из 8-томного собрания сочинений равно:

а) 11; б) 24; в) 56; г) 252.

Тест 9. Первый студент успешно ответит на данный вариант тестов с вероятностью 0,5, а второй – с вероятностью 0,7. Вероятность того, что оба студента успешно пройдут тестирование, равна:

а) 0,5; б) 0,7; в) 0,35; г) 0,1.

Тест 10. Вероятность для студента сдать первый экзамен равна 0,6, второй — 0,4. Вероятность сдать либо первый, либо второй, либо оба экзамена равна:

а) 0,24; б) 0,5; в) 0,6; г) 0,76.

Тест 11. Первый стрелок попадает в мишень с вероятностью 0,9, а второй – с вероятностью 0,5. Каждый стрелок делает по одному выстрелу. Вероятность того, что оба стрелка попадут в мишень, равна:

а) 1,4; б) 0,45; в) 1; г) 0,55.

Тест 12. В урне имеется а белых и b черных шаров. Из урны вынимают (одновременно или последовательно) два шара. Вероятность того, что оба шара окажутся белыми, равна:

а) б) в) г)

Тест 13. Вероятность попадания в мишень для 1-го стрелка составляет 0,8, для 2-го стрелка эта вероятность равна 0,7. Вероятность того, что в мишень попадет хотя бы один стрелок, равна:

а) 0,56; б) 0,75; в) 0,94; г) 0,5.

Тест 14. В партии из N изделий М изделий являются бракованными. Вероятность того, что при выборочном контроле из n выбранных изделий бракованными окажутся m изделий (m<n; С - символ числа сочетаний):

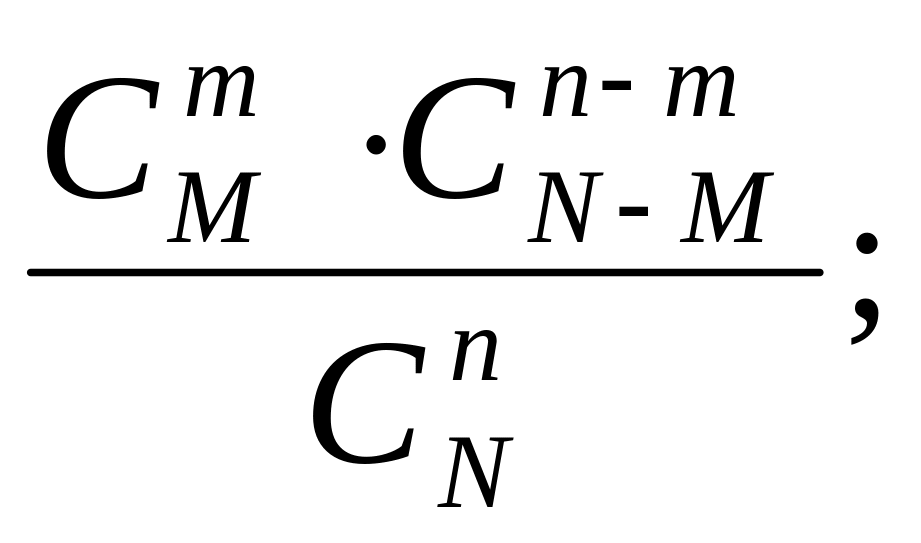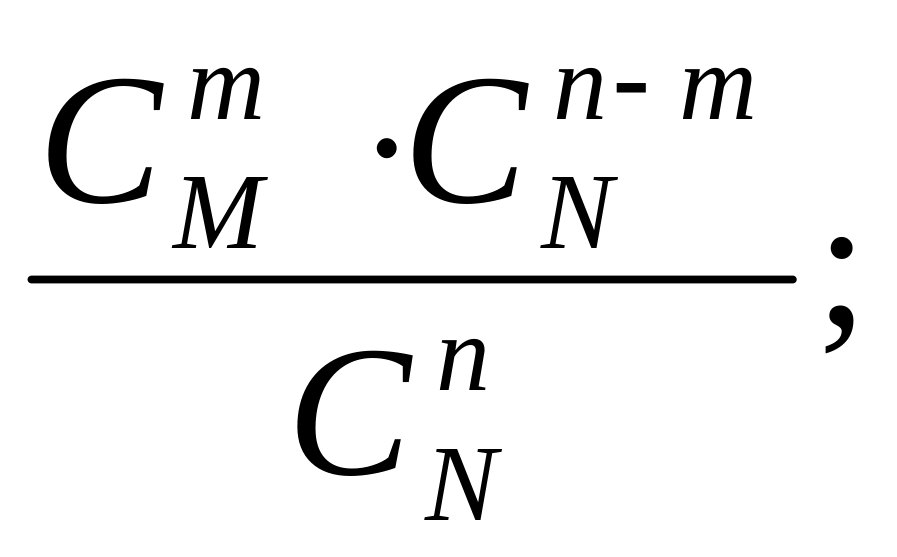а) б) в) г)

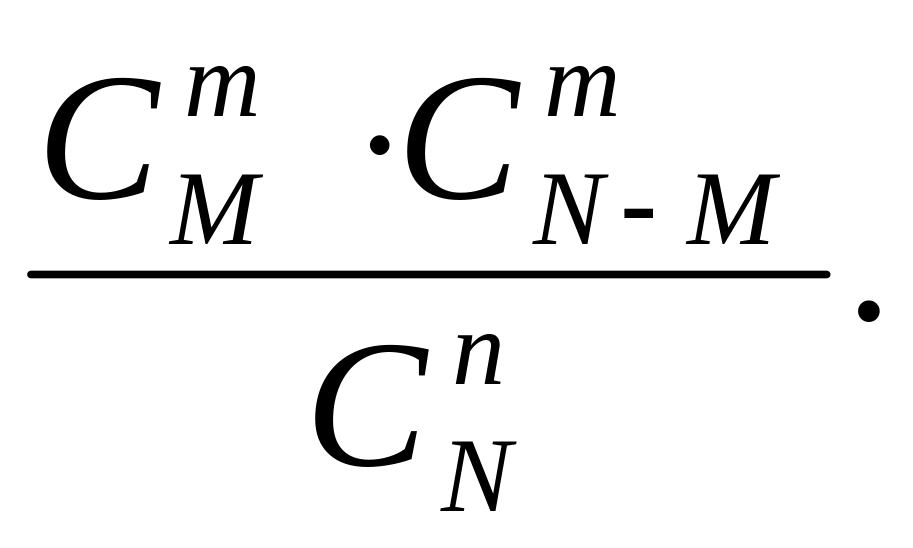
Тест 15. Абонент забыл две последних цифры телефонного номера и, зная, лишь, что они различны, набрал их наудачу. Число способов, которыми он это может сделать, равно:

а) 20; б) 90; в) 120; г) 75.

Тест 16. Заготовка может поступить для обработки на один из двух станков с вероятностями 0,7 и 0,3 соответственно. Вероятность брака для первого станка равна 0,3, для второго равна 0,1. Вероятность того, что наугад взятая деталь окажется бракованной, равна:

а) 0,5; б) 0,6; в) 0,35; г) 0,24.

Ответы: 1) а; 2) б; 3) в; 4) г; 5) а; 6) б; 7) б; 8) в; 9) в; 10) г; 11) б; 12) а; 13) в; 14) а; 15) б; 16) г.