Министерство по образованию РФ

Рязанский государственный радиотехнический университет

Кафедра АИТП

Курсовая работа по электронике на тему:

"Расчёт схем с операционными усилителями".

Выполнила студентка гр.638

Харламова Екатерина Игоревна

Проверил

Миловзоров Владимир Петрович

Рязань 2008г.

Содержание

Задание на курсовую работу………………………………………………………….3

1. Введение……………………………………………………………………………4

2. Расчет пропорционально-интегрального ПИ звена……………………………..5

3. Расчет пропорционально-дифференциального ПД звена………………………10

4. Расчет неинвертируемого усилителя переменного напряжения…....………….13

5. Расчет сравнивающего устройства……………………………………………….16

6. Заключение…………………………………………………………………………17

1. Введение.

Операционный усилитель – это усилительное устройство с большим коэффициентом усиления в широкой полосе частот, начиная с нулевой частоты. Он имеет очень высокий коэффициент усиления по напряжению, высокое входное и низкое выходное сопротивление, очень низкий входной ток – доли мкА и даже нА. Условное обозначение операционного усилителя:

Операционный усилитель, как правило, сложное многокаскадное электронное устройство, частично выполненное на дифференциальных усилительных каскадах.

Обычно операционный усилитель имеет две пары входных и одну пару выходных электродов. Вход, напряжение на котором совпадает по фазе с выходным напряжением, носит название неинвертирующий. Второй вход, напряжение на котором сдвинуто по фазе на 180° относительно выходного напряжения, носит название инвертирующего.

Характерной особенностью операционного усилителя является то, что он дает возможность получить близкое к нулю выходное напряжение при отсутствии входного сигнала. При этом потенциалы обоих входов будут близки к потенциалу выхода усилителя. Эти свойства операционного усилителя позволяют подключать нагрузку и источники входных напряжений, не заботясь о разделении переменной и постоянной составляющих. В составе операционного усилителя условно можно выделить входную, выходную части и каскады связи между ними. Входную часть операционного усилителя содержит дифференциальные усилители.

Выходная часть включает каскады усиления по мощности и обеспечивает работу операционного усилителя на заданную нагрузку с определенной амплитудой выходного напряжения. Каскады связи служат для усиления по напряжению, и позволяет осуществить согласование уровней сигнала.

Операционные усилители выполняются в виде монолитных интегральных микросхем и по своим размерам они почти не отличаются от отдельно взятого транзистора. Благодаря практически идеальным характеристикам операционных усилителей реализация схем на их основе оказывается значительно проще, чем на отдельных транзисторах.

2. Расчет пропорционально-интегрального пи звена.

Эта схема должна обеспечивать на выходе напряжение, связанное с входным выражением:

Начинать расчёт необходимо с определения минимально возможного значения сопротивления резистора R₁, которое обеспечивало бы выполнение условия (пункт 3 задания). Напомним, что пункт 3 требует, чтобы падение на внутренних сопротивлениях источника входного сигнала не превышало 0,85% .

Для входного сигнала можно записать:

, подставим это выражение в условие пункта 3:

;

.

Для ограничения ε можно найти минимально допустимое значение R₁(R_1min).

Сокращая на Е, получим:

;

, отсюда .

Так как Rвн=300 Ом, а ε = 0,85% = 0,0085, то получаем

R_1min=300 )≈34994,12Ом.

Продолжая расчет схемы ПИ звена, рассчитаем сопротивление R2 и емкость конденсатора С₁.

Обеспечение заданного α.

Так как , то .

Задано α=0,17, тогда R₂=0,17*34994,12≈5948,98 Ом

Обеспечение заданного β(β-величина, обратная постоянной времени).

Так как , то .

Задано β=18,00, тогда С₁= ≈1,59мкФ

Обеспечение равенства сопротивлений по обоим входам операционного усилителя. Для отсутствия у входа нуля операционных усилителей при некоторой асимметрии их по входу рекомендуется активные сопротивления, подключенные к обоим входам усилителя, выполнять равными. Т.к. в схеме пропорционально-интегрального регулятора сопротивление к входу «минус» определяется суммой R_вн+R₁, соединённых параллельно сопротивлению R₂, то сопротивление R₃, присоединенное к входу «плюс» вычисляется по формуле:

R₃= ≈5090,89 Ом

В 6 пункте задания предложено сравнить значения параметров идеальной и реальной (фактической) схем: коэффициентов усиления и значения входного и выходного сопротивлений схемы. Запишем формулу реального значения схемы, а именно коэффициента α:

1. α= 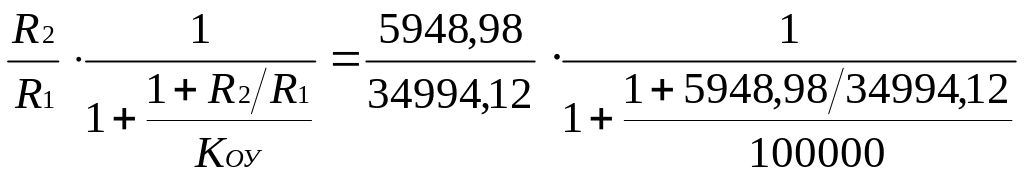≈0,169

Схема рассчитывается на усилителе К140УД12, подставив все данные, получим:

2. R_вх1= ≈34994,06 Ом

3. ≈0,0117 Ом

Параметры	Идеальные	Фактические
α	0,17	0,169
Rвх1	34994,12	34994,06
Rвых1	0	0,0117

Выясним, чем определяется передаточная функция звена с операционным усилителем. Рассмотрим схему с операционным усилителем в общем виде, используя упомянутые ранее допущения.

Так как можно считать что I ^'_вх ≈0, то I_ос=I_вх. Этот ток I_вх запишем в изображение:

I_вх(р)= , также ;

Поэтому , следовательно:

приравнивая I_oc=I_вх получим .

Отсюда - это идеальное выражение для передаточной функции. Реальное же изображение осложнено следующей дробью

, где Z_вх - сопротивление источника питания.

Учитывая заданную формулу напряжения U_вых1, запишем ее в изображениях:

, отсюда передаточная функция имеет вид:

.

Из предыдущего очевидно, что , , где .

Подставив вместо , получим выражение для АФХ:

. Напомним, что , а, значит, получим:

. Как и любое комплексное число Wпи(jω) имеет действительные и мнимые части: , где ,а .

Найдем модуль АФХ: .

Фаза АФХ:

, т.к. функция tg – нечетная. Здесь ω – абсолютная частота. Введем понятие относительной частоты, понимая под ней отношение: , где Т – постоянная времени интегрирующей части звена.

T= (с).

ω_абс= (1/с).

С полученными выше цифрами, действительная и мнимая части равны:

Re , Im .

Используя Re и Im найдем модуль и фазу АФХ:

;

.

Задавая ряд относительных частот от 0,01 до 100, подсчитаем абсолютное значение частот и, подставляя их в формулы для расчета модуля и фазы АФХ, рассчитаем точки модуля и фазы: ω_абс, lgω_абс, |W(jω)|, 20lg|W(jω)|,φ(jω).Результаты вычислений сведем в таблицу:

ωотн	ωабс	lgωабс	|W(jω)|	20lg|W(jω)|	φ(jω)
0,01	0,1797	- 0,745	100,0001	40,000	-89,9032
0,05	0,8985	- 0,046	20,0007	26,021	-89,5160
0,1	1,797	0,254	10,0014	20,0013	-89,0320
0,5	8,985	0,953	2,0072	6,0519	-85,1709
1,0	17,97	1,254	1,0143	0,1237	-80,4094
5,0	89,85	1,953	0,2625	-11,6178	-49,8074
10,0	179,7	2,254	0,1972	-14,1005	-30,6181
30,0	539,1	2,731	0,1732	-15,2272	-11,1597
50,0	898,5	2,953	0,1712	-15,3313	-6,7504
100,0	1797	3,254	0,1703	-15,3760	-3,8700

По данным таблицы построены ЛАЧХ и ЛФЧХ (стр. 9).

Правильность построения ЛАЧХ можно оценить по правилу, что при ω_сопр=100 (1/с) φ(ω_сопр)=-45º.