3.2 Гармонический анализ тока в программной среде MathCad

Все расчеты введем в системе СИ

Определим период колебаний основной гармоники:

Шаг интегрирования:

Количество точек за период: ,

Постоянная составляющая: ,

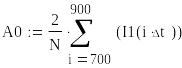Количество гармоник: ,

Определяем коэффициент a_n:

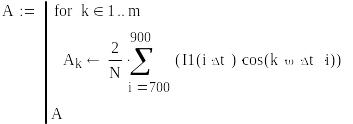
Определяем коэффициент b_n:

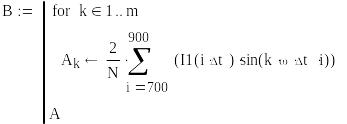
Отобразим найденные коэффициенты:

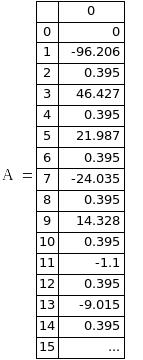
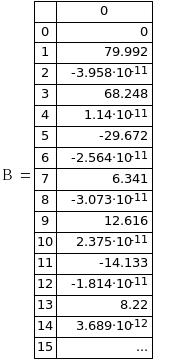
Строим спектр гармоник:

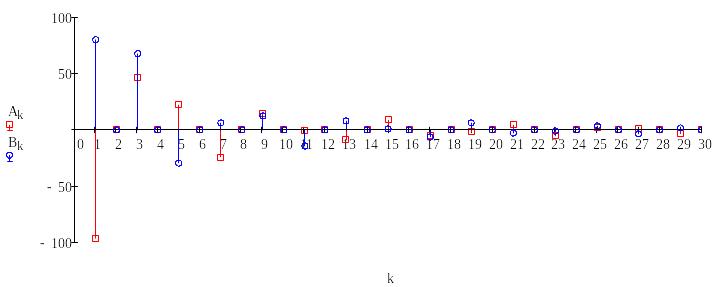
Рисунок 10 – Спектр гармоник по синусам и косинусам

Построим амплитудный спектр гармоник

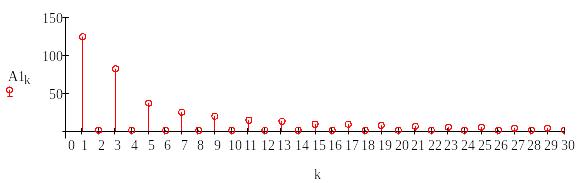
Рисунок 11 – Амплитудный спектр гармоник

По рисунку 11 видно, что преобладающими гармониками являются 1, 3, 5, 7, 9, 11, т.е. нечетные гармоники

Рассчитаем конечный гармонический ряд

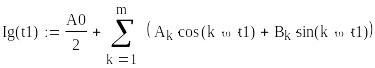
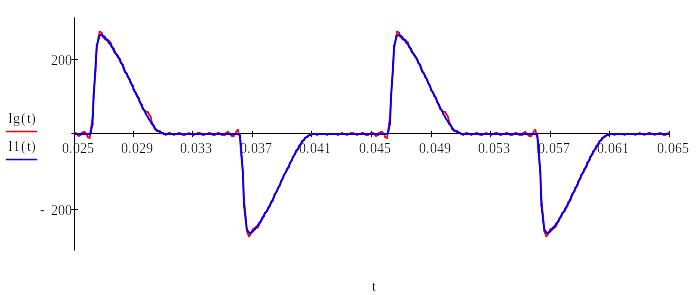
Рисунок 12 – Конечный гармонический ряд и исходная кривая

Рассчитаем среднеквадратичную ошибку

Как видно по результату, значение среднеквадратичной ошибки очень мала, 3,762%

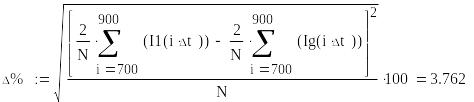
Построим график изменения среднеквадратичной ошибки

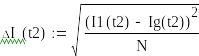
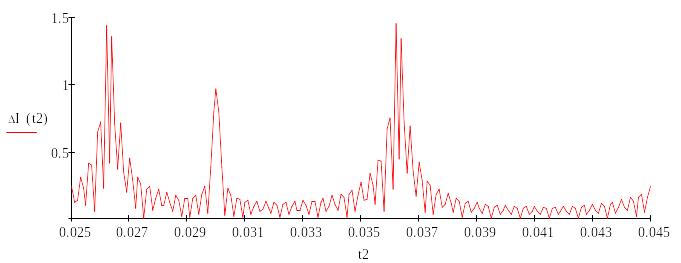
Рисунок 13 – График изменения среднеквадратичной ошибки

Вывод

Был рассмотрен метод интерполяции каноническими полиномами. Используя этот метод, была подвержена интерполяции основная кривая намагничивания, которая задана таблично. С помощью этой интерполяции была найдена зависимость Н(В).

Для решения дифференциального уравнения был использован метод Рунге-Кутта второго порядка с половинным шагом. Этот метод позволил построить переходной процесс тока нелинейной цепи. Была определена время переходного процесса методом дихотомии из разностного уравнения.

Анализ гармонического состава тока в цепи показал что не нулевыми гармониками оказались нечетные гармоники.

Список литературы

1. http://www.enin.tpu.ru/lib/EPEO_MSPD_1.swf.

2. Глазырин А.С. Математическое моделирование электромеханических систем. Аналитические методы: учебное пособие / А.С. Глазырин; Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2011. – 206 с..

3. Мальцева, Ольга Павловна. Численные методы в электротехнике: Компьютерный лабораторный практикум / О. П. Мальцева, Н. В. Коян, Л. С. Удут; Томский политехнический университет (ТПУ). – Томск: Изд-во ТПУ, 2003. – 99 с.: ил. – (Учебники Томского политехнического университета). – Библиогр.: с. 97. – ISBN 5-98298-101-X.

4. http://model.exponenta.ru/electro/pz_04.htm.

Контрольный вопрос

Интерполяция функции кубическими сплайнами.

Кубический сплайн - это функция, которая:

- проходит через все заданные 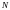точек , ;

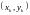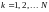- на каждом отрезке между соседними точками является кубическим полиномом;

- непрерывна вместе со своими первой и второй производными во всех точках.

Заметим, что, благодаря третьему условию, кубическая парабола 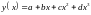через две точки проводится однозначно.

Формула для кубического сплайна записывается для произвольного отрезка с номером 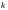, левый конец которого имеет абсциссу 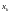. На этом отрезке для любого 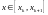результат интерполяции вычисляется по кубическому сплайну.

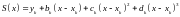(1)

Причем между заданными точками имеем 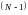отрезок, так что в этой формуле .

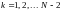Если переходит на другой отрезок, то следует изменить номер текущего отрезка и при этом изменятся все коэффициенты в формуле. На основании трех условий можно показать, что

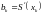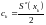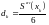, , (2)

где штрих означает дифференцирование по . Следовательно, коэффициенты сплайна характеризуют значения его производных в узлах интерполяции. Третья производная сплайна является разрывной функцией, но в задачах моделирования третьи производные используются очень редко.

Для проведения интерполяции, т.е. вычисления 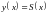для любого , предварительно по заданным точкам должны быть вычислены все коэффициенты сплайна, т.е. массивы 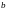, , 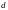каждый из которых имеет длину в соответствии с количеством отрезков между точками.

Постановка задачи: даны точек 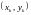, . Определить все коэффициенты сплайна 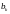, , 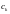, 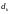т.е. всего 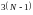коэффициентов, 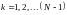, т.к. отрезок.

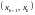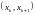Рассмотрим два любых соседних отрезка и с номерами 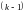и . Точка для них является общей.

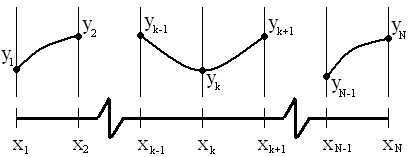
Рисунок 14 – Кубический сплайн

Для правого отрезка кубический сплайн имеет вид (1), а для левого, т.е. при

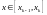
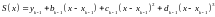(3)

.

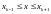В общей точке 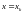приравняем левые и правые значения 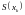и производных 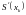и 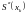в соответствии с определением кубического сплайна. Используя обозначение 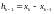для длины левого отрезка, получаем три уравнения для пяти неизвестных коэффициентов , , , , .

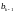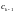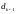Такие тройки уравнений можно записать для всех внутренних узлов , 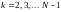, что даёт 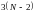уравнений.

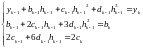(4)

(здесь это номера участков).

Ещё одно уравнение получаем, записывая для последнего узла 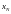первое из условий

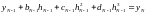(5)

В результате получаем 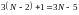уравнений. Эти уравнения содержат 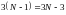неизвестных, т.к. для каждого отрезка между узлами имеем 3 неизвестных. Очевидно, что для однозначного определения коэффициентов нужны ещё два уравнения.

Эти дополнительные два уравнения могут быть произвольными, но обычно полагают, что функция 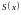вблизи её концов является линейной

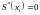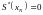и (6)

откуда 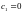, 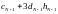=0

В результате введения двух дополнительных условий получается система уравнений с неизвестными коэффициентами , , . Эти уравнения можно преобразовать, выразив коэффициенты и через . Введем формально 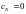. Тогда, имеем из последнего и первого уравнений (4) и уравнения (5):

,

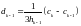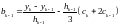, (7)

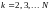
Подставляя эти выражения во второе уравнение (2.4), получим СЛАУ для коэффициентов :

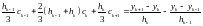(8)

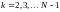, при , .

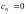В результате система из 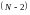линейных уравнений для неизвестных коэффициентов 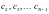. Матрица системы (8) состоит, в основном, из нулей и имеет только три ненулевых диагонали, а поэтому для её решения применяют не метод Гаусса, а специальный эффективный метод прогонки, резко сокращающий количество операций.

Часто систему уравнений (8) записывают для вторых производных в узлах, обозначая их 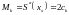. Тогда она принимает вид (Бахвалов, Численные методы, М., 2002):

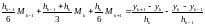(9)

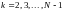, причем 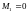и формально введено .
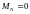