
- •Министерство образования и науки российской федерации
- •Национальный исследовательский томский политехнический университет
- •1. Интерполяция кривой намагничивания
- •1.1 Интерполяция каноническим полиномом
- •1.2 Интерполяция каноническими полиномами в программной среде MathCad 14
- •2. Расчёт переходного и установившегося процессов в цепи
- •2.1 Метод Рунге-Кутта второго порядка с половинным шагом
- •2.2 Расчёт переходного и установившегося процессов в цепи с применением метода Рунге-Кутта второго порядка с половинным шагом в программной среде MathCad
- •3. Анализ гармонического состава тока нелинейной цепи в установившемся режиме
- •3.1 Разложение в ряд в Фурье
- •3.2 Гармонический анализ тока в программной среде MathCad
- •Список литературы
- •Контрольный вопрос
2.1 Метод Рунге-Кутта второго порядка с половинным шагом
Методы Рунге-Кутта второго порядка основаны на разложении функции y(x) в ряд Тейлора и учете трех его первых членов (до второй производной включительно)
Формула метода Рунге-Кутта второго порядка с половинным шагом
имеет вид
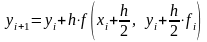 (2.3)
(2.3)
Геометрическая интерпретация метода (рисунок 4) заключается в следующем:
1.
Делают пробный шаг
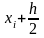 по
формуле Эйлера находят
по
формуле Эйлера находят
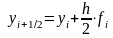
2. В найденной точке определяют наклон интегральной кривой

3. По этому наклону определяют приращение функции на следующем шаге
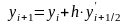
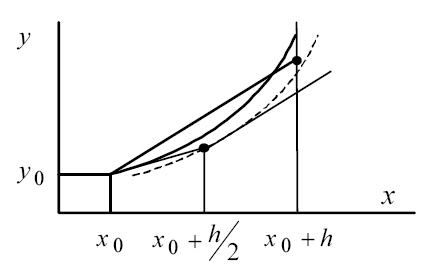
Рисунок 5 – Метод Рунге-Кутта второго порядка с половинным шагом
Алгоритм метода Рунге-Кутта с половинным шагом приведен на рисунке 6.
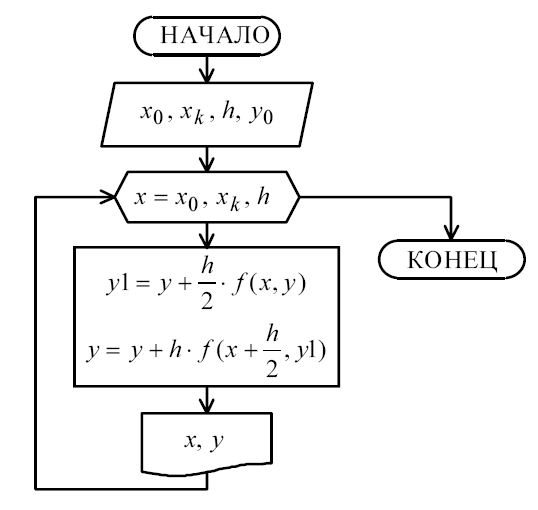
Рисунок 6 – Блок-схема алгоритма метода Рунге-Кутта второго порядка с половинным шагом
2.2 Расчёт переходного и установившегося процессов в цепи с применением метода Рунге-Кутта второго порядка с половинным шагом в программной среде MathCad
Все расчеты приведены в системе СИ
Параметры
катушки:
![]()
![]()
![]()
![]()
Параметры
сети:
![]()
![]() ;
;
Входное
воздействие:
![]() ;
;
Шаг
интегрирования:
![]()
Правая часть дифференциального уравнения:
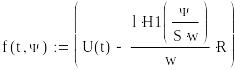
Начальные
условия:
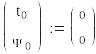
Задания
цикла:
![]()
Расчетное выражение:
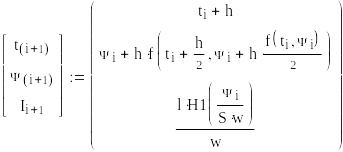
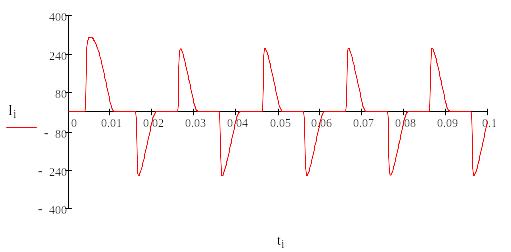
Рисунок 7 – График переходного процесса в цепи
Для такого чтоб привести ток Ii в зависимость I(t) проведем интерполяцию кубическим сплайном данной кривой:
![]()
![]()
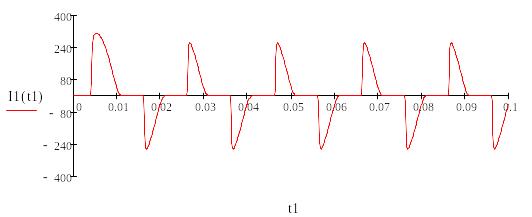
Рисунок 8 – График зависимости тока от времени I1(t1)
Определим уровень установившегося режима
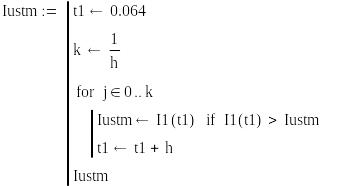
![]() А.
А.
Составим нелинейное уравнение. Учитываем 5% погрешность от шумов
![]()
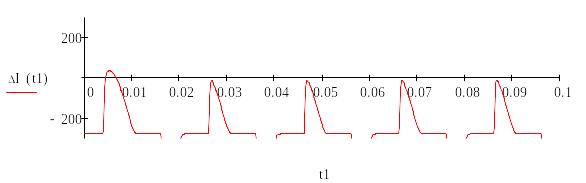
Рисунок 9 – График нелинейного уравнения
По рисунку 9 видно, что переходной процесс заканчивается до 0,01 с.
Определим время переходного процесса методом дихотомии
![]()

Время
переходного процесса:
![]() с.
с.
3. Анализ гармонического состава тока нелинейной цепи в установившемся режиме
В п. 2 после решения ДУ (2.2) было найдено время переходного процесса в нелинейной электрической цепи. Гармонический анализ следует проводить в установившемся режиме после окончания переходного процесса.
Указание: при разложении тока на гармоники следует брать интервал времени равный или кратный целому числу колебаний.
3.1 Разложение в ряд в Фурье
Разновидность обработки данных, связанная с преобразованием их частотного представления или спектра. Спектр получается в результате разложения исходной функции, зависящей от времени (временной ряд) или пространственных координат (например, изображения), в базис некоторой периодической функции. Наиболее часто для спектральной обработки используется спектр Фурье, получаемый на основе базиса синуса (разложение Фурье, преобразование Фурье).
Основной смысл преобразования Фурье в том, что исходная непериодическая функция произвольной формы, которую невозможно описать аналитически и в общем случае трудная для обработки и анализа, представляется в виде совокупности синусов или косинусов с различной частотой и амплитудой. Иными словами, сложная функция преобразуется в множество более простых. Каждая синусоида (или косинусоида) с определенной частотой и амплитудой, полученная в результате разложения Фурье, называется спектральной составляющей или гармоникой. Спектральные составляющие образуют спектр Фурье.
Тригонометрическим
рядом Фурье функции  называют
функциональный ряд вида
называют
функциональный ряд вида
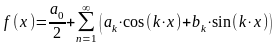 (3.1)
(3.1)
где
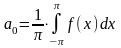 или
или
 ,
,
 или
или
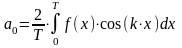 ,
,
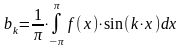 или
или
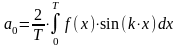 ,
,
Числа , (
, (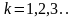 )
называются коэффициентами
Фурье функции f.
T
– период
гармонической функции.
)
называются коэффициентами
Фурье функции f.
T
– период
гармонической функции.
В нашем случае зависимость I(t) не является тригонометрической функцией и следовательно вычислить определенный интеграл будет не возможно. Для определения коэффициентов ряда Фурье, заменим интеграл суммой:
 ,
(3.2)
,
(3.2)
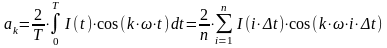 ,
(3.3)
,
(3.3)
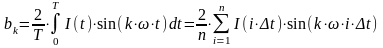 ,
(3.4)
,
(3.4)
где
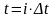 ,
,
 ,
,
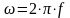 – частота основной гармоники.
– частота основной гармоники.
