Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«Пермский национальный исследовательский политехнический университет»

Кафедра Автоматизации технологических процессов и производств

Отчет по лабораторной работе № 2

Моделирование теплообменных аппаратов

(название лабораторной работы)

Выполнил
студент гр.	КСК-09
		Кривелев Ф.С.
(подпись)		(Ф.И.О.)
Проверил преподаватель
		Вялых И.А.
(подпись)		(Ф.И.О.)

Пермь 2012

1. Цель работы

Получение практических навыков математического моделирования тепловых процессов, построение моделей теплообменных аппаратов, исследование на моделях различных статических режимов работы теплообменных аппаратов, их оптимизация.

2. Теоретические сведения

Теплообменные процессы широко распространены химической технологии. Теплообменные процессы протекают с передачей тепла от более нагретого вещества (теплоносителя) к менее нагретому (хладагенту). Аппараты для проведения таких процессов – теплообменники – различаются по способу передачи тепла: с контактом теплоносителя и хладагента; без контакта – с теплообменом через теплопередающую стенку. Теплообменники без контакта веществ являются наиболее распространёнными и среди них можно выделить следующие:

1. прямоточные;

2. противоточные;

3. с перекрёстным течением.

При построении математических моделей использованы следующие допущения:

1) потоки в аппарате описываются моделью идеального вытеснения:

; (1)

2) потери тепла не учитываются.

На рис. схематично показан прямоточный теплообменник.

Рисунок 1 - Схематическое изображение прямоточного теплообменника

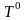‑ температура теплоносителя на входе, К;

‑ температура теплоносителя на выходе, К;

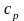‑ теплоёмкость теплоносителя, ;

‑ массовый расход теплоносителя, кг/с;

‑ температура хладагента на входе, К;

‑ температура хладагента на выходе, К;

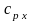‑ теплоёмкость хладагента, ;

‑ массовый расход хладагента, кг/с.

Распределение температуры по длине аппарата в установившемся режиме схематично представлено на рис.2.

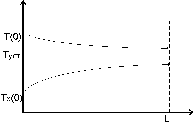
Рисунок 2 - Распределение температуры по длине аппарата

На рис.2 видно что, температура теплоносителя понижается (остывает), а хладагента – повышается (нагревается). При бесконечной длине аппарата обе температуры должны сравняться и приблизиться к значению Т_уст.

Для противоточного теплообменника схема подачи потоков изображена на рис.3, а распределение температуры по длине аппарата в установившемся режиме – на рис.4.

Рисунок 3 - Схематическое изображение противоточного теплообменника

Теплоноситель и хладагент подаются навстречу друг другу.

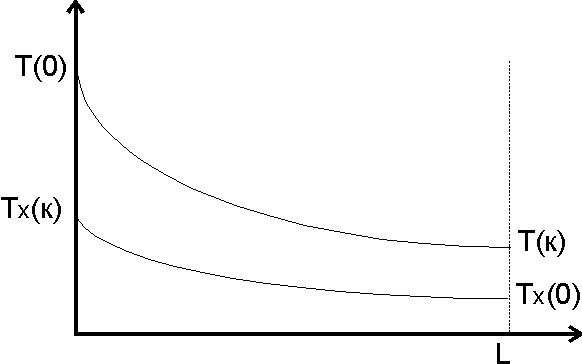
Рисунок 4 - Распределение температуры по длине аппарата

На рис.4 видно, что теплоноситель остывает до определённой температуры, а хладагент – нагревается.

Система дифференциальных уравнений динамики процесса для прямоточного теплообменника имеет вид

(2)

где ‑ поверхность теплообмена, м²;

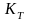‑ коэффициент теплопередачи, ;

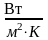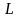‑ длина аппарата, м;

‑ текущий линейный размер, м;

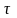‑ астрономическое время, с;

– объемные расходы теплоносителя и хладоагента соответственно, ;

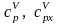– удельные объемные теплоемкости теплоносителя и хладагента соответственно, .

Подставим в (2) выражения связи удельной массовой теплоемкости с удельной объемной теплоемкостью 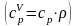и объемного расхода с массовым расходом :

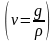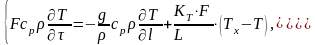(3)

Разделим первое и второе уравнения (3) на и соответственно. Получим

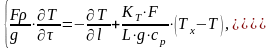(2.4)

Для противоточного теплообменника:

(2.5)

Для установившегося режима работы теплообменника и . Следовательно, (4) и (5) примут вид

(2.6)

(2.7)

Расчет оптимального расхода хладагента и поверхности теплообмена для теплообменника прямоточного типа

В данном случае зависимость поверхности теплообмена 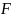от расхода хладагента описывается выражением:

, (2.8)

где

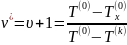; (2.9)

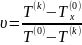. (2.10)

Условие, которому должно удовлетворять оптимальное значение нагрузки по хладагенту:

. (2.11)

Уравнение (11) может быть приведено к виду:

, (2.12)

где

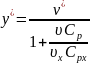. (2.13)

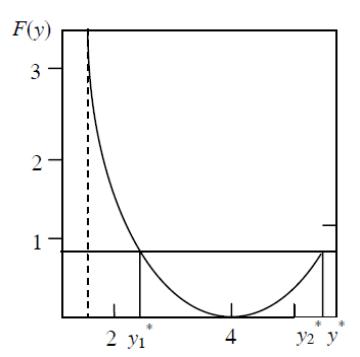
Рисунок 5 – Определение оптимальных параметров теплообменников прямоточного типа

Найденное значение используется для расчета оптимальных значений нагрузки теплообменника по хладагенту и поверхности теплообмена по формулам:

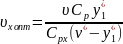, (14)

. (15)

3. Расчетно-графическая часть

3.1. Исходные данные

Вариант №5

3.1.1. Для расчета расхода и конечной температуры хладагента:

;

;

;

;

;

;

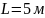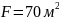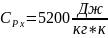Для прямотока:

;

;

.

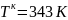Для противотока:

;

;

.

3.1.2. Для расчета оптимальных расхода и поверхности теплообмена для прямоточного теплообменника:

Значение отношения стоимости теплообмена:

;

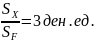Значения плотности горячего теплоносителя и хладагента соответственно равны:

;

.

3.2. Расчетная часть

3.2.1. Расчет расхода хладагента для прямоточного теплообменника и конечной температуры хладагента для противоточного теплообменника:

Расчет расхода хладагента производится по системе дифференциальных уравнений согласно (2.6):

. (3.1)

Начальными условиями для системы (3.1.) являются начальные температуры для теплоносителя и хладагента:

; (3.1а)

. (3.1б)

График изменения температуры хладагента и теплоносителя для прямоточного теплообменника представлен на рис. 6.

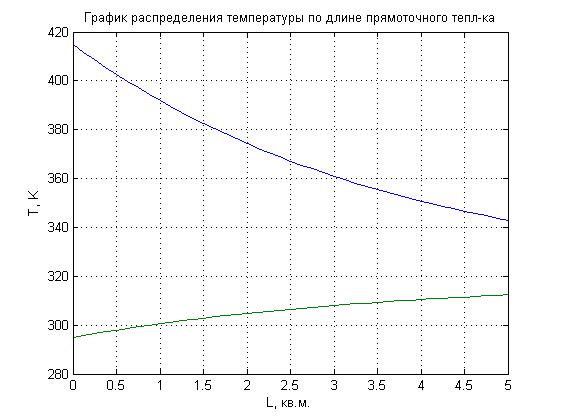
Рисунок 6 - График изменения температуры хладагента и теплоносителя для прямоточного теплообменника

Расчет конечной температуры хладагента для противоточного теплообменника:

. (3.2)

Начальными условиями для системы (3.2) являются начальные температуры для теплоносителя и хладагента:

; (3.2а)

. (3.2б)

График изменения температуры хладагента и теплоносителя для противоточного теплообменника представлен на рис. 7.

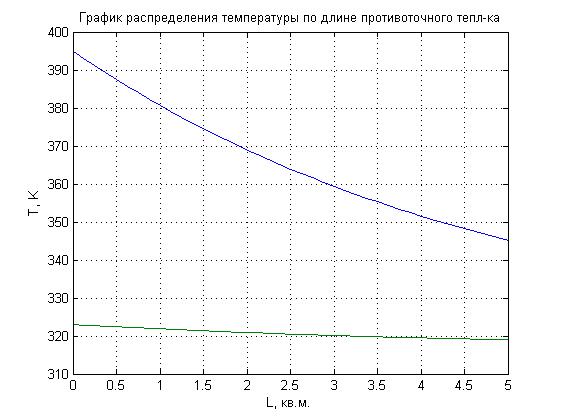
Рисунок 7 - График изменения температуры хладагента и теплоносителя для противоточного теплообменника

Программа расчета представлена в приложении, полученные данные сведены в таблицы 1, 2.