20. Индексы цепные и базисные, с постоянной и переменной базой сравнения.

Индексы могут быть использованы для анализа динамики социально-экономических явлений за ряд последовательных периодов. В этом случае различаются базисные и цепные индексы.

Базисные индексы используются для наглядной характеристики общей тенденции развития исследуемого явления. Цепные индексы – последовательного изменения уровней в объеме.

Между цепными и базисными индексами существует взаимосвязь:

1. если известны цепные индексы 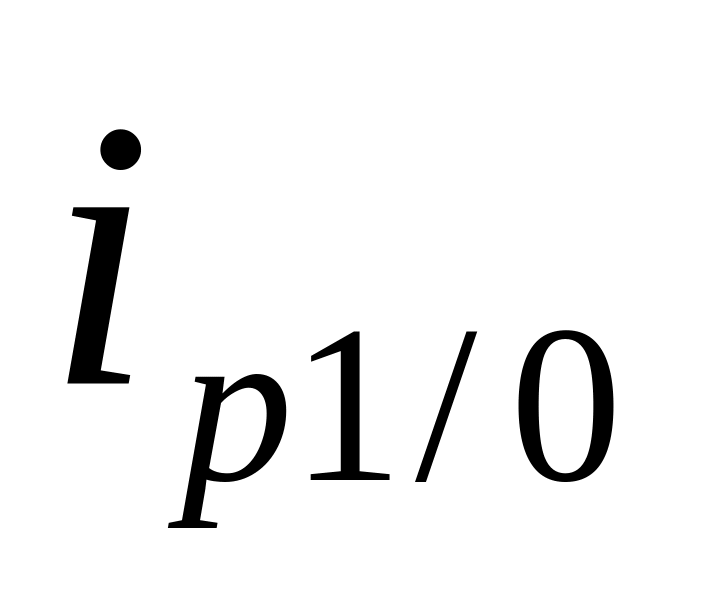, , - перемножить эти индексы

2. если известны базисные индексы , , 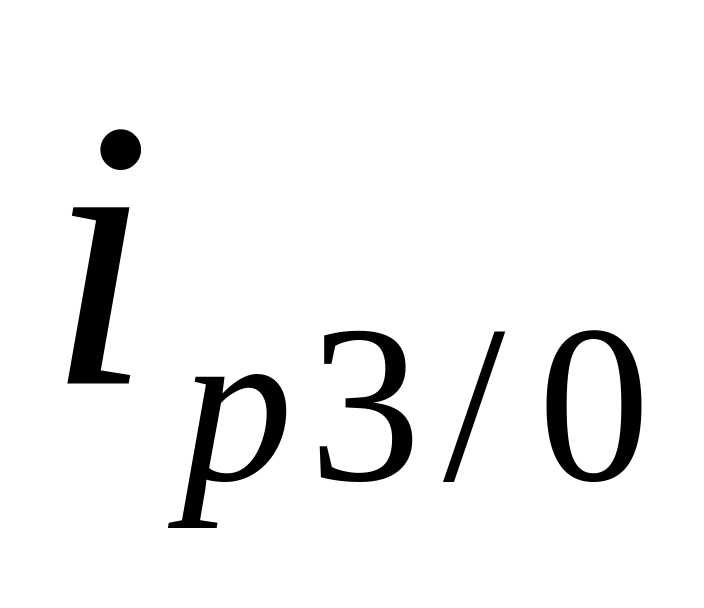- разделить их один на другой , .

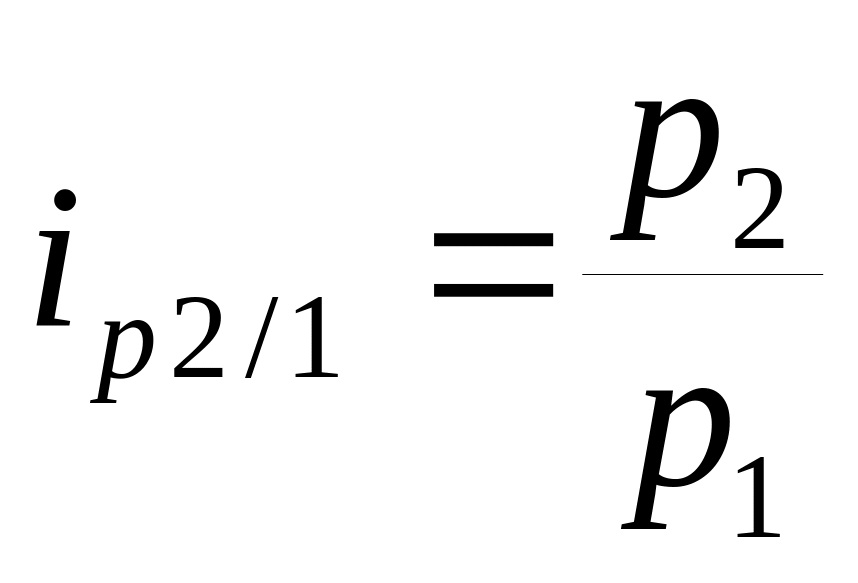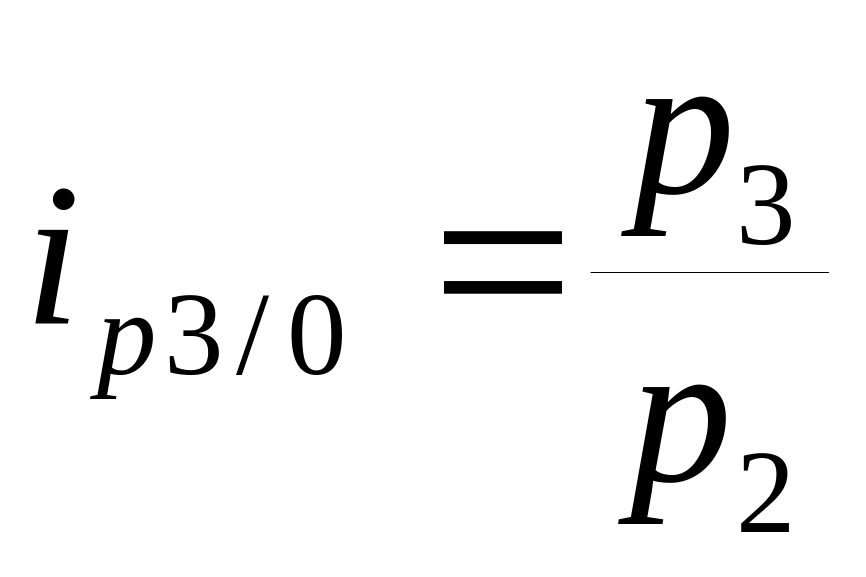Аналогично рассчитываются индексы общие.

При построении системы индексов можно использовать индексы с постоянными и переменными весами

Системы индексов с постоянными весами называется системой общих индексов одного и того же явления (р или q), вычисленная с весами, не меняющимися при переходе от одного индекса к другому.

Постоянные веса позволяют исключить влияние изменения структуры на величину индекса.

Например для индекса физического объема

- построим систему базисных индексов с постоянными весами: ;

- построим систему цепных индексов с постоянными весами: .

Система индексов с переменными весами- это система общих индексов одного и того же явления , вычисленных с весами, которые меняются от одного индекса к другому. Переменные веса- веса отчетного периода.

- построим систему цепных индексов с переменными весами: ;

- построим систему базисных индексов с переменными весами: .

21. Индексы средних величин (индексы переменного, постоянного состава и структурных сдвигов).

Индексы средние применяются, когда на разных предприятиях производится или продается одна и та же продукция. Для того чтобы сравнить объемы продаж необходимо сравнить средние цены на данный вид продукции. Анализ полученных показателей производят при помощи ср. индексов.

1. Индекс переменного состава - изменение средней цены на продукцию под влиянием 2-х факторов в текущем и в базисном периоде в среднем по всем предприятиям. ; .

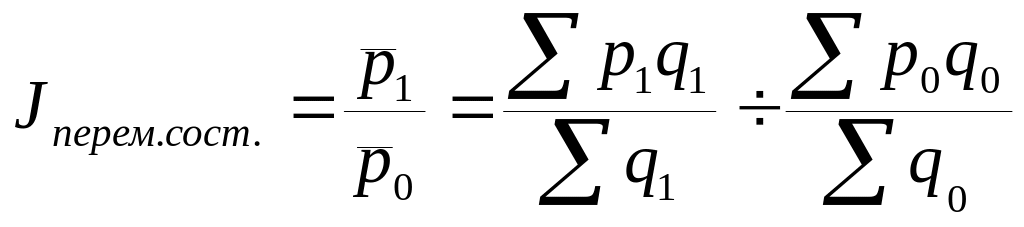2. Индекс постоянного состава Он показывает на сколько изменится средняя цена на продукцию за счет изменения цены на каждом предприятии. ; .

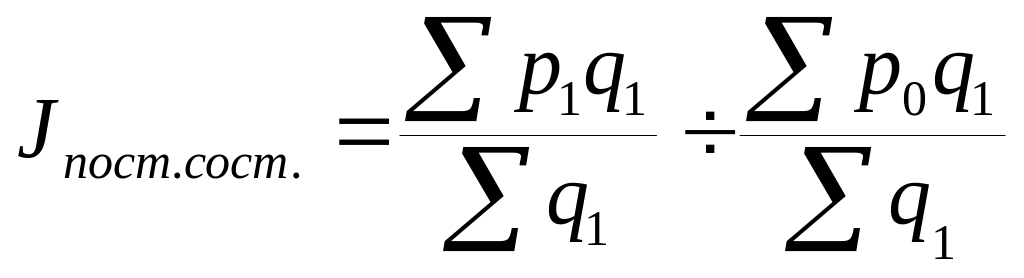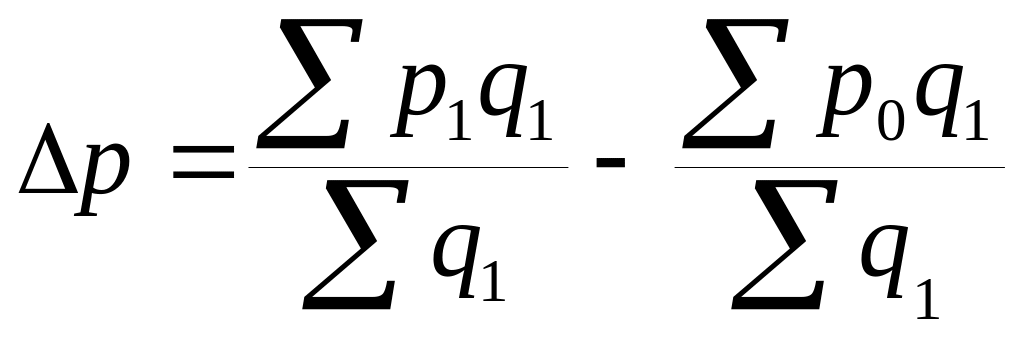3. Индекс структурных сдвигов В этом случае изменение средней цены происходит за счет изменения объема продаж продукции на каждом предприятии. ; .

Взаимосвязь индексов

или

22. Территориальные индексы.

Особенность данных индексов является то, то при двух стороннем сравнении каждый регион может быть принят в качестве сравниваемого, так и в качестве базы сравнения.

При определении общих индексов будет меняться база сравнения. Например:

- для индекса физического объема. Если сравнивают города К и М, то в качестве базы сравненя будет выступать цена в городе К , затем .

- для индекса цены. В качестве базы сравнения , .

Рассмотрим территориальные индексы, если в качестве базы сравнения будет выбран город К.

- база сравнения г. К ;

- база сравнения г. М .

Если известны данные на одноименный вид товара в 2-х городах, то общий индекс цены может быть рассчитан следующим образом: , .

Для индексов физического объема в качестве веса соизмерителя может выступать средняя цена на одноименную продукцию , где - цена продукции в каждом регионе, - количество произведенной продукции в каждом регионе.